02 АЗЭ Лекционный материал / лекция 9

Обратим внимание, что пределы (9.16) должен существовать в каждом узле «р» сети. Численная реализация определение сходимости требует оцен-

ки и сравнения значений узловых напряжений токов и мощностей на теку-

щих итерациях. При этом возможно улучшение или ухудшение качества ре-

шений, что определяет сходящийся или расходящийся процесс. Кроме того, и

для того и для другого случая характерно апериодический или колебатель-

ный характер процесса.

В практике применение итерационных методов принято считать оценку качества решений по изменению узловых напряжений косвенной а по узло-

вым небалансам токов и мощностей прямой они соответственно определяют необходимые и достаточные условия сходимости. В необходимых условиях на каждом шаге, в каждом узле производиться оценка величины приращения узлового напряжения.

По абсолютной величине:

(U1ip U1(pi 1) )2 (U 2ip U 2(pi 1)			εΔU	(9.17)
(U ip U ip 1) εΔU				(9.18)
( ip	i 1)	ε		(9.19)
	p	Δδ

р = 1,2,3,…n U= 1,2,3,….

Здесь величина ε с соответствующими индексами, заданными до начала расчета погрешности по приращению напряжений в узлах по модулю и фазе.

Оценка в форме (9.17) не удобна из-за большого количества операций, по-

этому в место неё часто используется:

U1ip				U1ip 1		εΔU	(9.20)

U2ip U2ip 1 εΔU

р = 1,2,3,…n

U= 1,2,3,….

Недостаток оценок (9.17)-(9.19) состоит в том, что они проводятся после вычисленных новых значений узлового напряжения в каждом узле при этом рассматриваемое условие сходимости считается выполненным если оценки

(9.17)-(9.20) дали положительные ответы во всех узлах. Если хотя бы в одном узле ответ отрицательный то, следовательно, отрицательна и вся оценка, по-

этому более эффективная как показала практика расчетов является не анали-

тическая оценка.

n
(	U1 ip		U2 ip	) ε U Σ	(9.21)
p 1

где

U1i		U1i				U1i 1
p		p				p

U2 i		U2 i				U2 i 1
p		p				p

Для этой наиболее эффективной оценки производится последовательный набор суммы модулей приращений вещественных и мнимых составляющих узловых напряжений и сравнение этой суммы с общей погрешностью εΔUΣ

имеющая формальный смысл.

Выполнение необходимых условий сходимости в виде (9.17)-(9.20) гаран-

тирует только малую величину приращения. Для окончательного ответа о ка-

честве решения необходима проверка достаточных условий.

Для этого квадратичные неотрицательные суммы составляющих узловых небалансов по току и мощности определяется в виде численных значений функционалов:

	(и)	n
I ( U )	( I1p2		I2 p2 ) ε φI	(9.22)
	p 1
(и)	n
φ S (U	) ( Pp2		Qp2 ) ε φΔЅ	(9.23)

p 1

Оценки качества условия (9.22) и (9.23) является абсолютными и оконча-

тельными. По существу они оценивают длину векторов узловых небалансов по току и мощности в 2n мерном пространстве координатами которого явля-

ется составляющие вектора узловых и в виде U1,U2 или U и δ.

Более удобнее эти координаты и вектора узловых небалансов записыва-

ются в 2n мерной форме в виде

U1		I1
X		WI	(9.24)
U2		I2

			W S		P
X						(9.25)
U					Q
		2n
в этом случае φI = φ (Ui ) w I2
		k 1	k
			i 2n
		φΔS =	(U ) ws2			(9.26)
			k 1	k

Выбор оптимального шага при решении уравнений установившегося ре-

жима электрической сети.

При анализе установившихся режимов электрических сетей с помощью метода наискорейшего спуска рассматривается функционал токов небаланса

n	n
I1i2	I 2i2 , где I1 и I2 – соответственно действительные и мнимые
i 1	i 1

составляющие значений узловых токов небаланса; n – число независимых уз-

лов схемы.

Решение системы нелинейных уравнений X U2U1 – вектор размерностью

2n, где U1 и U2 – соответственно векторы действительных и мнимых частей значений узловых напряжений, отыскивается как координаты точки экстре-

мума функционала φ в пространстве размерностью 2n: X 0 .

Для этого на каждом шаге итерационного процесса, зная некоторые зна-

чения вектора X, находят новые значения составляющих этого вектора, отве-

чающие меньшему, чем исходные значению функционала φ, по следующему выражению:

t tп

		Xi 1	Xi t gradX ,	(9.27)
где grad	X		– вектор-градиент токов небаланса, получаемый диффе-
		X

ренцированием функционала φ по всем составляющим вектора X; t – шаг в направлении вектора-антиградиента, который соответствует направлению обобщенной касательной к поверхности функционала φ в точке Xi простран-

ства размерностью 2n; i 1 – номер итерации.

При реализации алгоритма расчета установившегося режима методом наискорейшего спуска возникают две задачи:

1)определение вектора-градиента X ,

2)определение оптимальной величины шага t. Остановимся подробнее на вопросе выбора шага t. Обозначим пробный шаг tп .

Имея некоторые начальные значения неизвестных X0 , по выражению (1)

при можно получить новые значения неизвестных X1 . Будем считать наилучшим значением шага t , соответствующее минимуму φ по направле-

нию антиградиента:

		0 .
t
		t t

Значение уточняющего шага tу , удовлетворяющее этому условию, можно вычислить приближенно, приняв допущение о линейной зависимости произ-

водной функционала φ по направлению антиградиента от величины шага t

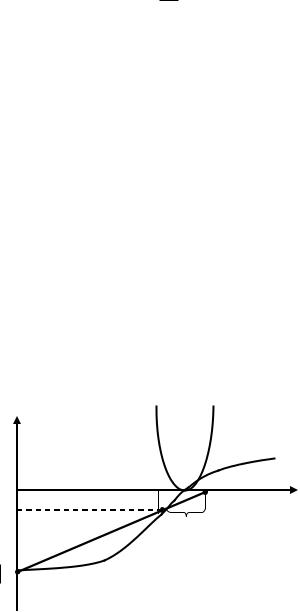
(рис. 9.2.).			,
						(t)
			t
				tп	t*		t
		t t
t		0n

tу

t t 0

(рис.9.2.).Зависимость производной функционала φ по направлению антиградиента

от величины шага t

Из подобия двух треугольников найдем уточняющий шаг

tу tп

,

(9.28)

t

t

t

t tп

t 0

t tп

где

и

– производные функционала φ по направлению антигра-

t

t 0

t

t tп

диента соответственно в начальной точке t 0

и при t tп .

Представим производную в виде

Х

. Дифференцируя основное

t

Х

t

итерационное выражение по t, получим:

Х

.

t

Х

t 0

Тогда выражения для производных в формуле (9.28) можно записать сле-

дующим образом:

Х

2

;

(9.29)

t

Х

t

Х

t 0

t 0

t 0

Х

т

(9.30)

t

t tп

Х

t tп

t

Х

t tп

Х

t 0

Каждое из полученных выражений представляет собой скалярное произ-

ведение двух векторов-градиентов с обратным знаком. Индекс “т” означает транспонирование первого из векторов-градиентов.

С учетом (9.29) и (9.30) выражение для нахождения уточняющего шага

(9.29) запишется следующим образом:

		После
ных X2 ,
		X
				t tп

т

2

т

t t

.

y

п

Х

t tп

Х

t 0

Х

t 0

Х

t tп

Х

t 0

вычисления шага ty можно определить новые значения неизвестпринимая в качестве направляющего вектор-антиградиент

, по следующему выражению:

Х2 Х1 t у				.
	X
			t tп

Таким образом, каждая итерация метода наискорейшего спуска состоит из двух частей – итерация с пробным шагом и итерация с уточняющим шагом