Министерство образования Российской Федерации. Государственное образовательное учреждение высшего профессионального образования

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра «МЕХАНИКА»

К О Л Е Б А Н И Я МАТЕРИАЛЬНОЙ ТОЧКИ

Данное пособие входит в серию электронных учебных пособий по теоретической механике, разрабатываемых на кафедре механики СамГТУ.

Пособие предназначено для самостоятельного изучения студентами темы «Колебания материальной точки».

Зав. кафедрой – д.т.н., проф. Я.М.Клебанов, Разработчики – Л.Б.Черняховская, Л.А.Шабанов.

Самара – 2007.

1. Свободные колебания материальной точки.

Пусть на материальную точку действует сила, прямо пропорциональная отклонению точки от положения равновесия и направленная в сторону, противоположную этому отклонению (рис.1).

Восстанавливающей называется сила, стремящаяся вернуть точку в положение равновесия:

F = −c OM ,

где с – коэффициент пропорциональности.

Направим ось х по линии действия силы, выбрав начало отсчета в положении равновесия точки. Проекция восстанавливающей силы на ось х равна Fx = −cx.

		В начальный момент					при t =0, координата точки x = х0,				начальная
	скорость		x = х0 .
			&	&
							Дифференциальное уравнение				движения
		О	F		М х		материальной точки под действием восстанавли-
			х				вающей силы имеет вид
								d 2 x
							m			= −cx .
			Рис.1					dt	2
				c			Разделим обе части этого уравнения на m,
	обозначим				= k 2 , в результате получим дифференциальное уравнение
				m

движения точки под действием восстанавливающей силы:

d 2 x		+ k	2	x = 0 ,	(1)
dt	2

Уравнение (1) – однородное линейное уравнение второго порядка. Для его решения запишем соответствующее характеристическое уравнение

r 2 − k 2 = 0 , корни которого r1,2 = ± ki.. Так как корни характеристического

уравнения r1 и r2 являются мнимыми, то решение уравнения (3.1) записывается в виде

x = C1 cos kt +C2 sin kt.

(2)

Это решение можно представить в виде:

x =аsin(kt +α).

(3)

Распишем синус суммы двух углов в уравнении (3) и получим

x = аcosαsin kt +asinαcos kt ,

Заменим a sinα, = С1 a cosα. = С2 , получим уравнение в форме (2).

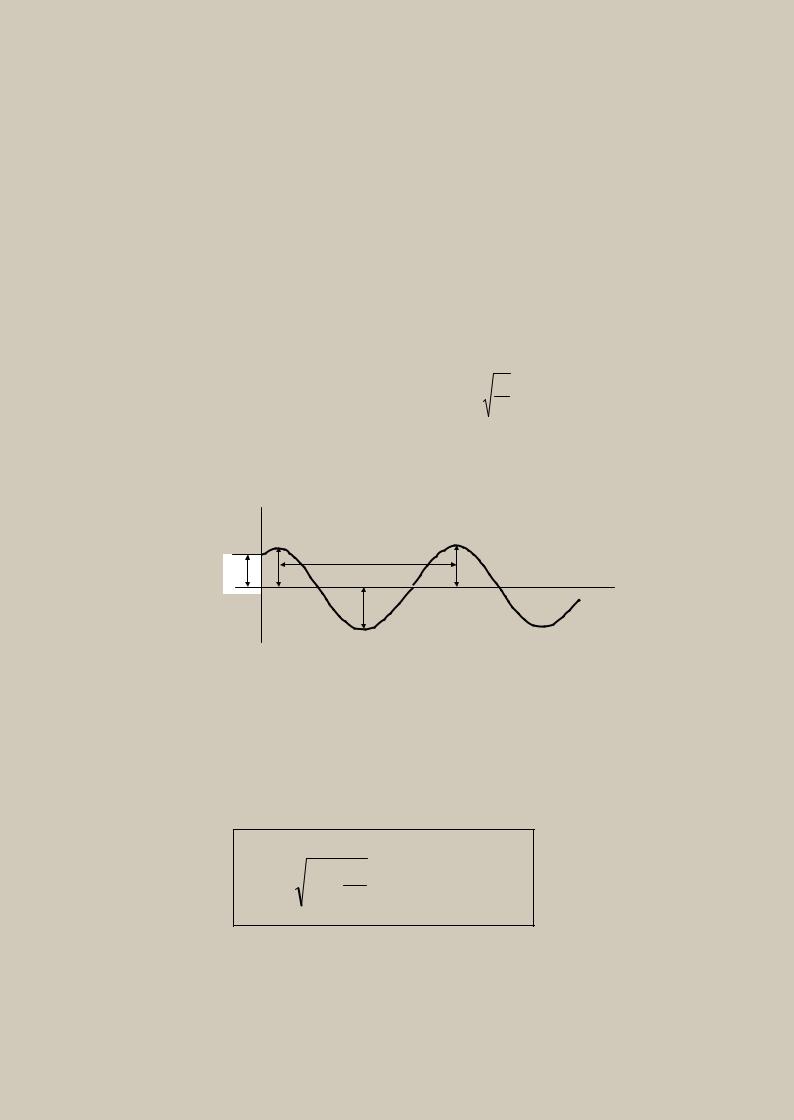
Таким образом, под действием восстанавливающей силы материальная точка совершает движение по синусоидальному закону:

x=аsin(kt+α).

Такое движение называется свободными гармоническими колебаниями материальной точки.

График гармонических колебаний показан на рис. 2.

Амплитудой колебаний называется максимальное отклонение точки от положения равновесия, равное а.

Фазой колебаний называется аргумент (kt+α), где α - начальная фаза.

Частота гармонических колебаний	k =	c .	(4)
		m

Определим амплитуду и начальную фазу колебаний. Скорость колебаний равна

		x = ak cos(kt +α) .		(5)
		&
		х
	х0		T
		а	а	t
		О	а
			Рис. 3.2
Подставим в уравнения (3) и (5) начальные условия:
t = 0, х = x0	, х = x0 ,		получим:
	&	&

x0 = asinα, x&0 = a k cosα.

Отсюда

	V 2	tgα =	kx0
a =	x02 + k02 ,			.	(6)
			V
			0

Таким образом, амплитуда и начальная фаза определяются начальными условиями движения точки

Периодом колебаний называется наименьший промежуток времени Т, по истечению которого движение точки полностью повторяется, т.е. точка

проходит одно и то же положение в одном и том же направлении, следова-
тельно, координаты точек по истечению времени Т совпадают:
			x = a sin( kt +α) = a sin( kt +T +α) .
Это равенство справедливо, если				kt +T +α =kt +α + 2π .
Следовательно, период колебаний равен
			T = 2π		(7)
			k
Откуда			k = 2Tπ .		(8)
Частота k			определяет число полных колебаний точки за время,
равное 2π секундам.
Частота k не зависит от начальных условий движения, поэтому ее назы-
вают собственной частотой гармонических колебаний
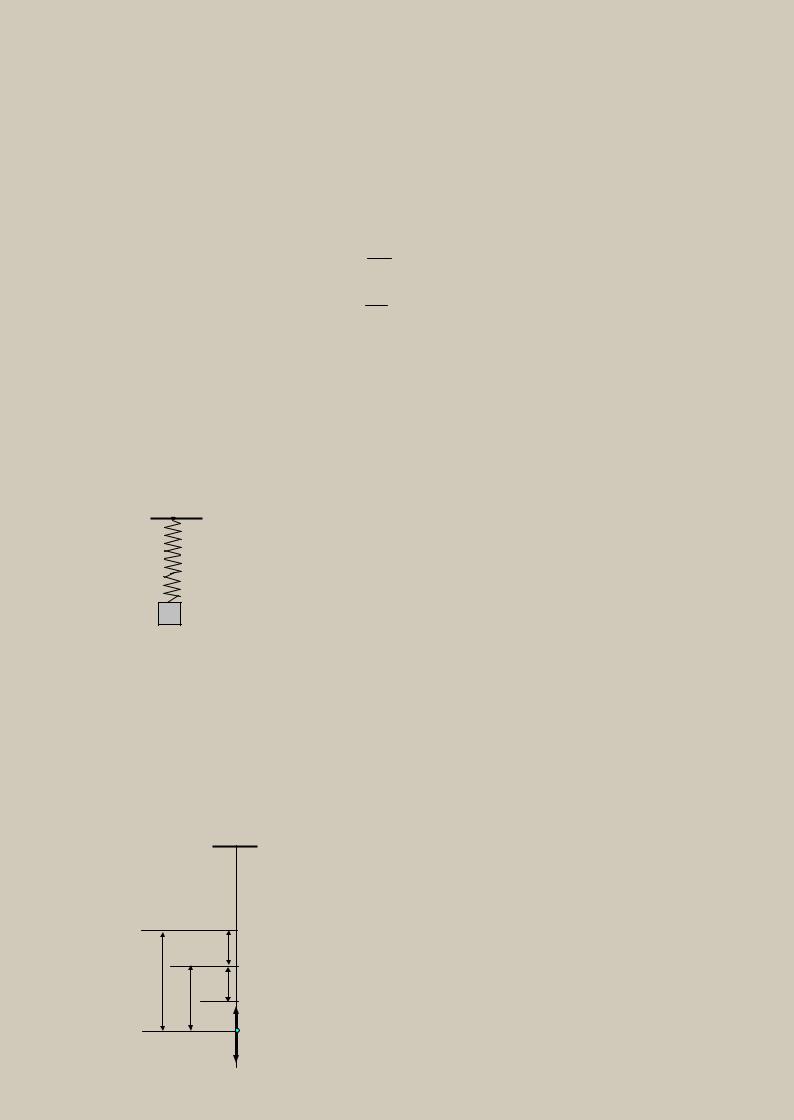
1.1. Колебания груза, подвешенного на пружине
			Рассмотрим движение груза, подвешенного на пружине,
		коэффициент жесткости которой равен с (рис.3).
			На груз, подвешенный на пружине, действуют сила тяже-
		сти и сила упругости пружины. Величина силы упругости, воз-
		никающей при деформации пружины, пропорциональна ее уд-
		линению λ:
Рис.3.			F = cλ.
Статическим λст называется				удлинение пружины, при котором груз
находится в равновесии. В данном случае сила упругости, равная Fст					= cλст ,
в положении равновесия уравновешивается силой тяжести: mg = cλст .
Отсюда статическое удлинение				λст = mg .	(9)
				с
Рассмотрим движение груза после того, как он был смещен из положе-
			ния равновесия и отпущен с начальной скоростью.
			Примем груз за материальную точку, направим
			ось х вертикально вниз, приняв за начало отсчета
			положение статического равновесия.
	ст		Пусть в начальный момент времени t = 0
	λ	О
			точка смещена из положения статического
λ х	0
	х	F	равновесия на величинух0 , а начальная ско-
				&
		М	рость равнах0 (рис.4).
		mg
	Рис.4

При отклонении груза М от положения статического равновесия на величину ОМ = х, полная деформация пружины равна λ = (λст + х), проекция силы упругости на ось х равна

Fх = −с (λст + х)

Движение точки происходит под действием двух сил: силы тяжести и восстанавливающей силы. Запишем дифференциальное уравнение для этого движения

	m	d 2 x	= mg −c (λст + x) .
		dt 2
	Подставим в это уравнение		значение с=	mg		, полученное из формулы
				λ
				ст

(9):

или

Заменим

m

d 2 x

= mg −

mg

(λст + x) = mg −mg −

mg

x .

dt 2

λст

λст

d

2 x

+

g

x = 0 .

dt 2

λст

k 2

=

g

,

получим дифференциальное уравнение свободных

λ

ст

гармонических колебаний:

d 2 x +k 2 x = 0 . dt 2

Решение этого уравнения:

x =аsin(kt+α).

Следовательно, движение груза, подвешенного на пружине, представляет собой свободные гармонические колебания относительно положения статического равновесия. Частота и период свободных колебаний груза опреде-

ляются по формулам (5) и (6), после подстановки в них значения

с =

mg

из

λ

формулы (9) получим

ст

k =

g

,

T

=

2π

= 2π

λст

.

λст

k

g

Амплитуда а и начальная фаза α зависят от начальных условий и опре-

деляются по формулам (6):

kx0

V

2

tgα =

a =

x02 + k02 ,

,

V

0

1.2. Примеры на свободные колебания

Пример 1.	Груз массой			m подвешен на двух последова-
тельно соединений пружинах				с различными коэффициентами				с1
жесткости c1 и с2 (рис.4). Определить частоту колебаний. по-								с2
следовательно соединенных пружинах полное статическое уд-
линение равно сумме удлинений двух пружин:
	λ = λ1ст +λ2ст .
							Рис.4
Статическое удлинение каждой пружины определяется форму-
лой (8):	λ1ст =	mg	,	λ2ст =	mg	.
		c1			c2

Полное статическое удлинение выражается через эквивалентный коэффициент жесткости двух пружин с, значит, λ = mgc .

Тогда

mg

=

mg

+

mg

или

1

=

1

+

1

, откуда

c =

c1 c2

c

c

c

c

c

c

+c

c

2

2

2

1

1

1

Частота колебаний

k =

c

=

c1 c2

.

m

m (c

+c

)

1

2

Пример 2. Определить эквивалентный коэффициент жесткости двух параллельно соединенных пружин с различными коэффициентами жесткости с1 и

с2.

с2		l2		l1			с1	При параллельном соединении пружин (рис.3.5) в
							положении статического равновесия результирующая
							сила упругости F = F1 +F2 ,
			Рис.5					Тогда:
							сλст =с1 λ1ст +с2 λ2ст.
		Результирующее удлинение и удлинения обеих пружин должны быть
одинаковы:						λст = λ1ст		= λ2ст.
		Следовательно,						с = с1 + с2 .

Кроме того, точка, к которой прикрепляется груз, должна удовлетворять условию равновесия, т.е. сумма моментов сил упругости относительно точки закрепления груза должна быть равна нулю: F1l1 − F2l2 = 0 .

Отсюда следует,

F1

=

l2

, или

с1λcn

=

l2

.

F

l

c

λ

cn

l

2

1

2

1

Окончательно,

l2

=

c1

, т.е. точка закрепления груза делит расстояние между пру-

l

c

2

1

жинами обратно пропорционально коэффициентам их жесткости.

	Пример 3. Определить частоту колебаний груза, подвешенного за-
	крепленного на двух пружинах с коэффициентами жесткости с1 и с2,
с1	как показано на рис. 6.
	В этом случае статические удлинения обеих пружин оди-
	наковы. Сила тяжести груза уравновешивается силами упруго-
с2	сти обеих пружин F1 = с1 λст и F2= с2 λст, значит
	mg = с1 λст + с2 λст = (c1 + c2) λст.

Рис.6	Отсюда эквивалентный коэффициент жесткости с = с1 + с2.
	Частота колебаний груза в этом случае равна
	k =	c =	c1 +c2 .
		m	m

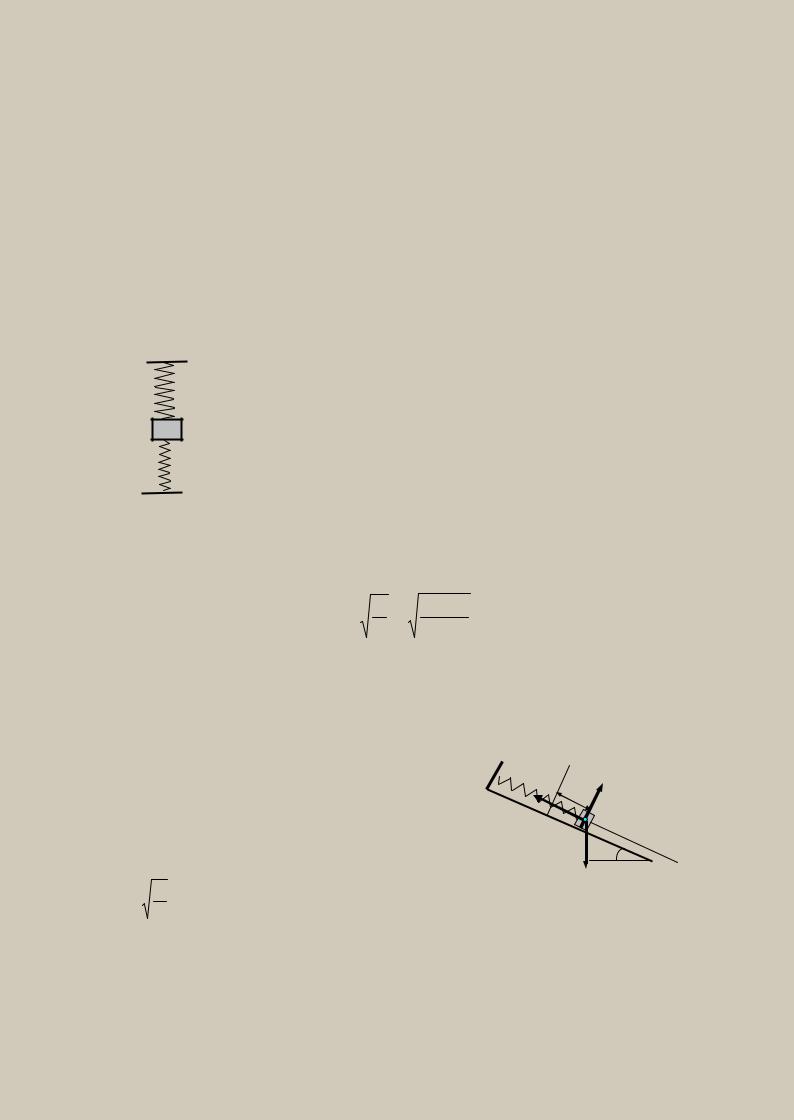
Пример 4. На конец пружины, закрепленной на гладкой наклонной плоскости, без начальной скорости прикрепляют груз массой m. Коэффициент жесткости пружины равен с, угол наклона – β. Определить колебания груза на пружине (рис.7).

Груз совершает гармонические

	колебания, уравнение которых имеет вид:	F λст	N
	x = a sin(kt +α) ,	А	О	х
			β
	где а – амплитуда, α – начальная фаза,	mg
	k = mс – частота колебаний.	Рис. 7

Груз подвешивают к концу недеформированной пружины, а начало отсчета координаты х выбирается в

положении статического равновесия, следовательно, начальная координата равна статическому удлинению пружины, взятому со знаком минус: х0 = −λст . Начальная скорость х& = 0 .

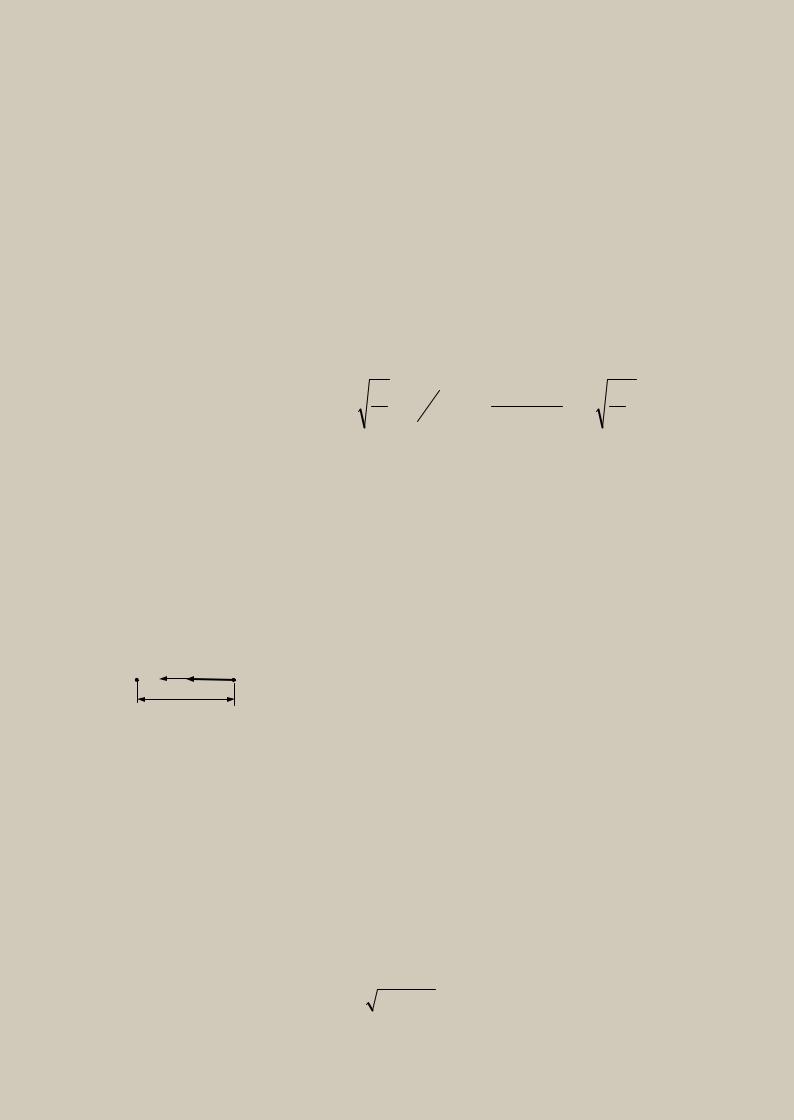
Определимзначение λст, составив уравнения равновесия груз на наклонной плоскости:

∑Fkx = mg sin β −F ст =0 .

Подставим в это уравнение значение силы упругости в положении ста-

тического равновесия Fст = cλcn ,		получим					mg sin β
mg sin β −cλст = 0 , отсюда					λст =				.
							c
Следовательно, начальная координата					х0 = −	mg sin β		.
							c
Для определения амплитуды и начальной фазы подставим в выражения
(3.6) начальные условия, получим		а = λст,			tgα = ∞, α = π/2.
Окончательно, уравнение движения груза запишется в виде:
x = −λcn sin(	c t +π		2	) = − mg sin β cos						c t.
	m					c				m

		2. Колебания материальной точки				при наличии			сил
		сопротивления
		Пусть		на материальную точку	действуют	восстанавливающая			сила
	F	= −c OM		и сила сопротивления,	пропорциональная скорости,
							R	= −βV

(рис.8). Определим движение точки для случая, когда в начальный момент

при t = 0

x0

= 0,

x0 =V0 .

&

О F

R

М

х

Составим

дифференциальное

уравнение дви-

жения точки под действием указанных сил:

х

Рис.3.8

m

d 2 x

&

= −cx − β x .

dt 2

на m

Преобразуем

это

уравнение,

разделив

и обозначив

2n =

β

k

2

c

,

=

:

m

m

&&

&

2

x = 0,

(10)

x

+2nx +k

Уравнение (10) – однородное линейное дифференциальное уравнение второго порядка, характеристическое уравнение которого имеет вид

r 2 +2nr +k 2 = 0 . Корни характеристического уравнения равны

r1,2 = −n ± n2 −k 2 .

(11)

Характер движения существенно зависит от соотношения между величинами n и k. Различаются три вида движения:

а) n< k – случай малого сопротивления; б) n = k – предельный случай;

в) n> k – случай большого сопротивления/

2.1. Затухающие колебания

Рассмотрим движение материальной точки при малом сопротивлении, для которого n< k.

В этом случае корни характеристического уравнения (11) будут комплексными, т.е.

r1,2 = −n ±i k 2 −n2 .

Следовательно, уравнение движения точки имеет вид

x = e−nt (C1 cos

k 2 −n2 t +C2 sin

k 2 −n2 t).

(12)

Для определения постоянных интегрирования С1, С2

вычислим

&

−nt

(−C1

k

2

−n

2

sin k

2

−n

2

t +C2

k

2

−n

2

cos k

2

−n

2

t)

−

x = e

−ne−nt (C cos

k 2 −n2 t +C

sin

k 2 −n2 t).

(13)

2

1

Подставим в (12) и (13) начальные условия: t = 0, x0 = 0, x0 =V0 .

&

Получим

0 = C1 , V0 = C2 k 2 −n2 −nC1 ,

откуда

С1 = 0 ,

C2

=

V0

.

k 2

− n2

Тогда уравнение движения точки (12) запишется в виде

x = e

−nt

V0

sin

k

2

−n

2

t .

(14)

k 2

−n2

Обозначим

А=

V0

,

k1 =

k 2 −n2

Тогда

k 2 −n2

x = Ae−nt sin k1t .

(15)

Движение груза, описываемое уравнением (15), представляет собой затухающие колебания, так как при t→ ∞ x→ 0 (рис.9).

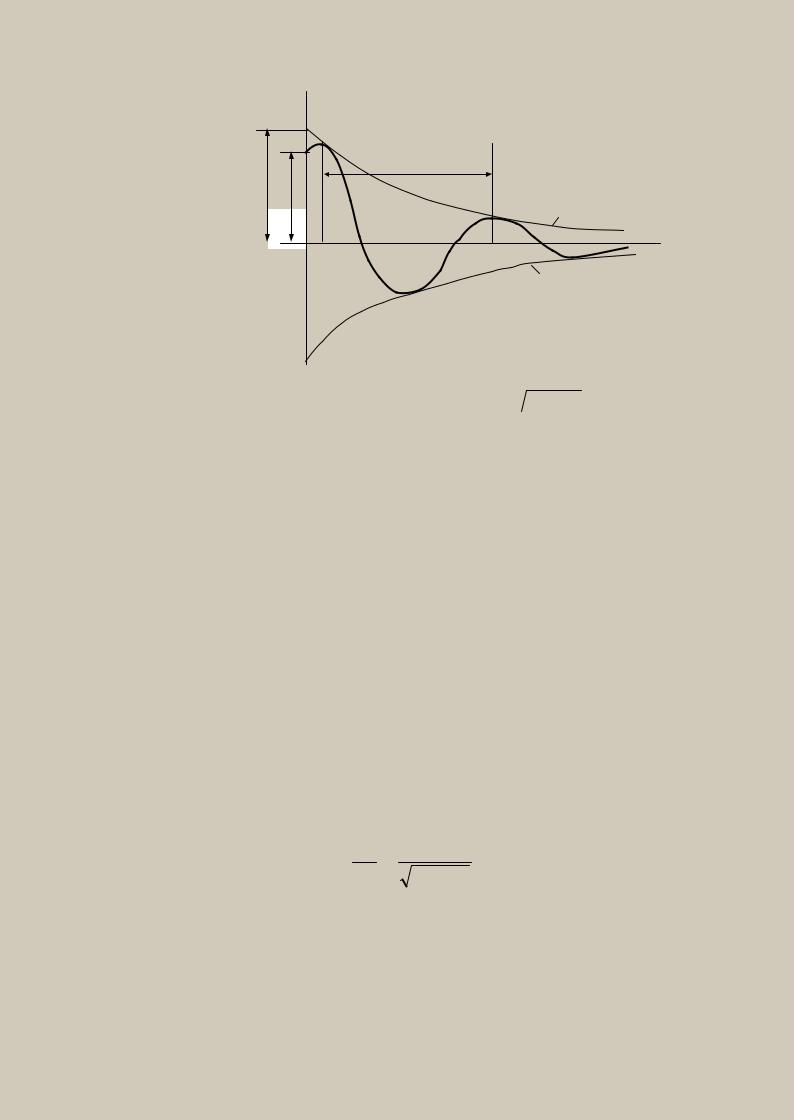
a х0

х

T

x = ae-nt

t

О t

t+T

x = - ae-nt

Рис.9

Частота затухающих колебаний равна k1 =k 2−n2 .

Периодом затухающих колебаний ТС называется промежуток времени между двумя последовательными максимальными отклонениями точки в одном направлении.

Рассмотрим два последовательных максимальных отклонения в одном направлении в моменты времени t и t+TС .

В моменты максимальных отклонений скорость точки равна нулю, поэтому в момент времени t

	Vx1	= −nAe−nt cos k1t +k1 Ae−nt sin k1t = 0 , откуда	tg k1t =	k1	.
	В момент времени t +TC			n
						k1
	Vx2 = −nAe−nt cos(k1t +TC ) +k1 Ae−nt sin(k1t +TC ) = 0 , откуда			tg k1t =
						n
		tg k1t = tg (k1t +TС ) .
	Следовательно,

Равные значения тангенсов повторятся при минимальной разности значений

их аргументов, равной 2π:		k1t +TС −k1t = 2π .
Значит,	TС	= 2π =	2π	.
		k1	k 2 − n2
Из этой формулы следует, что при наличии силы сопротивления период
затухающих	колебаний	больше	периода незатухающих колебаний:

TC f T .

Амплитудой затухающих колебаний называют наибольшее отклоне-

ние точки от положения равновесия: