
- •10. Уравнение прямой, заданной точкой и направляющим вектором.
- •11. Уравнение прямой, с угловым коэффициентом.
- •13. Взаимное расположение двух прямых.
- •17. Уравнение плоскости заданной точкой и двумя параллельными ей векторами.
- •18. Уравнение плоскости заданной тремя точками.
- •19. Уравнение плоскости, заданной точкой Мо и вектором нормали. Определение. Вектор, перпендикулярный плоскости, называется вектором нормали плоскости.
- •20. Взаимное расположение двух плоскостей.
- •23. Уравнение прямой, заданной как линия пересечения двух плоскостей.
- •25. Исследование формы эллипса по его уравнению
- •26. . Исследование формы гиперболы по её уравнению
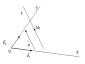
9. Деление отрезка в данном отношении.
Пусть дана прямая ℓ и точки А, В и С принадлежащие прямой ℓ.
Определение.
Отношением,
в котором точка С делит отрезок АВ
называется число
 . Обозначение λС=(АВ,С).
. Обозначение λС=(АВ,С).
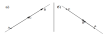 Число
λ может принимать как положительные
так и отрицательные значения. Так, на
рис. а) векторы
Число
λ может принимать как положительные
так и отрицательные значения. Так, на
рис. а) векторы
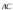 и
и
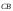 сонаправлены
и,
поэтому, λ > 0; то есть точка С лежит
на отрезке АВ. В случае, приведённом на
рис.4б),
сонаправлены
и,
поэтому, λ > 0; то есть точка С лежит
на отрезке АВ. В случае, приведённом на
рис.4б),
 и
и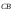 противоположно направлены и, следовательно,
λ < 0, а точка С лежит вне отрезка АВ.
Число
λ не может принимать значение равное
− 1, так как в этом случае
противоположно направлены и, следовательно,
λ < 0, а точка С лежит вне отрезка АВ.
Число
λ не может принимать значение равное
− 1, так как в этом случае
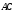 = −
= −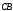 =>
=>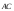 =
=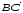 => А = В, что означает отрезов вырождается
в точку.
=> А = В, что означает отрезов вырождается
в точку.
10. Уравнение прямой, заданной точкой и направляющим вектором.
Поставим
перед собой задачу получить уравнение
прямой. Введём на плоскости аффинную
систему координат R=(О,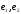 )
и рассмотрим прямую ℓ, заданную точкой
Мо(хо,уо)
и вектором
)
и рассмотрим прямую ℓ, заданную точкой
Мо(хо,уо)
и вектором
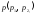 параллельным ей.
параллельным ей.

В этом случае положение прямой ℓ на плоскости определяется единственным образом.
Пусть
точка М(x;y)
− произвольная точка прямой ℓ. Очевидно,
что точка М(x,y)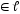 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы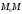 и
и параллельны. =>
параллельны. => .
Координаты вектора
.
Координаты вектора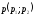 и вектора
и вектора
 (
(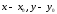 )
известны, =>
)
известны, =>
Уравнение называется уравнением прямой заданной точкой и направляющим вектором или каноническим уравнением прямой.
(Уравнение прямой, проходящей через две точки.
Согласно аксиомам планиметрии через две точки плоскости проходит единственная прямая.
Пусть
на плоскости введена аффинная система
R=(О, )
координат и даны две точки, которые
имеют координаты М1(х1;у1)
и М2
(х2;у2).
)
координат и даны две точки, которые
имеют координаты М1(х1;у1)
и М2
(х2;у2).

В
этом случае в качестве направляющего
вектора прямой можно взять вектор
 .
.
образом
направляющий вектор прямой ℓ
 =
=
=
=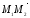 =(
=( ).
Уравнение прямой (М1М2)
в этом случае запишется в виде:
).
Уравнение прямой (М1М2)
в этом случае запишется в виде:
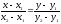
Уравнение называется уравнением прямой проходящей через две точки).
11. Уравнение прямой, с угловым коэффициентом.
Пусть
на плоскости в дана аффинная система
координат R=(О, )
и дана прямая ℓ, пересекающая ось
ординат.
)
и дана прямая ℓ, пересекающая ось
ординат.
Если
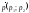 − направляющий вектор прямой, то
− направляющий вектор прямой, то и
и не коллинеарны, поэтому
не коллинеарны, поэтому .
.
 Число
Число
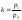 называетсяугловым
коэффициентом прямой ℓ.
Заметим, что угловой коэффициент прямой
не зависит от выбора направляющего
вектора прямой. Действительно, если
называетсяугловым
коэффициентом прямой ℓ.
Заметим, что угловой коэффициент прямой
не зависит от выбора направляющего
вектора прямой. Действительно, если
 − другой направляющий вектор прямой
ℓ, то
− другой направляющий вектор прямой
ℓ, то поэтому координаты векторов
поэтому координаты векторов
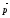 и
и
 пропорциональны
пропорциональны
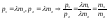 .Пустьk
− коэффициент прямой ℓ, координат
R=(О,
.Пустьk
− коэффициент прямой ℓ, координат
R=(О,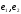 ).
Очевидно, что если
).
Очевидно, что если направляющий вектор прямой ℓ, то вектор
направляющий вектор прямой ℓ, то вектор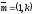 является направляющим вектором этой
прямой. Поэтому уравнение (5) можно
записать в виде
является направляющим вектором этой
прямой. Поэтому уравнение (5) можно
записать в виде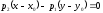 или
или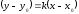 .
.
в качестве точки М(х0;у0) взять точку В(0;b), то последнее уравнение примет вид
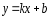
Это уравнение называется уравнением прямой с угловым коэффициентом.
Угловой
коэффициент k
прямой имеет простой геометрический
смысл, если прямая задана в прямоугольной
системе координат R(O,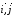 ),
что угловой коэффициент прямой равен
тангенсу угла наклона прямой к оси Ох.
),
что угловой коэффициент прямой равен
тангенсу угла наклона прямой к оси Ох.
12. Прямая, как линия первого порядка. Определение. Линия называется линией первого порядка, если её уравнение содержит переменные в первой степени.
Теорема I. Любая прямая в некоторой системе координат на плоскости определяется уравнением первого порядка Ах+Ву+C =0.
И наоборот любое уравнение первого порядка Ах+Ву+C =0 в некоторой системе координат на плоскости задаёт в пряммую.
Доказательство.
1.
Пусть на плоскости дана прямая ℓ. Введём
на плоскости систему координат. Тогда,
в зависимости от способа задания прямой
её уравнением будет одно из следующих:
 ;
;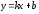 ;
;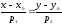
 ;
;

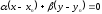 .Каждое
из этих уравнений является уравнением
первого порядка, которое легко приводится
к видуLx+By+C=0
.Ч.т.д.
.Каждое
из этих уравнений является уравнением
первого порядка, которое легко приводится
к видуLx+By+C=0
.Ч.т.д.
2. Пусть на плоскости в некоторой системе координат дано уравнение Lx+By+C=0. Выясним, какая фигура Φ определяется этим уравнением.
Возьмём
точку М0(-С/L;
0) и вектор
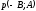 .
.
Составим
уравнение прямой ℓ, заданной точкой М0
и направляющим вектором
 .
.
Раскрыв определитель, получим Ах+Ву+Сz=0.
Очевидно,
что всякая точка, принадлежащая фигуре
Φ имеет координаты, удовлетворяющие
уравнению Ах+Ву+Сz=0.
С
другой стороны, Любая точка, принадлежащая
прямой ℓ
 ,
имеет координаты, удовлетворяющие тому
же уравнению, => фигура Φ является
прямой ℓ .
,
имеет координаты, удовлетворяющие тому
же уравнению, => фигура Φ является
прямой ℓ .
Теорема доказана.
