
- •10. Уравнение прямой, заданной точкой и направляющим вектором.
- •11. Уравнение прямой, с угловым коэффициентом.
- •13. Взаимное расположение двух прямых.
- •17. Уравнение плоскости заданной точкой и двумя параллельными ей векторами.
- •18. Уравнение плоскости заданной тремя точками.
- •19. Уравнение плоскости, заданной точкой Мо и вектором нормали. Определение. Вектор, перпендикулярный плоскости, называется вектором нормали плоскости.
- •20. Взаимное расположение двух плоскостей.
- •23. Уравнение прямой, заданной как линия пересечения двух плоскостей.
- •25. Исследование формы эллипса по его уравнению
- •26. . Исследование формы гиперболы по её уравнению
17. Уравнение плоскости заданной точкой и двумя параллельными ей векторами.
Пусть дана
точка М0(x0,y0,z0)
и два параллельных ей вектора
 и
и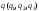 составим уравнение этой плоскости δ.
Для определения координат вектора
нормали
составим уравнение этой плоскости δ.
Для определения координат вектора
нормали
 этой плоскости
поступим следующим образом.
этой плоскости
поступим следующим образом.
а) Запишем
уравнение плоскости δ, проходящей через
точку М1
перпендикулярно некоторому вектору
 :
δ:
:
δ: б)
Так как векторы
б)
Так как векторы
 и
и параллельны
плоскости δ, то воспользуемся условиям
(7) параллельности этих векторов плоскости
δ.
параллельны
плоскости δ, то воспользуемся условиям
(7) параллельности этих векторов плоскости
δ.
 в)
В результате получаем, что координаты
вектора нормали плоскости δ должны
являться решением системы уравнений:
в)
В результате получаем, что координаты
вектора нормали плоскости δ должны
являться решением системы уравнений:
 (10)
(10)
Система уравнений
(10)является системой линейных одноородных
уравнений относительно неизвестных
координат вектора нормали плоскости
δ. Она имеет ненулевое решение, если
определитель системы равен нулю. Таким
образом, для плоскости, проходящей через
точку М0
параллелно векторам
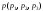 и
и
 должно выполняться условие
должно выполняться условие
 .
(11)
.
(11)
Соотношение (11) является уравнением относительно неизвестных x, y и z, которые являются координатами любой точки М(x;у;z) плоскости σ, его называют уравнением плоскости, проходящей через точку параллельно двум векторам.
18. Уравнение плоскости заданной тремя точками.
Согласно аксиомам геометрии через любые три точки пространства проходит единственная плоскость. Получим уравнение плоскости проходящей через три точки М1(x1;y1;z1), М2(x2;y2;z2), М3(x3;y3;z3).

Для решения этой
задачи воспользуемся уравнением
 ,
считая , что
,
считая , что ,
и
,
и .
В этом случае уравнение плоскости σ,
проходящей через точки М1(x1;y1;z1),
М2(x2;y2;z2),
М3(x3;y3;z3),
запишется в виде
:
.
В этом случае уравнение плоскости σ,
проходящей через точки М1(x1;y1;z1),
М2(x2;y2;z2),
М3(x3;y3;z3),
запишется в виде
:
 (12)
(12)
Соотношение (12) это уравнение относительно неизвестных x, y и z, которые являются координатами любой точки М(x;у;z) плоскости σ, его называют уравнением плоскости, проходящей через три точки .
19. Уравнение плоскости, заданной точкой Мо и вектором нормали. Определение. Вектор, перпендикулярный плоскости, называется вектором нормали плоскости.
Поставим перед собой задачу получить уравнение плоскости в пространстве, заданной точкой и вектором нормали.
Введём пространстве
прямоугольную систему координат и
рассмотрим плоскость, заданную точкой
Мо(хо,уо)
и вектором
 перпендикулярным плоскости α. Приведённые
данные определяют положение плоскости
α в пространстве единственным образом.
перпендикулярным плоскости α. Приведённые
данные определяют положение плоскости
α в пространстве единственным образом.
Пусть
точка М(x;y;z)
− произвольная точка плоскости α.
Очевидно, что точка М(x,y,z) тогда и только тогда, когда векторы
тогда и только тогда, когда векторы и
и взаимно
перпендикулярны. =>
взаимно
перпендикулярны. =>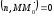 .
Координаты вектора
.
Координаты вектора и вектора
и вектора (
( )
известны, =>
)
известны, =>

Уравнение называется уравнением плоскости,
заданной точкой Мо(хо,уо)
и вектором нормали
называется уравнением плоскости,
заданной точкой Мо(хо,уо)
и вектором нормали
 .
.
20. Взаимное расположение двух плоскостей.
Теорема IV. Пусть в некоторой аффинной системе координат даны плоскости α: А1 х+В1 у+С1 z+D1 =0 и β: А2 х+В2 у+С2 z+D2 =0. Тогда:
1) α = β <= >
А1,
В1,
С1,
D1
и
А2
, В2
, С2
, D2
- пропорциональны, то есть:
 ,
,
2) α ‖ β <= >
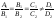
3) α ∩ β ≠ Ø <= > А1, В1, С1, D1 и А2 , В2 , С2 , D2 - не пропорциональны.
Доказательство.
Необходимость.
Пусть для плоскостей
α
и β
выполнено условие
 =λ
илиА1
= λ
А2
;
В1
=
λ В2
;
С1=
λС2
; D1=
λD2
.
Это
означает, что уравнение плоскости
α
можно записать в виде: λ(А2
х+В2+
у+С2
z+D2)
=0
<=> любая точка плоскости β
принадлежит плоскости α
то есть эти плоскости совпадают.
=λ
илиА1
= λ
А2
;
В1
=
λ В2
;
С1=
λС2
; D1=
λD2
.
Это
означает, что уравнение плоскости
α
можно записать в виде: λ(А2
х+В2+
у+С2
z+D2)
=0
<=> любая точка плоскости β
принадлежит плоскости α
то есть эти плоскости совпадают.
Достаточность.
Пусть α = β = > векторы нормали плоскостей α и β коллинеарны, то есть А1 = λ А2 ; В1 = λ В2 ; С1= λС2 . Это означает, что уравнение плоскости α можно записать в виде: λ(А2 х+В2 у+С2 z)+D1 =0. = > D1 = - λ(А2 х+В2 у+С2 z) = λD2 = > А1 = λ А2 ; В1 = λ В2 ; С1= λС2 ; D1= λD2 .
2) Необходимость.
Пусть для плоскостей
α
и β
выполнено условие
 .
В этом случае векторы нормали плоскостейα
и β
коллинеарны, а значит плоскости α
и β
параллельны, но не совпадают, так как
для совпадения плоскостей α
и β необходимо
и достаточно, что бы
.
В этом случае векторы нормали плоскостейα
и β
коллинеарны, а значит плоскости α
и β
параллельны, но не совпадают, так как
для совпадения плоскостей α
и β необходимо
и достаточно, что бы
 .
.
Достаточность.
Пусть α
‖ β . =
> что
векторы нормали
 и
и
 коллинеарны, а это значит, что А1
= λ А2 ;
В1
= λ
В2
;
С1=
λС2,
но D1≠
λD2
так
α ≠ β.
коллинеарны, а это значит, что А1
= λ А2 ;
В1
= λ
В2
;
С1=
λС2,
но D1≠
λD2
так
α ≠ β.
3) Необходимость.
Пусть α
∩ β ≠ Ø.
= > что
векторы нормали

 не коллинеарны, а это значит, что
А1,
В1,
С1
и А2
, В2
, С2
- не пропорциональны.
не коллинеарны, а это значит, что
А1,
В1,
С1
и А2
, В2
, С2
- не пропорциональны.
Достаточность.
Пусть
А1,
В1,
С
и А2
, В2
, С2
- не
пропорциональны.
= >
что векторы нормали

 не
коллинеарны,
а это значит, что >
А1,
В1,
С1,
1
и А2
, В2
, С2
, - не пропорциональны.
не
коллинеарны,
а это значит, что >
А1,
В1,
С1,
1
и А2
, В2
, С2
, - не пропорциональны.
21. Геометрический смысл знака многочлена Ах+Ву+Сz+D.
Теорема III.
Если в
аффинной системе координат дана плоскость
α: Ах+Ву+Сz+D=0,
и точка М1(x1;y1;z1),координаты
которой удовлетворяют неравенству Ах1+
Ву1+
Сz1+D
> 0, то точка М1
лежит
по одну сторону от плоскости α с концом
вектора
 ,
если его начало приложить к некоторой
точке плоскости. Если координаты и точки
М1(x1;y1;z1)
удовлетворяют неравенству Ах1+
Ву1+
Сz1+D<
0, то точка М1
с концом вектора
,
если его начало приложить к некоторой
точке плоскости. Если координаты и точки
М1(x1;y1;z1)
удовлетворяют неравенству Ах1+
Ву1+
Сz1+D<
0, то точка М1
с концом вектора
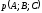 лежит
по разные стороны от плоскости α, если
начало вектора приложить к некоторой
точке плоскости.
лежит
по разные стороны от плоскости α, если
начало вектора приложить к некоторой
точке плоскости.
Доказательство.
Прежде, чем привести
доказательство сформулированной
теоремы, заметим, что вектор
 не параллелен плоскостиα.
Для того чтобы убедиться в этом проверим
условие параллельности вектора
не параллелен плоскостиα.
Для того чтобы убедиться в этом проверим
условие параллельности вектора
 плоскости
α : А2 +
В2
+ С2
≠ 0.
плоскости
α : А2 +
В2
+ С2
≠ 0.
Пусть в пространстве
введена аффинная система координат
R=(О )
и дан многочленАх+
Ву+ Сz+D.
Если в этот многочлен подставит координаты
точки М1,
то значением этого многочлена буде
некоторое число δ. Возможны следующие
случаи:
)
и дан многочленАх+
Ву+ Сz+D.
Если в этот многочлен подставит координаты
точки М1,
то значением этого многочлена буде
некоторое число δ. Возможны следующие
случаи:
 .
.
В случае б) точка М1 принадлежит плоскости α. Выясним, где находится точка М1 в двух остальных случаях.
Проведём
через точку М1
прямую М1Н
параллельно вектору
 ,
Тогда так как
,
Тогда так как
 ‖
‖ ,
то
,
то =λ·
=λ· => хН -
х1 =
λА; уН -
у1 =
λВ; zН
- z1
= = λС. =>
х1 =
λА + хН ;
у1 =
λВ + уН
; z1
= λС + zН
(13)
=> хН -
х1 =
λА; уН -
у1 =
λВ; zН
- z1
= = λС. =>
х1 =
λА + хН ;
у1 =
λВ + уН
; z1
= λС + zН
(13)
Подставив выражения для x1; y1 и z1 в многочлен Ax + By + Cz + D , получаем: δ = Ax1 + By1 + Cz 1+ D = λ(А2 + В2 +C2) + AxH + ByH + CzH + D .
Так как точка Н
принадлежит плоскости α, то сумма
подчёркнутых слагаемых равна 0. Таким
образом δ = λ(А2
+ В2
+C2).
Отсюда получаем, что знак δ зависит от
знака
 λ.=> Если λ >
0 , то вектор
λ.=> Если λ >
0 , то вектор
 и вектор
и вектор
 сонаправлены и их концы расположены по
одну сторону от плоскости α. Если λ <
0 , то вектор
сонаправлены и их концы расположены по
одну сторону от плоскости α. Если λ <
0 , то вектор и вектор
и вектор
 противоположно направлены и их концы
расположены по разные стороны от
плоскости α. (Рис.11).
противоположно направлены и их концы
расположены по разные стороны от
плоскости α. (Рис.11).

Теорема доказана.
16. Геометрический смысл знака трёхчлена Ах+Ву+С.
Теорема
III.
Если
в аффинной системе координат дана
прямаяℓ: Ах+Ву+С=0, и точка М1(x1;y1),координаты
которой удовлетворяют неравенству Ах1+
Ву1+
С > 0, то точка М1
лежит
по одну сторону от прямой ℓ с концом
вектора
 ,
если его начало приложить к некоторой
точке прямойℓ. Если координаты и точки
М1(x1;y1)
удовлетворяют неравенству Ах1+
Ву1+
С< 0, то точка М1
с концом вектора
,
если его начало приложить к некоторой
точке прямойℓ. Если координаты и точки
М1(x1;y1)
удовлетворяют неравенству Ах1+
Ву1+
С< 0, то точка М1
с концом вектора лежат
по разные стороны от прямойℓ, если
начало вектора приложить к некоторой
точке прямой ℓ.
лежат
по разные стороны от прямойℓ, если
начало вектора приложить к некоторой
точке прямой ℓ.
Доказательство.
Прежде,
чем привести доказательство сформулированной
теоремы, заметим, что вектор
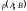 не параллелен плоскостиα.
Для того чтобы убедиться в этом проверим
условие параллельности вектора
не параллелен плоскостиα.
Для того чтобы убедиться в этом проверим
условие параллельности вектора
 плоскости
α : А2
+
В2
+ С2
≠
0.
плоскости
α : А2
+
В2
+ С2
≠
0.
Пусть
в пространстве введена аффинная система
координат R=(О )
и дан многочленАх+
Ву+ Сz+D.
Если в этот многочлен подставит координаты
точки М1,
то значением этого многочлена буде
некоторое число
)
и дан многочленАх+
Ву+ Сz+D.
Если в этот многочлен подставит координаты
точки М1,
то значением этого многочлена буде
некоторое число
δ.
Возможны следующие случаи:
 .
.
В случае б) точка М1 принадлежит плоскости α. Выясним, где находится точка М1 в двух остальных случаях.

Проведём
через точку М1
прямую М1Н
параллельно вектору
 ,
Тогда так как
,
Тогда так как
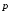

 ,
то
,
то
 =λ·
=λ· => хН
-
х1
=
λА; уН
-
у1
=
λВ; . => х1
=
λА + хН
;
у1
=
λВ + уН
(10)
=> хН
-
х1
=
λА; уН
-
у1
=
λВ; . => х1
=
λА + хН
;
у1
=
λВ + уН
(10)
Подставив выражения для x1; y1 и z1 в многочлен Ax + By + C , получаем: δ = Ax1 + By1 + C = λ(А2 + В2 ) + AxH + ByH + C.
Так
как точка Н принадлежит прямой ℓ, то
сумма подчёркнутых слагаемых равна 0.
Таким образом δ = λ(А2
+ В2
). Отсюда получаем, что знак δ зависит
от знака
 λ.=>
Если λ > 0 , то вектор
λ.=>
Если λ > 0 , то вектор
 и
вектор
и
вектор
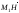 сонаправлены и их концы расположены по
одну сторону отпрямой
ℓ.
Если λ < 0 , то вектор
сонаправлены и их концы расположены по
одну сторону отпрямой
ℓ.
Если λ < 0 , то вектор
 и
вектор
и
вектор
 противоположно направлены и их концы
расположены по разные стороны отпрямой
ℓ.
противоположно направлены и их концы
расположены по разные стороны отпрямой
ℓ.
Теорема доказана.
22. Уравнения прямой, заданной точкой и направляющим вектором. Определение. Направляющим вектором прямой называется любой вектор параллельный этой прямой.
А) Прямая имеет
бесконечное множество направляющих
векторов, которые коллинеарны между
собой. Пусть
в пространстве дана точка М0
и вектор
 .
Через точку М0
в пространстве так же как и на плоскости
можно провести единственную прямую.
Составим уравнение этой прямой.
.
Через точку М0
в пространстве так же как и на плоскости
можно провести единственную прямую.
Составим уравнение этой прямой.
Дано:
R=(О, ).
).
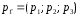 ǀǀ ℓ
М0(x0;y0;z0)
ǀǀ ℓ
М0(x0;y0;z0) ℓCоставить
уравнение ℓ.
ℓCоставить
уравнение ℓ.
Решение.

Возьмём произвольную точку М(x;y;z), принадлежащую прямой ℓ.
Очевидно, что
М0(x0;y0;z0) ℓ
<=>
ℓ
<=> .
Если векторы коллинеарны, то координаты
этих векторов пропорциональны . Таким
образом:
.
Если векторы коллинеарны, то координаты
этих векторов пропорциональны . Таким
образом:

─ уравнения прямой, заданной точкой и направляющим вектором. В записи этих уравнений содержится два знака равенства, поэтому это не одно уравнение, а краткая запись системы двух уравнений :

В этих уравнениях
x0,
y0,z0
─ координаты данной точки М0,
принадлежащей прямой, р1,
р2,
р3
─ координаты направляющего вектора
прямой, а x,
y
и z
─ координаты текущей (любой точки)
прямой. Уравнения
 называютканоническими
уравнениями прямой ℓ.
называютканоническими
уравнениями прямой ℓ.
б) Параметрические
уравнения прямой.
Пусть в аффинной системе координат
прямая ℓ задана точкой М0(x0;y0;z0)
и направляющим вектором
 .
В этом случае векторы
.
В этом случае векторы и
и коллинеарны. Отсюда следует что существует
такое число t, что
коллинеарны. Отсюда следует что существует
такое число t, что . Таким образом
. Таким образом =>
=> (17)
(17)
Эти равенства (17) называются параметрическими уравнениями прямой. Здесь t ─ параметр. Его смысл заключается в том, что для любого действительно числа t точка с координатами (х,у,z), удовлетворяющая условиям (17) лежит на прямой ℓ. Обратно, если (х,у,z) – точка прямой ℓ, то всегда найдется такое число t, что х, у и z выражаются через х0, у0 и z0, р1, р2 и р3 при помощи равенств (17).
