Лекції з вищої математики

20

множенням елементiв другого рядка матрицi A на вiдповiднi координати вектора ~x i тодi додаємо отриманi добутки:

2	1 5 3	32 x2	3	= 2	x1 + 5x2	3x3	3:
4		x1	5	4			5
	54 x3

Таким же чином, третiй елемент у A~x може бути обчислений множенням елементiв третього рядка матрицi A на вiдповiднi координати вектора ~x.

Рядково-векторне правило для обчислення A~x

Якщо добуток A~x визначений, то i-ий елемент у A~x рiвний сумi добуткiв вiдповiдних елементiв з i-го рядка матрицi A i координат вектора ~x.

ПРИКЛАД 7.

		0 5			3	2	4	3				0 4 + ( 5) 3 + 3 7											6
а).							7
		1		2	1	4	3	5	=			1 4 + 2 3 + ( 1)						7			=		3 :
б).	2		2	3	3					2		4 +	( 3) 7		3		= 2		13		3
			8	0		7	= 2					8 4 + 0 7							32
						4
	4	1	5	2				4		( 5) 4 + 2 7					5r		4			6	5
			0	0	5	r				1 r + 0 s + 0										r
	2				32 s		3		2								3 =				3
в).		0	1	0				=		0		r + 1		s + 0		r		2 s				:
	4	0	0	1	54	t	5 4			0		r + 0		s + 1		r	5 4			t	5

Матриця у прикладi 7 в), з одиницями на дiагоналi i нулями у всiх iнших мiсцях, називається одиничною матрицею i позначається через I (у багатьох посiбниках позначають через E). Обчислення у частинi в) показують, що I~x = ~x для кожного ~x з R3. Iснує аналогiчна n n одинична матриця, яку iнодi позначають через In. Легко показати, що I~x = ~x для кожного ~x з Rn.

Властивостi матрично-векторного добутку A~x

Факти у наступнiй теоремi важливi i будуть використовуватися впродовж вивчення курсу. Доведення грунтуються на означеннi A~x i алгебраїчних властивостях Rn.

ТЕОРЕМА 5.

Якщо A є m n матриця, ~u i ~v вектори з Rn i c скаляр, то:		a) A(~u + ~v) = A~u + A~v;
		б)	A(c~u) = c(A~u):
ДОВЕДЕННЯ. Для спрощення вiзьмемо n = 3; A =		~a1	~a2 ~a3	i ~u, ~v вектори з
R3 (доведення загального випадку подiбне). Для i =	1; 2; 3 нехай ui			i vi будуть i-тi

координати векторiв ~u i ~v вiдповiдно. Для доведення твердження обчислимо A(~u + ~v) як лiнiйну комбiнацiю стовпцiв, використовуючи координати ~u + ~v як ваги.

2 3

u1 + v1

A(~u + ~v) = ~a1 ~a2 ~a3 4 u2 + v2 5 u3 + v3

=(u1 + v1)~a1 + (u2 + v2)~a2 + (u3 + v3)~a3

=(u1~a1 + u2~a2 + u3~a3) + (v1~a1 + v2~a2 + v3~a3)

=A~u + A~v:

				21
A(c~u) = ~a1 ~a2 ~a3		2 cu2	3 = (cu1)~a1 + (cu2)~a2 + (cu3)~a3
		cu1
		cu3
= c(u1~a1) + c(u2~a24) + c(u53~a3)

= c(u1~a1 + u2~a2 + u3~a3) = c(A~u):

4. Властивостi множин розв’язкiв систем лiнiйних рiвнянь.

Множини розв’язкiв лiнiйних систем є важливими об’єктами для вивчення у лiнiйнiй алгебрi. Ми розглянемо властивостi таких множин та використаємо поняття вектора для того, щоб дати явнi геометричнi описи цих множин розв’язкiв.

Однорiднi лiнiйнi системи

Система лiнiйних рiвнянь називається однорiдною, якщо вона може бути записана

	~	~	m
	у виглядi A~x = 0, де A є m n матриця i 0 є нульовий вектор у R			. Така система
	~	~			n
	A~x = 0 завжди має принаймнi один розв’язок, а саме, 0 (нульовий вектор у R					). Цей
	нульовий розв’язок називають			~
		тривiальним. Для даного рiвняння A~x = 0 важливим

питанням є чи iснує нетривiальний розв’язок, тобто, чи є ненульовий вектор ~x такий,

що задовольняє рiвняння ~ ~. Теорема iснування i єдиностi, розглянута нами ранiше,

Ax = 0

негайно приводить до наступного факту.

Однорiдне рiвняння ~ ~ має нетривiальний розв’язок тодi i тiльки тодi, коли

Ax = 0

рiвняння має хоча б одну вiльну змiнну.

ПРИКЛАД 8. Встановити чи має нетривiальний розв’язок наступна однорiдна система. Тодi описати множину розв’язкiв.

8	3x1	+	2x2	+	4x3	=	0;
<	3x1		5x2		4x3	=	0;

:6x1 + x2 8x3 = 0:

Роз’вязання. Нехай A є матрицею коефiцiєнтiв системи i рядкова редукцiя розширеної

матрицi j~ до ступiнчатої форми:

[A 0]

2	3		2	4		0 3 2				0	3	0	0		3 2 0 3			0		0 3	:
	3		5	4		0				3	5	4		0		3	5	4		0
4 6		1 8				0 5 4 0 9						0	0 5 4 0 0					0		0 5
										~	має нетривiальний розв’язок (один для кожного
З вiльною змiнною x3, рiвняння A~x = 0
																					~
вибору x3). Щоб описати множину розв’язкiв, продовжимо рядкову редукцiю [A j0] до
зведеної ступiнчастої форми:
		2	1	0	34 0				3;		x1					34 x3 = 0;
			0	1	0 0						8	x2					= 0;
		4	0	0	0 0				5		<					0 = 0:
Розв’язуємо для базисних змiнних x1; x2:i отримуємо x1 = 34 x3, x2 = 0; з вiльною x3. Як
вектор, загальний розв’язок								~
					A~x = 0 має форму:
~x =		2 x2		3 = 2			4	0	3		4	3 = x3~v; де ~v =						2	4
							3			= x3 2 0									0 3:
			x1	5 4				x3	5		3								3
		4 x3						x3			4 1 5							4 1 5

Тут x3 є множником виразу для загального векторного розв’язку. Це показує, що кожний

~	у цьому випадку є добуток скаляра на ~v. Тривiальний розв’язок одер-
розв’язок A~x = 0

жимо вибираючи x3 = 0. Геометрично, множина розв’язкiв є пряма, яка проходить через

~ у 3. Дивись рисунок 6.

0 R

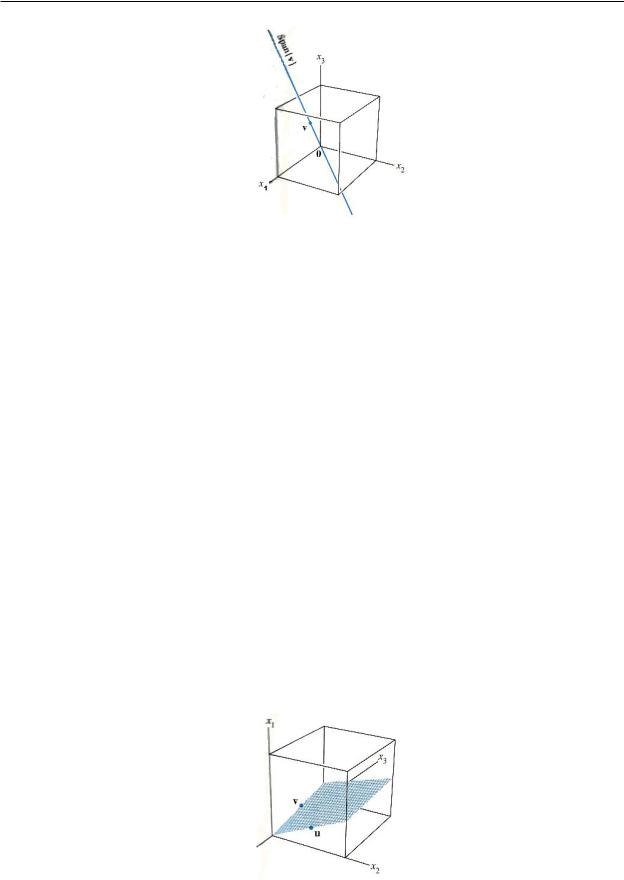
22

Рисунок 6.

Зауважимо, що нетривiальний розв’язок A~x може мати нульовi координати, але принаймнi одна координата повинна бути вiдмiнною вiд нуля.

ПРИКЛАД 9. Єдине лiнiйне рiвняння може бути розглянуто як дуже проста система рiвнянь. Описати всi розв’язки однорiдної "системи"

10x1 3x2 2x3 = 0:

(12)

Роз’вязання. Немає потреби для застосування матриць. Розв’яжемо для базисної змiнної x1 у термiнах вiльних змiнних. Загальний розв’язок є x1 = 0:3x2 + 0:2x3, з вiльними змiнними x2 i x3. Як вектор, загальний розв’язок є

~x =2 x2	3	=2				x2	3 =		2	x2	3	+ 2	0 3
x1	5	4	0:3x2 + 0:2x3				5		4	0:3x2	5	4	0:2x3	5
4 x3			2	0:3	3	x3		:2		0			x3		(13)
		=x2		1		+ x3	2	0	3	(з вiльними x2; x3)
			4	0	5		4	1	5

Цi обчислення показують, що кожний розв’язок (12) є лiнiйна комбiнацiя векторiв ~u i ~v, як показано у (13). Таким чином, множина розв’язкiв є L(~u; ~v). Оскiльки нi ~u нi ~v не виражається через iнший, то множина розв’язкiв є площина, яка проходить через початок координат. Дивись рисунок 7.

	Рисунок 7.
	Приклади 8 i 9 iлюструють факт, що множина розв’язкiв однорiдного рiвняння A~x =
~	може завжди бути виражена явно як лiнiйна оболонка L(~u1; : : : ; ~vp) для пiдходящих
0

векторiв ~ ~ . Якщо розв’язком є тiльки нуль-вектор, то множина розв’язкiв є ~ u1; : : : ; vp L(0) =

23

~	~	має тiльки одну вiльну змiнну, то множина розв’язкiв є пряма,
0. Якщо рiвняння A~x = 0

яка проходить через початок, як на рис.6. Площина, яка проходить через початок, як на

рис.7, iлюструє хороший явний образ для множини розв’язкiв ~ ~, коли iснують двi

Ax = 0

вiльних змiнних. Зауважимо, разом з тим, що подiбна фiгура може бути використана для

представлення ~ ~ навiть, коли ~ i ~ не виникають як розв’язки ~ ~.

L(u; v) u v Ax = 0

Параметрична векторна форма

Вихiдне рiвняння (12) для площини у ррикладi 9 є неявним описом площини. Розв’я- зуючи це рiвняння у пiдсумку знайдено явний опис площини як множини, породженої векторами ~u i ~v. Рiвняння (13) називається параметричним векторним рiвнянням площини. Iнодi таке рiвняння записують як

~x = s~u + t~v (s; t належать R)

наголошуючи, що параметри змiнюються над всiма дiйсними числами. У прикладi 1, рiвняння ~x = x3~v (з вiльною x3), або ~x = t~v (де t належить R), є параметричне векторне рiвняння прямої. Завжди, коли множина розв’язкiв описана явно з векторами, як у Прикладах 1 i 2, ми говоримо, що розв’язок є у параметричнiй векторнiй формi.

Розв’язки неоднорiдних систем

Коли неоднорiдна лiнiйна система має багато розв’язкiв, то її загальний розв’язок може бути описаний у параметричнiй векторнiй формi у виглядi суми одного з її розв’язкiв та довiльної лiнiйної комбiнацiї векторiв, якi задовольняють вiдповiдну однорiдну систему.

ПРИКЛАД 10. Описати всi розв’язки ~ ~ , де

Ax = b

A =	2	3	2	4 3	i	~b =	2 1 3	:
		3	5	4			7
	4 6		1	8 5			4 4 5

Роз’вязання. Тут A є матриця коефiцiєнтiв з прикладу 8. Рядковi перетворення над

~
[A jb] дають																		8
2	3	2	4			1		3 2 0 1						4		2 3;			x2		4	= 2;
													0
	3	5		4		7					1 0			3		1		<	x1		3 x3 = 1;
	6	1		8		4					0 0			0		0					0	= 0:
4			4					5		4						5		:				~
Тому x1 = 1 +			3 x3, x2 = 2; i x3 є вiльною. Як вектор, загальний розв’язок A~x = b має
форму
~x = 2 x2			3 =		2				4	2	3 = 2			2	3 + 2		4	0	3 = 2 2 3		+ x3	4
							1 +										3					2 0 3:
		x1	5 4						3 x3		5 4			1				x3	5 4	1		3
	4 x3									x3				0 5 4				x3		0 5		4 1 5
Рiвняння ~x = ~p + x3~v, або, записуючи t як загальний параметр,
								~x = ~p + t~v						(t		належить			R)			(14)
описує множину розв’язкiв											~	у параметричнiй векторнiй формi. Нагадаємо з при-
								A~x = b
															~
кладу 8, що множина розв’язкiв рiвняння A~x = 0 має параметричне векторне рiвняння
								~x = t~v;				(де		t		належить			R)			(15)
															~
[з однаковим ~v як у (14)]. Тому розв’язки A~x = b отримуються додаванням вектора ~p до
		~																			~
розв’язкiв A~x = 0. Вектор ~p сам є одним з частинних розв’язкiв A~x = b, який вiдповiдає
t = 0 у (14)].

24

Описуючи множину розв’язкiв ~ ~ геометрично, ми можемо думати про вектор-

Ax = b

доданок як про паралельне перенесення. Для заданих ~v i ~p з R2 або R3, ефект додавання

~ до ~ є рух ~ у паралельному напрямi до прямої, яка проходить через ~ i ~. Ми говоримо, p v v p 0

що вектор ~v паралельно перенесено на ~p у ~v + ~p. Дивись рис.8.

Рисунок 8. Додавання ~p до ~v паралельно переносить ~v на ~v + ~p.

Якщо кожна точка прямої L у R2 або R3 паралельно переноситься на вектор ~p, то результатом є пряма паралельна до L. Дивись рис.9.

Рисунок 9. Паралельне перенесення прямої.

Припустимо, що є пряма, яка проходить через ~ i ~ , описана у рiвняннi (15). Додаючи

L 0 v

~p до кожної точки на L отримуємо перенесення прямої, описане рiвнянням (14). Зауважимо, що ~p лежить на прямiй (14). Ми називаємо (14) рiвнянням прямої, яка проходить

		~
через вектор ~p паралельно до ~v. Тому множина розв’язкiв рiвняння A~x = b є пряма,
		~
яка проходить через вектор ~p, паралельно до множини розв’язкiв A~x = 0. Рисунок 10
iлюструє цей випадок.
	~	Рисунок 10. Паралельнi
		~
множини розв’язкiв A~x = b i A~x = 0.
~	~	показанi на рис. 10 узагаль-
Вiдношення мiж множинами розв’язкiв A~x = b i A~x = 0

нюються на будь-яке сумiсне рiвняння ~ ~ , хоча множина розв’язкiв не буде пряма,

Ax = b

коли iснує декiлька вiльних змiнних. Наступна теорема дає точне формулювання.

ТЕОРЕМА 6.

25

Припустимо, що рiвняння	~	є сумiсним	для деякого заданого	~	i нехай ~p
	A~x = b			b

буде його частинним розв’язком. Тодi загальний розв’язок даного рiвняння є множина всiх векторiв виду w~ = ~p + ~v, де ~v є будь-яким розв’язком вiдповiдного однорiдного

рiвняння ~ ~.

Ax = 0

Теорема 6 говорить, що коли ~ ~ має розв’язок, то множина розв’язкiв отримана пе-

Ax = b

ренесенням множини розв’язкiв ~ ~, використовуючи будь-який частинний розв’язок

Ax = 0

~ рiвняння ~ ~ для переносу. Рисунок 11 iлюструє випадок, коли iснує двi вiльних p Ax = b

змiнних. Навiть коли наш мислимий образ множини розв’язкiв сумiсної системи ~ ~ Ax = b

(з ~ 6 ~) є одне з: єдина ненульова точка або пряма або площина, що не проходить через b = 0

початок.

	Рисунок 11.
	~	~
Паралельнi множини розв’язкiв A~x = b i A~x = 0.
Зауваження: Теорема 6 i рис.6 стосуються тiльки рiвняння		~
		A~x = b, яке має хоча
б один ненульовий розв’язок. Коли	~
	A~x = b не має розв’язку, то множина розв’язкiв є

порожною.

Наступний алгоритм обчислень в загальних рисах показано у прикладах 11, 12 i 13.

Запис множини розв’язкiв (сумiсної системи) у параметричнiй векторнiй формi

1.Рядкова редукцiя розширеної матрицi до зведеної ступiнчатої форми.

2.Вираження кожної базисної змiнної у термiнах будь-яких вiльних змiнних, якi є у рiвняннi.

3.Запис типового розв’язку ~x як вектора, координати якого залежать вiд вiльних змiнних, якi набувають довiльних значень.

4.Розклад ~x в лiнiйну комбiнацiю векторiв (з чисельними координатами), використовуючи вiльнi змiннi як параметри.

Лiнiйна незалежнiсть

Системи однорiдних лiнiйних рiвняннь можуть бути вивченi з iншої точки зору, записавши їх як векторнi рiвняння. На цьому шляху увага пересувається вiд невiдомих

розв’язкiв системи ~ ~ до векторiв, якi з’являються у векторних рiвняннях.

Ax = 0

Наприклад, розглянемо рiвняння

x1	2	2	3	+ x2	2	5	3	+ x3	2	1	3	=	2	0	3	:	(16)
		1				4				2				0
	4 3 5				4 6 5				4 1 5				4 0 5

26

Це рiвняння звичайно має тривiальний розв’язок x1 = x2 = x3 = 0. Проте головним висновком тут є те, що тривiальний розв’язок є тiльки один.(Перевiрте це!)

ОЗНАЧЕННЯ.

Iндексована (лiнiйно упорядкована) множина векторiв f~v1; ~v2; : : : ; ~vpg у Rn називається лiнiйно незалежною, якщо векторне рiвняння

~ ~ ~ ~

x1v1 + x2v2 + : : : + xpvp = 0

має тiльки один тривiальний розв’язок. Множина f~v1; ~v2; : : : ; ~vpg називається лiнiйно залежною, якщо iснують ваги c1; c2; : : : ; cp серед яких не всi рiвнi нулю, такi, що

~	(17)
c1~v1 + c2~v2 + : : : + cp~vp = 0:

Рiвнiсть (17) називається вiдношенням лiнiйної залежностi мiж ~v1; ~v2; : : : ; ~vp, коли не всi ваги рiвнi нулю.

Коротше, ми можемо говорити, що вектори ~v1; ~v2; : : : ; ~vp лiнiйно залежнi, коли ми маємо на увазi, що f~v1; ~v2; : : : ; ~vpg є лiнiйно залежною множиною. Ми використовуємо аналогiчний термiн для лiнiйно незалежних множин.

З наведеного означення випливає, що iндексована множина векторiв 1 є однiєю з двох:

лiнiйно залежною або лiнiйно незалежною.					5	3, ~v3	=	2	1	3	:
ПРИКЛАД 11. Нехай ~v1 =	2	2	3, ~v2 =	2
	4	1	5	4	4	5		4	2	5
		3			6				0

a). Встановити, чи є множина f~v1; ~v2; ~v3g лiнiйно незалежною.

б). Якщо можливо, знайти вiдношення лiнiйної залежностi мiж ~v1; ~v2; ~v3.

Роз’вязання. a). Ми повиннi встановити чи iснує нетривiальний розв’язок рiвняння

						~		(18):
		x1~v1 + x2~v2 + x3~v3 = 0
Рядковi перетворення над асоцiйованою розширеною матрицею показують, що
2 2	5	1	0 3	2 0	3	3	0 3	:
1	4	2	0	1	4	2	0
4 3	6	0	0 5 4 0		0	0	0 5

Ясно, що x1 i x2 є базиснi змiннi i x3 є вiльною. Кожне ненульове значення x3 визначає нетривiальний розв’язок рiвняння (18). Тому ~v1; ~v2; ~v3 утворюють лiнiйно залежну множину векторiв.

б). Щоб знайти вiдношення лiнiйної залежностi мiж ~v1;~v2; ~v3 доповнимо рядкову редукцiю розширеної матрицi i запишемо нову систему:

2 0	1	1	0	3;	8	x2	+	x3	= 0;
1	0	2	0		x1			2x3	=	0;
0	0	0	0	5	<			0	=	0:
4					:

Тому x1 = 2x3; x2 = x3 i x3 є вiльною. Виберемо будь-яке ненульове значення для x3 – скажiмо, x3 = 5. Тодi x1 = 10 i x2 = 5. Пiдставимо цi значення у (18) i отримаємо

~ ~ ~ ~

10v1 5v2 + 5v3 = 0:

Це є одне з можливих вiдношень лiнiйної залежностi мiж ~v1; ~v2 i ~v3.

1Часто iндексовану множину векторiв називають системою векторiв.

27

Лiнiйна незалежнiсть матричних стовпцiв

Припустимо, що ми починаємо з матрицi A = [~a1 ~a2 : : : ~an] замiсть множини векторiв.

Матричне рiвняння ~ ~ може бути записане як

Ax = 0

~ ~ ~ ~

x1a1 + x2a2 + : : : + xnan = 0:

Кожному вiдношенню лiнiйної залежностi мiж стовпцями A вiдповiдає нетривiальний

розв’язок рiвняння ~ ~. Тому ми маємо наступний важливий факт.

Ax = 0

~	має
Стовпцi матрицi є лiнiйно незалежними тодi i тiльки тодi, коли рiвняння A~x = 0
тiльки тривiальний розв’язок.

	2	0	1	4	3
ПРИКЛАД 12. Встановити, чи є стовпцi матрицi A =		1	2	1		лiнiйно незалежни-
ми.	4	5	8	0	5

				~
Роз’вязання. Розглядаючи A~x = 0, застосуємо рядкову редукцiю розширеної матрицi:
2 1	2	1		3 2 0	1	4		0	3 2 0	1	4		0 3	:
			0
0	1	4	0	1	2	1		0	1	2	1		0
4 5	8	0	0 5 4 0		2	5		0 5 4 0		0	13		0 5

Тепер ясно, що iснує три базисних змiнних i вiльних змiнних немає. Тому рiвняння

~ ~ має тiльки тривiальний розв’язок i стовпцi матрицi є лiнiйно незалежними.

Ax = 0 A

Множини з одного або двох векторiв

Множина, яка мiстить тiльки один вектор, – скажемо ~v - є лiнiйна незалежною тодi i тiльки тодi, коли ~v ненульовий вектор. Це слiдує з того, що векторне рiвняння x1~v =

~	має тiльки тривiальний розв’язок, коли ~v	~	Множина,	яка мiстить тiльки один
0		6= 0:
			~ ~
нульовий вектор є лiнiйно залежною тому, що рiвняння x10 = 0 має багато нетривiальних

розв’язкiв.

Наступний приклад буде пояснювати природу лiнiйної залежностi множини з двох векторiв.

ПРИКЛАД 13.Встановити спостереженням, чи є такi вектори лiнiйно незалежними:

a). ~v1	=	1 ,	~v2	=	2	;	б). ~v1	=	2 , ~v2 =	2	:
		3			6				3	6

Роз’вязання. a) Замiтимо, що ~ кратний до ~ , а саме, ~ ~ . Тому ~ ~ ~, v2 v1 v2 = 2v1 2v1 + v2 = 0

яка показує що множина f~v1; ~v2g є лiнiйно залежною.

б) Вектори ~v1 i ~v2 не є кратними один iншому. Чи можуть вони бути лiнiйно залежними? Припустимо, що c i d задовольняють рiвняння

~ ~ ~

cv1 + dv2 = 0:

Якщо c 6= 0, то ми можемо розв’язати ~v1 у термiнах ~v2, а саме, ~v1 = ( dc )~v2. Цей результат неможливий тому, що ~v1 не є кратним до ~v2. Тодi c повинно бути нулем. Аналогiчно, d повинно бути нулем. Тому f~v1; ~v2g є лiнiйно незалежна множина.

Аргументи у прикладi 13 показують, що ви можете завжди оцiнити спостереженням, коли множина з двох векторiв є лiнiйно незалежною. Рядковi перетворення не є необхiдними. Просто перевiряють чи є один з векторiв кратним iншому. (Цей тест пiдходить тiльки для множин з двох векторiв.)

Множина з двох векторiв f~v1; ~v2g є лiнiйно залежною, якщо хоча б один з векторiв є кратним до iншого. Множина є лiнiйно незалежною тодi i тiльки тодi, коли жоден з векторiв не є кратним до iншого.

28

У геометричнiй термiнологiї, два вектори є лiнiйно залежними тодi i тiльки тодi, коли вони лежать на однiй прямiй, яка проходить через початок. Наступний рисунок 12 показує вектори з прикладу 13.

Лiнiйно залежнi Лiнiйно незалежнi

Рисунок 12.

Множини з двох або бiльше векторiв

Доведення наступної теореми подiбне до розв’язання прикладу 13. Деталi його можна знайти у [1, §28, стор. 286,287].

ТЕОРЕМА 7.

Характеристика лiнiйно залежних множин

Iндексована множина S = f~v1; ~v2; : : : ; ~vpg з двох або бiльше векторiв є лiнiйно залежною тодi i тiльки тодi, коли хоча б один з векторiв у S є лiнiйною комбiнацiєю iнших.

Фактично, якщо	~	(з j > 1) є лiнiйною
	S є лiнiйно залежною i ~v1 6= 0, то деякий ~vj

комбiнацiєю попереднiх векторiв ~v1; ~v2; : : : ; ~vj 1.

Застереження: Теорема 7 не говорить, що кожний вектор у лiнiйно залежнiй множинi повинен бути лiнiйною комбiнацiєю попереднiх векторiв.

2

3

2

3

31

ПРИКЛАД 14 Нехай ~u = 4 1 5 i ~v = 4 6 5: Описати множину породжену ~u i ~v i

00

пояснити чому вектор w~ належить L(~u; ~v) тодi i тiльки тодi, коли f~u; ~v; w~ g є лiнiйно залежною.

Роз’вязання. Вектори ~u i ~v є лiнiйно незалежними тому, що нi один з векторiв не є кратним iншого, i вони породжують площину у R3. Фактично L(~u; ~v) є x1x2-площиною (з x3 = 0). Якщо w~ є лiнiйною комбiнацiєю ~u i ~v, то f~u; ~v; w~ g є лiнiйно залежною, за теоремою 7. Навпаки, припустимо, що множина f~u; ~v; w~ g є лiнiйно залежною. За теоермою 7, деякий вектор у f~u; ~v; w~ g є лiнiйною комбiнацiєю попереднiх векторiв (оскiльки

~	, оскiльки ~v не кратний до ~u. Тому w~	є у L(~u; ~v).
~u 6= 0). Цей вектор повинен бути w~
Дивись рис.13.

Лiнiйна залежнiсть;	Лiнiйна незалежнiсть;
w~ у Spanf~u; ~vg	w~ не у Spanf~u; ~vg

Рисунок 13. Лiнiйна залежнiсть у R3.

Приклад 4 узагальнюється для будь-якої множини f~u; ~v; w~ g векторiв з R3 при лiнiйно незалежних ~u i ~v так: Множина f~u; ~v; w~ g векторiв з R3 буде лiнiйно залежною тодi i тiльки тодi, коли вектор w~ належить площинi, породженiй лiнiйно незалежними векторами ~u i ~v.

29

Наступнi двi теореми описують спецiальнi випадки лiнiйної залежностi множини векторiв i якi часто використовуються далi.

ТЕОРЕМА 8.

Якщо множина мiстить бiльше векторiв нiж iснує координат у кожного вектора, то множина є лiнiйно залежною. Тому, будь-яка множина f~v1; ~v2; : : : ; ~vpg у Rn є лiнiйно залежною, якщо p > n.

ДОВЕДЕННЯ. Нехай f~ ~ ~ g. Тодi є матрицею i рiвнянню ~ ~ A = v1; v2; : : : ; vp A n p Ax = 0

вiдповiдає система n рiвнянь з p невiдомими. Якщо p > n, то iснує бiльше змiнних нiж

~	має нетривiальний розв’язок
рiвнянь. Тому повинна iснувати вiльна змiнна. Отже, A~x = 0
i стовпцi A є лiнiйно залежними. Дивись рис.14 для матричної версiї цiєї теореми.

p

23

	4						5
n

Якщо p > n, то стовпцi є лiнiйно залежними.

РИСУНОК 15.

Застереження: Теорема 8 нiчого не говорить про випадок, коли число векторiв у множинi не перевищує числа координат у кожного вектора.

ПРИКЛАД 15. Вектори	2	,	4	i	2	є лiнiйно залежними за Теоремою 8,
	1		1		2

тому що iснує три вектори у множинi i iснує тiльки двi координати у кожного вектора. Зауважимо, разом з тим, що нi один вектор не є кратним до iншого з векторiв. Дивись Рис.4.

Рисунок 15. Лiнiйно залежна множина у R2.

ТЕОРЕМА 9.

Якщо множина S = f~v1; ~v2; : : : ; ~vpg у Rn мiстить нуль вектор, то вона є лiнiйно залежною.

									~
ДОВЕДЕННЯ Перенумерувавши номери ми можемо вважати, що ~v1 = 0. Тодi рiвнiсть
						~
1~v1 + 0~v2 + : : : + 0~vp = 0 показує, що S є лiнiйно залежною.
ПРИКЛАД 16. Встановити спостереженням, чи є дана множина лiнiйно залежною.
a)	2 7 3		; 2 0	3;	2 1	3; 2 1 3; b.	2 3	3; 2 0	3; 2 1 3;
		1	2		3	4	2	0	1
	4 6 5 4 9 5 4 5 5 4 8 5						4 5 5 4 0 5 4 8 5
c.	2 4 3; 2			6 3:
	6	2	7 6	3	7
		6		9
	6	10	7 6	15	7
	4		5 4		5

Роз’вязання.