ЛЕКЦИЯ №44
15.4 Теорема Гаусса в дифференциальной форме
С помощью интегральной
теоремы Гаусса нельзя определить, как
связан исток линий
в данной точке поля с плотностью свободных
зарядов в той же точке поля. Поэтому
переходят к записи теоремы Гаусса в
дифференциальной форме:
(15.16)
Исток линий
в данной точке поля определяется
величиной плотности свободных зарядов
в этой точке (рис. 15.4).
Если среда однородна и изотропна, т.е. a = const, то можно записать:
(15.17)
или:
(15.18)
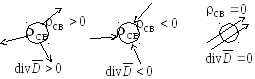
Рис. 15.4. К пояснению
истока линий вектора
Истоком вектора
в отличие от истока вектора
являются не только свободные, но и
связанные заряды.
С другой стороны известно, что
С учетом этого
Или
(15.19)
Уравнение (15.19) называется уравнением Пуассона. Частный вид уравнения Пуассона при св = 0, называется уравнением Лапласа
.
Эти два уравнения являются основными уравнениями электростатики. Уравнение Пуассона выражает связь между частными производными второго порядка от в любой точке поля и плотностью свободных зарядов в этой точке поля.
Решение уравнения Пуассона в общем виде можно найти следующим образом. Положим, что в объеме V есть объемные , поверхностные и линейные заряды. Эти заряды представим в виде совокупности точечных зарядов: dV, ds и dl, где dV – элемент объема, ds – элемент заряженной поверхности, dl – элемент длинны заряженной оси. Составляющая потенциала d в некоторой точке пространства, удаленной от dV на расстояние r, в соответствии с формулой (15.15) равна
Аналогично можно определить составляющие потенциала от поверхностного и линейного зарядов
и
.
Полное значение определяется как сумма (интеграл) составляющих потенциала от всех зарядов поля:
(15.20)
В формуле (15.20) , и есть функции радиуса r, которые практически определить очень трудно. Предполагается, что потенциал на бесконечности равен нулю и заряды, создающие поля распределены в ограниченной области (иначе интеграл может оказаться расходящимся).
15.5. Граничные условия
Под граничными условиями понимают условия, которым подчиняется поле на границах раздела сред с различными электрическими свойствами.
При интегрировании уравнения Лапласа (или Пуассона) в решение входят постоянные интегрирования. Их определяют из граничных условий.
В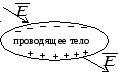
проводящем теле, находящемся в магнитном
поле, вследствие явления электростатической
индукции происходит разделение зарядов
(рис. 15.5).
Рис. 15.5. разделение зарядов в проводящем теле
Все точки тела будут иметь один и тот же потенциал (иначе появилось бы упорядоченное движение зарядов). Поверхность тела эквипотенциальна. Вектор напряженности внешнего поля в любой точке поверхности подходит к ней под прямым углом. Внутри проводящего тела напряженность равна нулю, так как внешнее поле компенсируется полем зарядов, расположившихся на поверхности тела.
На границе раздела проводящего тела и диэлектрика при отсутствии тока по проводящему телу выполняются два условия:
1. Отсутствует тангенциальная (касательная к поверхности) составляющая напряженности поля
(15.21)
2. Вектор электрического
смещения
в любой точке диэлектрика, непосредственно
примыкающей к поверхности проводящего
тела, численно равен плотности заряда
на поверхности проводящего тела в этой
точке:
(15.22)
На границе раздела двух диэлектриков с различными диэлектрическими проницаемостями выполняются следующие условия:
1. Тангенциальные составляющие напряженности поля равны:
Et1 = Et2. (15.23)
2. Нормальные составляющие электрической индукции равны:
Dn1 = Dn2. (15.24)
Уравнения Лапласа и Пуассона являются уравнениями в частных производных, которые в общем случае имеют множество линейно независимых друг от друга решений. Выбор единственного решения, удовлетворяющего конкретной задаче, производят с помощью граничных условий.
15.6. Общая характеристика задач электростатики
и методов их решения
В зависимости от того, что задано и что необходимо определить, задачи электростатики можно подразделить на три типа.
1. По заданному закону распределения потенциала в пространстве (x, y, z) найти распределение свободных зарядов, вызвавших поле.
Такого рода задачи можно решать с помощью уравнений Пуассона. Это наиболее простой тип задач.
2. Задан закон распределения свободных зарядов в пространстве в функции координат своб(x, y, z). Требуется найти закон изменения потенциала в пространстве (x, y, z).
Эта задача является обратной по отношению к первой и значительно сложнее ее.
Принципиально задача состоит в решении уравнения Пуассона относительно , т.е. в решении дифференциального уравнения второго порядка в частных производных.
Задачи первого и второго типа на практике встречаются редко, чаще приходится иметь дело с задачами третьего типа.
3. Известны потенциалы (или полные заряды) и геометрия тел, создающих поле. Требуется найти закон изменения напряженности или потенциала во всех точках поля.
Если среда, в которой создано поле, является неоднородной, то ее подразделяют на однородные области, и решение уравнения Лапласа производят для каждой области отдельно. Основная трудность задачи состоит в том, что хотя полные заряды тел и известны, но плотность распределения зарядов на отдельных участках заряженного тела неизвестна. Решения уравнений Лапласа для отдельных областей должны быть согласованы друг с другом: на границе раздела двух сред с различными диэлектрическими проницаемостями должны выполняться граничные условия.
Задачи третьего типа можно решать аналитически, графически либо путем моделирования.
15.7. Поле заряженной оси
Под заряженной осью понимают тонкий, теоретически бесконечно длинный металлический проводник.
Под линейной плотностью заряда понимают заряд, приходящийся на единицу длины оси.
Пусть диэлектрическая проницаемость окружающей среды равна a.
Для нахождения напряженности поля в некоторой точке, удаленной на расстояние r от оси, проведем через точку цилиндрическую поверхность так, чтобы ее ось совпала с заряженной осью (рис. 15.6).
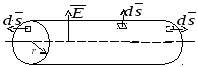
Рис. 15.6. К определению поля заряженной оси
Используем теорему
Гаусса, которая применима к замкнутой
поверхности (боковая поверхность
цилиндра и два его основания). Поток
вектора
имеется только через боковую поверхность.
Направление
и
на боковой поверхности в каждой точке
совпадают, поэтому
или
(15.25)
Напряженность в поле заряженной оси изменяется обратно пропорционально расстоянию r точки от оси.
(15.26)
Потенциал изменяется по экспоненциальному закону.
Электрическая емкость определяется как отношение заряда к разности потенциалов между телами. Рассчитаем емкость двух соосных цилиндров (рис. 15.7).
Рис. 15.7. Разрез двух соосных цилиндров
Напряжение между поверхностями цилиндров
.
Емкость цилиндрического конденсатора будет равна
(15.27)
15.8. Поле двух параллельных заряженных осей
Пусть одна ось имеет линейный заряд + , а другая – - . Возьмем в поле некоторую произвольную точку М (рис. 15.8).
Результирующая
напряженность поля в точке М
равна
геометрической сумме напряженностей
от обоих зарядов. Потенциал – функция
скалярная, и он равен сумме потенциалов
от каждой оси
(15.28)
У
равнением
эквипотенциали в поле двух заряженных
осей является выражение b/a
= const, т.е. эквипотенциаль представляет
собой совокупность точек, отношение
расстояний которых до двух заданных
точек есть величина постоянная. Из
геометрии известно, что такой совокупностью
точек является окружность. Для ее
построения соединим точку М
с осями. Проведем биссектрису внутреннего
(aMb)
и внешнего (pMa)
углов. Точки 1 и 2 пересечения биссектрис
с линией, проведенной через заряженные
оси, и точка М
будут тремя точками окружности. Для
нахождения положения центра окружности
(точки О)
разделим пополам расстояние между
точками 1 и 2.
Рис. 15.8. Поле двух заряженных осей
Рассмотрим поле двухпроводной линии (рис. 15.9).
Рис. 15.9. К рассмотрению поля двухпроводной линии
Заряды проводов по поверхности распределены с неодинаковой плотностью.
Задача о поле двухпроводной линии может быть сведена к задаче о поле двух заряженных осей.
Пусть заряженные оси будут расположены в точках m и n. Из условия симметрии они удалены на одинаковое расстояние x от геометрических осей проводов О2 и О1.
Для точки 1 отношение
b/a
будет
,
для точки 2 –
.
Из равенства
получим
.
(15.29)
Знак минус перед радикалом соответствует положению точки n, знак плюс – точке m.
Точки m и n называют электрическими осями проводов. Их можно получить геометрическим построением. Проводится линия, параллельная линии, соединяющей оси проводов и касательная к поверхности проводов. Через точки касания поводится окружность диаметром d. Пересечение этой окружности с линией соединяющей оси проводов даст положение электрических осей.
Определим емкость двухпроводной линии
;
;
;
.
(15.30)