11-а, Решение интегралов

Решение интегралов. Рассказываем, как решать интегралы.

Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое. Решение интегралов (интегрирование) есть операция обратная диференциированию. Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему. В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .

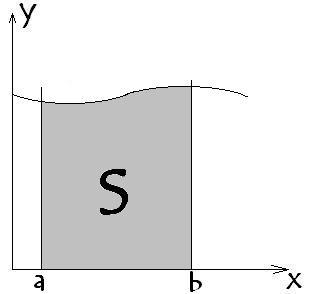
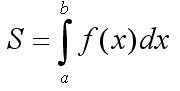Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b. Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим: 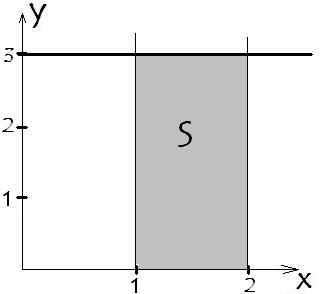Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3. Попробуем решить тоже самое не прибегая к построению, используя интегрирование: 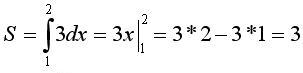Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными. Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной. F(x) – первообразная. Дифференцируя первообразую, мы получим исходное подинтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференциируем полученный ответ и сравниваем с исходным выражением. Основные функции и первообразные для них приведены в таблице:

Таблица первообразных для решения интегралов

Основные приемы решения интегралов: Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду. Сначала следует запомнить основные свойства интегралов:

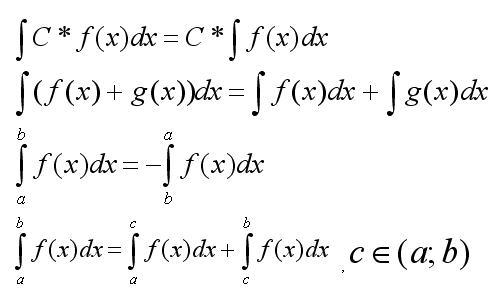
Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные примеры решения интегралов. Приемы будет даны для общего ознакомления без примеров решения, чтобы не перегружать статью. Нужно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.

Основные приемы решения интегралов

1. Замена переменной. 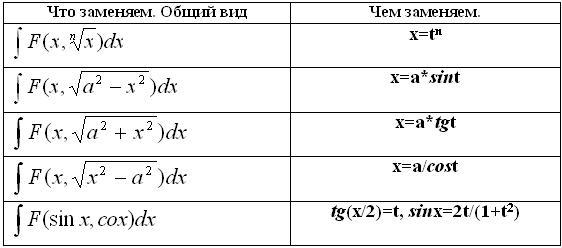Для выполнения данного приема потребуется хороший навык нахождения производных.

2. Интегрирование по частям. Пользуются следующей формулой. 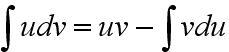Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.

3. Интегрирование дробно-рациональных функций.  - разложить дробь на простейшие  - выделить полный квадрат.  - создать в числителе дифференциал знаменателя.

4. Интегрирование дробно-иррациональных функций.  - выделить под корнем полный квадрат  - создать в числителе дифференциал подкоренного выважения. 5. Интегрирование тригонометрических функций.  При интегрировании выражений вида применяет формулы разложения для произведения. Для выражений  m-нечетное, n –любое, создаем d(cosx). Используем тождество sin²+cos²=1 m,n – четные, sin²x=(1-cos2x)/2 и cos²x=(1+cos2x)/2 Для выражений вида:  - Применяем свойство tg²x=1/cos²x – 1

1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первобразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию. 2. Отработать использование таблицы первообразных и основным свойства интегралов. Необходимо научиться пользоваться таблицей первообразных. По множеству функций первообразные найдены и занесены в таблицу. Если мы имеем интеграл, которые есть в таблице, можно сказать, что он решен. 3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя. Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференциируем полученное выражение и сравниваем с исходным интегралом. Отработаем основные моменты на нескольких примерах:

Примеры решения интегралов

Пример 1: Решить интеграл: 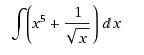Интеграл неопределенный. Находим первообразную. Для этого интеграл суммы разложим на сумму интегралов. Каждый из интегралов табличного вида. Смотрим первообразные по таблице. Решение интеграла: Проверим решение(найдем производную):

Пример 2. Решаем интеграл Интеграл неопределенный. Находим первообразную. Сравниваем с таблицей. В таблице нет. Разложить, пользуясь свойствами, нельзя. Смотрим приемы. Наиболее подходит замена переменной. Заменяем х+5 на t⁵. t⁵ = x+5 . Получаем. Но dx нужно тоже заменить на t. x= t⁵ - 5, dx = (t⁵ - 5)’ = 5t⁴. Подставляем: Интеграл из таблицы. Считаем: Подставляем в ответ вместо t , Решение интеграла:

Пример 3. Решение интеграла: 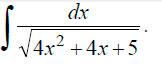Для решения в этом случае необходимо выделить полный квадрат. Выделяем:

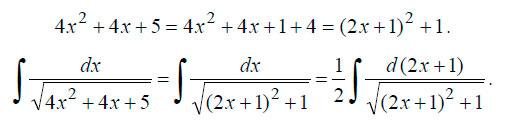
В данном случае коэфециент ½ перед интегралом получился в результате замены dx на ½*d(2x+1). Если вы найдете производные x’ = 1 и ½*(2x+1)’= 1, то поймете почему так. В результате мы привели интеграл к табличному виду. Находим первообразную. 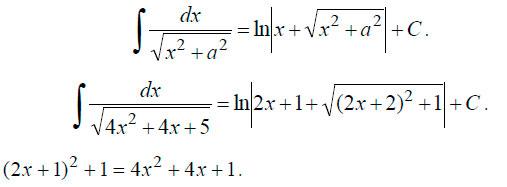В итоге получаем: