Теорія автоматичного керування» Конспект лекцій з дисципліни

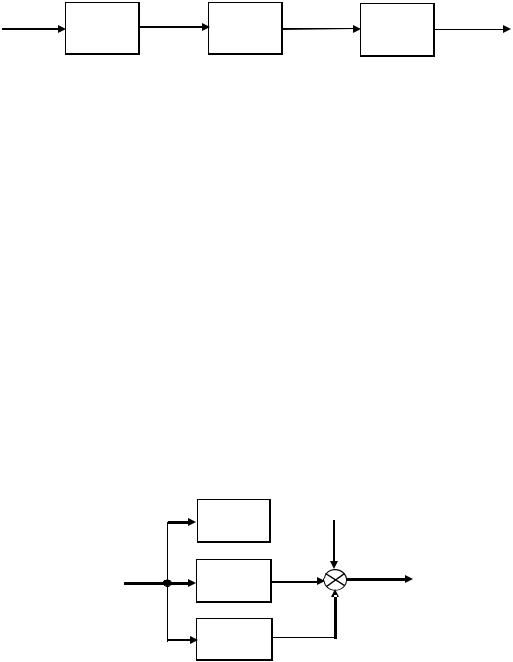
	X1(p)			X2(p)			X3(p)		X4(p)
		W1(p)				W2(p)
								W3(p)

Рис. 1.13

Значення функцій передачі окремих ланок:

W

( p)

X2

( p)

;

W

( p)

X3

( p)

;

W

( p)

X4

( p)

.

(1.24)

1

X1

( p)

2

X2

( p)

3

X3

( p)

Еквівалентна функція передачі всієї структури при послідовному з’єднанні

Wåêâ ( p)	X4	( p)	.	(1.25)
	X1
		( p)

Якщо чисельник та знаменник одночасно помножити на Х2(р), Х3(р), то отримаємо:

Wåêâ ( p)

X4 ( p)

X2 ( p)

X3 ( p)

X2 ( p)

X3 ( p)

X4 ( p)

W1 ( p) W2 ( p) W3 ( p), ,

(1.26)

X1 ( p)

X2 ( p)

X3 ( p)

X1 ( p)

X2 ( p)

X3 ( p)

тобто, при послідовному з’єднанні динамічних ланок еквівалентна функція передачі такої структури дорівнює добутку функцій передачі окремих елементів:

n

Wåêâ ( p) Wi ( p) . (1.27)

i 2

При паралельному з’єднанні (прямий зв’язок) структурна схема виглядає як на рис. 1.14:

				X2(p)
		W1(p)
	X1(p)			X3(p)	+	X5(p)
		W2(p)
			+		+

X4(p)

W3(p)

Рис. 1.14

Вихідний сигнал структури являє собою суму вихідних сигналів окремих ланок:

Х5(р) = Х2(р) + Х3(р) + Х4(р),

(1.28)

а еквівалентна функція передачі такої структури:

W

( p) X5 ( p)

X2 ( p) X3 ( p) X4 ( p)

X2 ( p) X3 ( p) X4 ( p)

екв

X1( p)

X1( p)

X1( p) X1( p) X1( p)

(1.29)

W1( p) W2 ( p) W3 ( p),

іншими словами при паралельному з’єднанні еквівалентна функція передачі дорівнює сумі функцій передачі окремих елементів:

n

Wекв( p) Xi ( p) . (1.30)

i 2

При зворотному зв’язку, де одна ланка охоплює зворотним зв’язком іншу, структурна має вигляд, зображений на рис. 1.15

X1(p)	X2(p)					X3(p)
			W1(p)
+	±
	Xзз(p)		Wзз(p)

Рис. 1.15

Згідно з наведеною схемою Х3(р) = Х2(р) W1(p), Хзз(р) = Х3(р) Wзз(p), а Х2(р)= Х1(р)± Хзз(р), «плюс» для додатного, «мінус» для від’ємного зворотного

зв’язку. В останньому випадку нижній сектор умовного позначення суматора заштриховують.

Еквівалентна функція передачі такої структури :

	Wеквзз ( p)	X3 ( p)		X3 ( p)	.
		X1( p)		X2 ( p) Хзз( р)

Поділивши чисельник і знаменник на Х3(р), отримаємо:

Х3 ( р)

Х3 ( р)

W1( p)

зз

Х2 ( р)

Х2 ( р)

Wекв( p)

.

Хзз( р)

Хзз( р)Х3 ( р)

1 W1( p)W33 ( p)

1

Х2 ( р)

1

Х2 ( р)Х3

( р)

(1.31)

(1.32

В останній формулі знак «плюс» вибирається для від’ємного зворотного зв’язку, а «мінус» для додатного. Таким чином, при наявності зворотного зв’язку еквівалентна функція передачі являє собою дріб, в чисельнику якого записана функція передачі ланки, яка охоплена зворотним зв’язком, а у знаменнику – одиниця плюс-мінус добуток функцій передачі обох ланок.

1.2.4Різновиди функцій передачі систем керування.

Розглянемо просту одноконтурну систему, яка

керування та керуючої частини.

f(p) Wзб(p)

Y(p)	ε(p) Wкч(p)	U(p)	Wоб(p)

Рис. 1.16

складається з об’єкта

X(p)

На схемі рис 1.16 позначено:

Wзб(p) – функція передачі об’єкта керування по каналу збурення; Wоб(p) – функція передачі об’єкта керування по каналу керування; Wкч(p) – функція передачі керуючої частини;

f(p) – збурення;

Y(p) – завдаючий вплив (завдання); U(p) – керуючий вплив;

Х(р) – координата стану об’єкта керування; ε(р) = Y(p)-Х(р) – помилка керування;

В запропонованій системі можна виділити дві вхідних дії: завдання Y(p) та збурення f(p) і дві вихідних координати – координату стану об’єкта Х(р), помилку керування ε(р).

Функція передачі за визначенням може бути записана тільки для однієї вхідної та однієї вихідної величини, при тому вважають, що інші вхідні величини відсутні, тобто дорівнюють нулю.

Будемо вважати, що на систему керування впливає дія лише завдання Y(p) (збурення вважають відсутнім, f(p)=0), а вихідною величиною є координата стану об’єкта керування Х(р), тому, враховуючи характер з’єднань окремих складових системи, за відповідну функцію передачі слід прийняти:

	xy ( p)	X ( p)		Wкч( р) Wоб( p)	,	(1.33)
		Y ( p)		1 Wкч( р) Wоб ( p)

яку називають функцією передачі замкненої системи для керованої величини Х(р) по завданню Y(p). Добуток двох функцій передачі, що входить до означеного виразу являє собою еквівалентну функцію передачі W(p) послідовно з’єднаних керуючої частини і об’єкту керування, тобто розімкненої системи (без урахування від’ємного зворотного зв’язку):

W(p) = Wкч(p)·Wоб(p).

Виконавши відповідну підстановку, отримаємо у кінцевому вигляді:

	xy ( p)	X ( p)		W ( р)	.	(1.34)
		Y ( p)		1 W ( р)

Якщо вважати, що на систему керування, як і попередньому випадку, впливає дія лише завдання Y(p), але вихідною величиною є помилка керування ε(р), то відповідну функцію передачі для помилки керування по завданню y ( p)

визначити неважко:

y ( p)

( p)

Y ( p) - X ( p)

1-

X ( p)

1- xy ( p)

1-

W ( р)

1

.

(1.35)

Y ( p)

Y ( p)

1

W ( р)

1 W ( р)

Y ( p)

Для визначення функції передачі xf ( p)

для керованої величини Х(р) по

збуренню f(p) структурну схему треба дещо перетворити, виконуючі необхідні правила перетворення. В результаті перетворень схема набуває вигляду, який відображено на рис. 1.17

f(p)	Wзб(p)	1
		W ( p)		X(p)
Y(p)			ε(p)
				W(p)

Рис. 1.17

Приймаючі до уваги, що вхідною величиною будемо вважати збурюючий вплив f(p) (Y(p)=0), а вихідною координата стану об’єкта керування Х(р), відповідна функція передачі для керованої величини Х(р) по збуренню f(p) матиме вигляд:

	xf ( p)	X ( p)	Wзб ( р)		W ( р)		Wзб( р)	(1.36)
		f ( p)			1 W ( р)		1 W ( р)
			W ( р)

Порівнюючи всі три різновиди функцій слід звернути увагу на тотожність їх знаменників. Це дуже важлива особливість, тому що знаменник являє собою ліву частину рівняння динаміки системи керування. Тож, прирівнявши вираз знаменника до нуля, отримаємо характеристичне рівняння, яке характеризує особисті властивості системи не пов’язані з характером та місцем прикладення зовнішніх впливів. Отже, при вивченні особистих властивостей системи керування, наприклад, таких як стійкість, яким різновидом функції передачі не користуватися, отримаємо однаковий результат.

1.2.5 Статичні і динамічні і характеристики.

Рівняння статики відбиває в аналітичній формі зв'язок між вихідною й вхідною величинами в сталому режимі, яке можна отримати шляхом підстановки в рівняння динаміки значення р=0.

Графічне зображення залежності вихідної величини від вхідної в сталому режимі називається статичною характеристикою.

Перехідною функцією h(t) називається аналітичний опис зміни вихідної величини у часі при одиничній стрибкоподібній зміні вхідної величини при нульових початкових умовах. Перехідна функція відбиває реакцію елементу або системи в цілому на одиничний ступінчастий вплив при нульових початкових умовах, що по суті являє собою перехідний процес, який виникає в елементі при одиничному стрибку сигналу на вході 1(t) (хвх(t) = 0 при t 0; хвх(t) = 1 при t > 0).

Перехідна функція може бути отримана шляхом розв’язку диференціального рівняння класичним методом або, використовуючи перетворення Лапласа, операційним методом.

Для визначення зображення по Лапласу вихідної величини операційним методом в рівняння

Хвих(р) = W(p)Хвх(р)

(1.37)

замість Хвх(р) треба підставити зображення по Лапласу одиничного стрибка L

p та вираз функції передачі

W ( p)

1(t)

1

W(p)

bmpm bm-1pm-1 b0

.

(1.38)

a

n

pn a

pn-1

a

0

n-1

Оскільки за визначенням зображення по Лапласу перехідної функції H(p) і є зображення по Лапласу вихідної величини Хвх(р) при одиничному стрибку, то

H ( p) W ( p) .	(2.38)
p

Оригінал перехідної функції h(t) можна визначити по відповідним таблицям зворотного перетворення Лапласа або користуючись теоремою розкладення. В останньому випадку послідовність визначення полягає в наступному.

В загальному випадку, при відсутності нульових полюсів, H(p) має вигляд дробно-раціональної функції:

	H p	F1	p	,	(2.39)
		F2	p

де F1(p) - чисельник зображення по Лапласу перехідної функції H(p); F2 (p) - знаменник зображення по Лапласу перехідної функції H(p).

В такому випадку перехідну функцію h t можна визначити за основною формулою теореми розкладення:

F p

F p

1

n

1

k

h t L-1

epkt

,

(2.40)

1

F2 p

k 1 F2 pk

де n – степінь поліному F2 p ;

– корені характеристичного рівняння F

p

p 0 , k 1, n ;

k

2

F1

( p ) = dF2 ( p)

похідна

знаменника

зображення по

Лапласу перехідної

-

2

k

dp

p pk

функції H(p).

В випадку однократного нульового полюса зображення за Лапласом

перехідної функції має вигляд дробу:

H p

F1 p

.

(2.41)

pF2 p

Оригінал перехідної функції h t можна визначити за додатковою

формулою теореми розкладення:

0

F

p

F p F

1

n

1

k

h t

L-1

1

epkt

(2.42)

F2

0

1

pk

pF2 p

k 1 pk F2

Перехідна характеристика є графічним відображенням перехідної функції h(t) , являючи собою графічне зображення зміни вихідної величини у часі при одиничній стрибкоподібній зміні вхідної величини.

Окрім перехідної характеристики існує ще імпульсна характеристика. Вона являє собою реакцію елементу або системи керування в цілому на вхідний імпульс необмеженої величини при нульовій його тривалості (δ-функція). Теоретично δ-функція дорівнює похідній одиничного стрибка

δ(t)= d1(t) ,		(2.43)
	dt
а площа імпульсу S дорівнює одиниці, тобто:
		(2.44)
S =	(t)dt 1.
0

Аналітичний вираз, по якому будується імпульсна називається функцією ваги w(t). Між функцією ваги w(t) характеристикою h(t) існує однозначний взаємозв’язок:

w (t ) dh (t ) , dt

характеристика, і перехідною

(2.45)

а функція передачі W(p) являє собою пряме перетворення Лапласа функції ваги w(t)

W ( p)	w(t)e- ptdt .	(2.46)
	0
1.2.6 Частотні характеристики.
Для оцінки частотних	властивостей елементів і	систем широко

використовуються так звані частотні характеристики.

Розглянемо систему керування, рівняння динаміки якої записано в

операторній формі:
аnрnхвих(t)+ аn-1рn-1хвих(t)+…….+ а0хвих(t) =	(2.47)
=bmpmxвх(t)+ bm-1pm-1xвх(t)+…….+ b0xвх(t).
Нехай на вхід системи поданий гармонічний сигнал
хвх(t) = Авх Sin ωt.	(2.48)
Після закінчення перехідного процесу на виході	системи керування

встановляться теж гармонічні коливання з тією ж частотою, але з іншою амплітудою і зсунуті по фазі на кут φ відносно вхідного впливу:

хвих(t) = Авих sin (ωt+φ(ω)),

(2.49)

де Авх, Авих – амплітуди вхідного та вихідного сигналів відповідно; φ(ω) – кут зсуву по фазі вихідного сигналу, який залежить від частоти вхідного сигналу.

Використаємо комплексну форму запису:

хвх(t) = Авх ejωt;

(2.50)

хвих(t) = Авих e(jωt+φ(ω)).

Підставимо ці значення в операторну форму диференціального рівняння,

враховуючі

при

цьому,

що еj(ωt+φ(ω)) = еjωt

еjφ(ω);

рк(Авхеjωt)

= (jω)кАвхеjωt;

рк(Авихеj(ωt+φ(ω))) = (jω)кАвихеjωt еjφ(ω):

(аn(jω)n+ аn-1(jω)n-1+…….+ а0) Авихеjωt еjφ(ω) =

(2.51)

звідки:

= (bm(jω)m+ bm-1(jω)m-1+…….+ b0) Авхеjωt

A

b ( j )m b

( j )m-1 ......b ( j ) b

B( j )

W ( j )

вих

e j ( )

m

m-1

1

0

.

an ( j )n an-1(

A( j )

(2.52)

Aвх

j )n-1 ...... a1( j ) a0

P( ) jQ( )

де P(ω) – дійсна частина;

Q(ω) – уявна частина.

Неважко побачити, що ліва частина рівняння являє собою функцію передачі, в якій зроблена підстановка р = jω. Оскільки ця величина являє собою комплексне число, то її можна записати у вигляді:

Вираз W(jω) називають комплексним коефіцієнтом передачі, або комплексною функцією передачі. Як кожну комплексну величину, її можна

	представити або в декартовій, або полярній системі координат.
		W(jω) = P(ω) + jQ(ω),								(2.53)
	або:
		W(jω) = A( )e j ( ) ,								(2.54)
	де А(ω) – коефіцієнт передачі системи на частоті ω, є модулем									комплексного
	коефіцієнту передачі W(jω):
	А(ω) =	Aвих	=		W(jω)		= P2 ( ) Q2 ( ) ,			(2.55)
		Aвх
	φ(ω) – зсув по фазі вихідного сигналу, є аргументом комплексного
	коефіцієнту передачі W(jω) на тій же частоті ω:
	φ(ω) = arg(W(jω)) = arc tg							Q( )	.	(2.56)
								P( )

Графічне відображення комплексного коефіцієнту передачі А(ω) в комплексній площині називають амплітудно-фазовою частотною характеристикою:

Графічне зображення залежності коефіцієнта передачі А(ω) від частоти називається амплітудно-частотною характеристико (АЧХ) , а залежності зсуву по фазі φ(ω) вихідного сигналу від частоти – фазово-частотною характеристикою (ФЧХ).

А(ω)	φ(ω)

0 ω

0 ω

Обидві частотні характеристики можна побудувати в логарифмічних координатах. При побудові логарифмічної амплітудно-частотної характеристики (ЛАЧХ) по осі абсцис відкладають логарифм частоти в декадах, а по осі ординат L(ω)= 20 lg A(ω) в децибелах. Для логарифмічної фазово-частотної характеристики (ЛФЧХ) по осі ординат відкладають значення фази в радіанах або в градусах.

Під декадою розуміють масштабний відрізок на осі абсцис, співвідношення частот на кінцях якого дорівнює 10.

L(ω), дВ		φ(ω), рад

	lgω, дек
		0
0

В теорії автоматичного керування іноді використовують побудову залежностей дійсної P(ω), а також уявної Q(ω) частин комплексного коефіцієнту передачі від частоти, отримуючи таким чином дійсну частотну та уявну частотну характеристики ДЧХ і УЧХ. ДЧХ в свій час була дуже поширена, оскільки являлася основою для побудови перехідних характеристик систем керування завдяки однозначному її зв’язку з перехідними процесами. З розвитком сучасних засобів обчислювальної техніки та числових методів рішення диференціальних рівнянь використання ДЧХ дещо зменшилося.

1.3 Типові динамічні ланки.

Типовою динамічною ланкою називається частина системи автоматичного керування, яка описується лінійним диференціальним рівнянням не вище другого порядку.

Для типової динамічної ланки другого порядку рівняння динаміки в загальному випадку в операторній формі запису має вигляд:

a2 p2 a1p a0 xвих t b2 p2 b1p b0 xвх t ,

(3.1)

Функція передачі ланки другого порядку:

де p – оператор диференціювання, p dtd ;

xвх t – сигнал на вході ланки; xвих t – сигнал на виході ланки;

a2 , a1 , a0 , b2 b1 b0 – сталі коефіцієнти.

Зображення за Лапласом лінійного диференціального операційній формі (при нульових початкових умовах) має вигляд:

a2 p2 Xвих p a1pXвих p a0 Xвих p b2 p2 Xвх p b1pXвх p b0 Xвх p

або

a2p2 a1p a0 Xвих p b2 p2 b1p b0 Xвх p ,

де p – оператор Лапласа;

Xвх p – зображення за Лапласом сигналу на вході ланки; Xвих p – зображення за Лапласом сигналу на виході ланки.

W p	Xвих p				b2 p2	b1p b0			.
	X	вх	p		a p2	a p a
					2	1	0

рівняння в

(3.2)

(3.3)

(3.4)

Як правило, рівняння динаміки в операційній формі прийнято приводити до нормованого вигляду:

a2

p2

a1

p 1 X

вих

p b0

b2

p2

b1

p 1 X

вх

p

a0

a0

b0

a0

b0

або

p K T T p2

p ,

TT p2

T p 1 X

вих

T p 1 X

вх

1

2

2

3 4

4

де K – сталий коефіцієнт (коефіцієнт передачі):

K b0 ; a0

T1, T2 , T3 , T4 – сталі коефіцієнти:

T a2		, T	a1	, T b2		, T	b1	.
1	a1	2	a0	3	b1	4	b0

Розмірність коефіцієнта K залежить від розмірностей сигналів

(3.5)

(3.6)

(3.7)

(3.8)

xвх t і xвих t

. При однакових розмірностях сигналів xвх t і

xвих t коефіцієнт K є

безрозмірним, а інші коефіцієнти T1, T2 , T3 , T4 мають розмірність часу.

Лінійним динамічним ланкам прийнято давати назви в залежності від виду лівої і правої частин рівнянь динаміки.

Для наведених нижче ланок ліва частина рівняння динаміки має наступний вигляд:

- ідеальна ланка (T1 0 , T2 0 ):

	Xвих p ;								(3.9)
- аперіодична ланка першого порядку (T1 0 , T2 T ):
Tp 1 Xвих p ;									(3.10)
- аперіодична ланка другого порядку (T						T	,	T 2dT , d 1):
			1			2d		2
T 2 p2 2dTp 1 Xвих p ;									(3.11)
- коливальна ланка (T		T	, T 2dT ,	0 d 1):
1		2d	2
T 2 p2 2dTp 1 Xвих p ,									(3.12)

де d показник (декремент) затухання.

З наведеного випливає, що останні дві ланки (аперіодична та коливальна) є ланками другого порядку і мають однакові на вигляд рівняння динаміки, а отже однакові на вигляд функції передачі. Різницю ланок обумовлює числове значення декременту затухання d.

Якщо d≥1, то корені характеристичного рівняння будуть дійсними, в перехідному процесі такої ланки відсутня коливальна складова, перехідний процес має монотонний характер. Така типова динамічна ланка називається аперіодичною (інерційною) ланкою другого порядку.

Якщо 0<d<1, то корені характеристичного рівняння будуть комплексними спряженими, в такому випадку перехідний процес матиме коливальний характер.

Така типова динамічна ланка має назву коливальної.	T 0	і d 0, є
Обидві розглянуті ланки, якщо виконуються умови
стійкими тому, що в усталеному (статичному) режимі вихідний сигнал xвих t
наближається до певного постійного значення. При T <0	абоd<0	усталений

режим неможливий, вихідний сигнал ланки буде коливатися з безперервно

зростаючою до нескінченності амплітудою (нестійка ланка),	а при d 0
амплітуда коливань стає постійною (ланка на межі стійкості).
Для наведених нижче ланок права частина рівняння динаміки має
наступний вигляд:
- проста ланка:
KXвх p ;	(3.13)
- диференціююча ланка:
KpXвх p ;	(3.14)
- інтегруюча ланка:
K Xвх p ;	(3.15)
p

- ланка з введенням похідної: