1.3. Упруго-пластическая задача

Система уравнений, описывающих процесс упруго-пластической деформации,состоит из уравнений равновесия, совместности деформа­ций, реологического уравнения и условия пластичности, например, условия пластичности Мизеса:

Где — квадратичный инвариант девиатора напряжений; σ_т — предел текучести при одноосном растяжении.

Рассмотрим два тела, одно из которых — металл, испытываю­щий упруго-пластическую деформацию под действием известных внешних сил, а второе — фотопластичная модель из высокополимера, на которой изучается напряженно-деформированное состояние первого тела .

Для обеспечения подобия полей напряжений в модели и натуре необходимо, чтобы одно поле из другого могло быть получено путем умножения компонентов первого поля на скалярный множитель т, т. е.

(20)

здесь тензор напряжения в точках натуры;

— то же, в точках модели.

Условия подобия, которым должны удовлетворять внешние силы без учета инерционных сил, записываются как

где —составляющие вектора плотности поверхностных сил для натуры и модели соответственно.

На границе деформируемого тела — натуры могут быть заданы не только силы, но и перемещения. В этом случае определенным условиям должны удовлетворять и перемещения на соответствующей части модели. Однако точно сформулировать эти условия можно лишь располагая реологическими уравнениями обоих тел. Из этих уравнений будут вытекать дополнительные условия подобия, кото­рым должны удовлетворять свойства материалов натуры и модели с тем, чтобы было возможно подобие полей согласно уравнению (20).

Можно показать, что в случае моделирования упруго-пластиче­ской задачи на высокополимерах из условия подобия полей напря­жений (20) вытекает требование подобия полей деформации

(21)

Коэффициент подобия С' в этом случае составит

где — модули объемного расширения для модели и натуры соответственно.

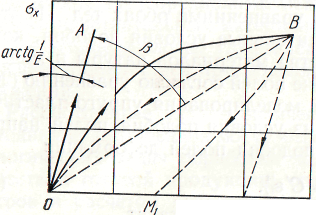
Сравним диаграммы растяжения образцов из высокополимера и металла. При достаточно быстром нагружении полимерного об­разца деформация происходит лишь за счет изменения расстояния между каждой парой атомов (узлов цепи), т. е. за счет тех же при­чин, что и упругая деформация обычных твердых тел (в частности, металлов). Связь напряжений с деформациями при таком нагруже­нии описывается законом Гука (линия О А на рис. 2, а). Если прило­женную силу поддерживать неизменной, то в полимерном теле будет развиваться во времени высокоэластическая деформация, прибли­жаясь со все убывающей скоростью к своему равновесному зна­чению, т. е. высокоэластическая деформация будет развиваться как деформация ползучести при постоянной нагрузке. Если же осущест­влять нагружение весьма медленно, так, чтобы средневременные конформации цепей в каждый момент процесса соответствовали те­кущей величине макроскопических напряжений, то такое нагруже­ние носит название термодинамически равновесного и ему соответст­вует кривая ОБ. К этой кривой близка кривая ВО (показана пункти­ром) термодинамически равновесной разгрузки, которая получается при достаточно медленном разгружении. При быстрой (мгновенной) разгрузке полимерного образца процесс разгрузки происходит по прямой ВМ, параллельной О А, а при «промежуточных» скоростях — по кривым типа ВМ_г. Таким образом, в первый момент после бы­строй разгрузки образец имеет некоторую остаточную деформацию, которая постепенно (иногда весьма медленно) убывает за счет теп­лового движения молекул.

Процессы термодинамически равновесного нагружения и пол­зучести при постоянной нагрузке являются основными при моде­лировании упруго-пластических задач. Каждый из названных про цессов имеет свои особенности, определяющие в значительной мере методику моделирования, поэтому рассмотрим их отдельно.

1. В случае термодинамически равновесного нагружения моде­ли, к которому при достаточно высокой температуре близок реаль­ный процесс высокоэластической деформации полимера, реологи­ческое уравнение имеет следующий вид:

(22)

где — функция второго инварианта девиатора на­пряжений. Значение этой функции может быть получено из диа­граммы растяжения (рис. 2,а), оно пропорционально тангенсу угла Характерной особенностью реологического поведения ме­таллов, по сравнению с полимерами, является почти полное отсутст­вие эффекта последействия, т. е. неизменность остаточных деформаций, вследствие чего остаточная деформация равна пластической. При этом основным механизмом пластической деформации являются необ­ратимые сдвиги (скольжение) в кристаллитах поликристалла. Бла­годаря сдвиговой природе пластической деформации можно с достаточной степенью точности считать, что тензор пластической дефор­мации представляет собой девиатор. Далее, возможно положить, что девиаторыи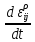соосны и подобны, т.е.

,

где А — некоторая скалярная величина, меняющаяся от точки к точке.

Если ограничиться случаем простого монотонного нагружения и малых деформаций, то здесь соосность и подобие будут иметь место также между тензором пластической деформации и девиатором напряжений:

Функция Ф (l₂) может быть найдена из опытов на одноосное рас­тяжение или чистый сдвиг. На диаграмме растяжения (рис. 2, б), построенной в координатах σ_х, ε_х, функция Ф пропорциональна значению тангенса угла β:

где Е = 2G (1 + μ) — модуль упругости при растяжении.

2. Экспериментальные исследования ползучести полимерных материалов показывают, что при постоянных напряжении и темпера­туре поведение полимерных материалов описывается теми же урав­нениями, что и поведение металлов и сплавов :

(23)

Здесь — полная деформация;— упругая деформация;

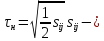интенсивность касательных напряжений.

Распределение напряжений в конкретной задаче существенно зависит от формы функций φ(t) и f(τ_и) которые находят путем обра­ботки экспериментальных кривых ползучести. Важное значение для моделирования ползучести имеет также то обстоятельство, что для полимерных материалов функции φ(t) и f(τ_и) можно аппроксими­ровать такими же зависимостями, как и для металлов.

На полимерных материалах можно моделировать поля напряже­ний в металлах и сплавах в условиях установившейся и неустановив­шейся ползучести. Известно, что в металлах при неоднородном поле напряжений может быть достигнуто состояние установившейся пол­зучести, в котором напряжения и скорости деформации стационарны. Поскольку кривые ползучести некоторых полимерных материа­лов так же как и кривые ползучести металлов геометрически подобны и полные деформации ползучести сравнительно быстро нарастают, достигая величин порядка упругих деформаций, то в полимерных моделях достижимо состояние квазиустановившейся ползучести, при котором поле напряжений стационарно, а поле деформаций ползучести — переменно. Такое состояние реализуется при посто­янных внешних нагрузках и температуре.

Уравнения ползучести в этом случае отличаются от уравнения (23) тем, что в них не учитывается упругая деформация:

(24)

Функция φ(t), входящая в уравнение квазиустановившейся ползучести (24), нелинейна, в то время как для состояния установившейся ползучести φ(t), и—линейна. Поскольку φ не входит систему уравнений в напряжениях, поля напряжений в состояниям установившейся и неустановившейся ползучести при рассматриваемых граничных условиях одинаковы.

Для моделирования установившейся ползучести металлов могу! применяться изотропные полимерные материалы, находящиеся I стеклообразном и переходном состояниях. При комнатной темпера­туре — это полистирол, целлулоид, плексиглас, полиэфирные смоль и др. В таких состояниях полимерные материалы проявляют суще­ственную ползучесть при малых деформациях.

На этих же полимерных материалах можно моделировать и состояние неустановившейся ползучести. В таком состоянии поле напряжений изменяется монотонно с убывающей скоростью. При этом для перенесения результатов испытаний с модели на натуру можно использовать в качестве закона ползучести уравнение (23). Связь между напряжениями в модели и натуре в сходственные моменты времени определяется соотношениями

где— внешние нагрузки в модели и натуре соответственно. Сходственные моменты времени находятся графически из усло­вия

(25)

где Е — модуль упругости.

Из выражения (25) следует, что функция φ(t), может иметь раз­личную форму для материалов модели и натуры. Это обстоятельство облегчает выбор материала моделей. Тот факт, что при ползучести металлов накапливается в основном необратимая деформация, а при ползучести полимеров — в основном обратимая деформация, не имеет значения.

Коэффициент Пуассона, входящий в уравнение (23), не является существенным критерием подобия, поэтому небольшим различием коэффициентов Пуассона для модели и натуры можно пренебречь. При выборе материала модели необходимо учитывать его пьезо-оптические свойства . Для неупругих сред оптическая разность хода связана не только с разностью главных напряжений, но и с разностью главных деформаций, уравнением Файлона — Джессопа:

Следует отметить, что в том и другом случае оптическая разность хода обусловлена оптической анизотропией, возникающей в поли­мерном теле во время деформации. Однако природа двойного луче­преломления, вызванного упругой деформацией, коренным обра­зом отличается от природы оптического эффекта, полученного в ре­зультате высокоэластической деформации. Это различие отмечается в уравнении (26) разделением правой части на два слагаемых, пер­вое из которых описывает атомарный эффект, а второе — сегменталь­ный. Величину и знак коэффициентов С_σ и С_ε уравнения (26) на­ходят экспериментально. Полосы интерференционной картины при δ=const определяют геометрическое место точек, для которых

т. е. каждая полоса определяет некоторое сочетание величин (()

Для того, чтобы выразить ∆ только через одну из названных раз­ностей, нужно использовать закон деформации рассматриваемой среды. С этой целью для среды, проявляющей ползучесть, может быть использовано уравнение (26), которое после приведения к глав­ным осям с учетом того, чтоможет быть пред­ставлено в следующем виде:

(27)

Подставляя выражение (26) в уравнение (27) и заменяя τ_и что допустимо при малых деформациях, записываем

Из полученной зависимости следует, что в этом случае изохромы при δ = const будут представлять собой линии посто­янных значений разности. Построив зависимостьдля различныхt получим семейство изохронных ли­ний, которые можно использовать для перехода от измеренных зна­чений ∆ к разности (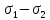). Изохронные кривые строят по ре­зультатам измерения ∆ в испытаниях на одноосное растяжение или сжатие при постоянных нагрузках и температуре. Таким образом, в рассматриваемом методе фотоползучести переход от ∆ к()осуществляется в отличие от метода фотоупругости не с помощью уравнения Вертгейма (11), а по экспериментально найденным изо­хронным кривым.

Описанная методика перехода от ∆ к напряжениям использо­валась при моделировании процесса ползучести на моделях из полистирола. Применение такой методики позволяло в случае одно­осного неизменного напряженного состояния получать точные значения (), а в случае сложного напряженного состояния и пе­ременных напряжений — приближенные значения.

Располагая значениями разности () и параметров изо­клин, определяют компоненты напряжений путем интегрирования дифференциальных уравнений равновесия, наклонного просвечи­вания и других принятых в фотоупругости методов, в которых не используется закон Гука и поэтому пригодных для неупругих мо­делей.