
02_Metodichka_MMSA
.docМатематичною
моделлю процесу зміни величини доходу
фірми є функція
![]() ,
яка, у свою чергу, є розв’язком задачі
Коші:
,
яка, у свою чергу, є розв’язком задачі
Коші:
![]() .
.
Одержане рівняння є лінійним диференціальним рівнянням першого порядку зі сталими коефіцієнтами. Його розв’язок має такий вигляд:
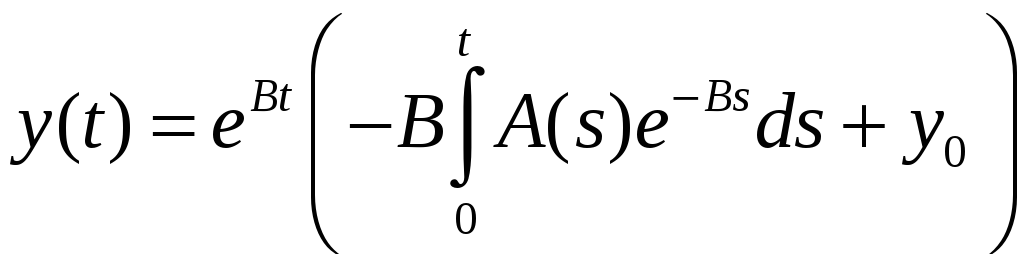 .
.
Ця
функція дозволяє дослідити поведінку
величини доходу
![]() при різних законах зміни споживання
при різних законах зміни споживання
![]() .
.
Побудована модель економічного процесу є детермінованою дескриптивною моделлю з неперервним часом. У цій моделі неперервність часу обумовлена тим, що реально фінансові показники фірми змінюються з плином часу, як правило, неперервно.
Тема 5. Оптимізаційні моделі
Студентам спеціальності “Прикладна математика” викладається об’ємний та змістовний курс “Методи оптимізації”, який цілком присвячений вивченню оптимізаційних моделей. Щоб запобігти дублюванню, в нашому курсі розглядаються моделі оптимізації руху та моделі оптимізації споживання.
Моделі Стоуна, Торнквіста, Эджворта [3, гл.9] демонструють застосування математичного апарату, пов’язаного з методами пошуку оптимальних значень змінних, дозволяють вивчати закони функціонування реальних економічних систем.
5.1. Задача споживчого вибору
Постановка задачі. Споживач має змогу витратити на споживання певного асортименту товарів та послуг суму I – споживчий бюджет. Асортимент складається з n видів товарів та послуг. Вважається заданою функція корисності споживчого набору, що вказує, яку користь матиме споживач від споживання певної кількості означених товарів та послуг. Необхідно з’ясувати, яку кількість кожного товару чи послуги повинен спожити споживач, щоб мати найбільшу користь і при цьому не вийти за межі визначеного споживчого бюджету.
Перш ніж розв’язувати цю
задачу, необхідно попередньо її
формалізувати. Позначимо через
![]() ,
кількість i-го
товару, що споживач вирішив придбати.
Тоді вектор
,
кількість i-го
товару, що споживач вирішив придбати.
Тоді вектор
![]() є споживчим набором споживача. Припустимо,
що нам відома функція
є споживчим набором споживача. Припустимо,
що нам відома функція
![]() ,
яка вказує, яку користь матиме споживач
від споживання набору
,
яка вказує, яку користь матиме споживач
від споживання набору
![]() .
Від цієї функції вимагатимемо виконання
наступних умов (далі для спрощення
записів вважатимемо, що п=2).
.
Від цієї функції вимагатимемо виконання
наступних умов (далі для спрощення
записів вважатимемо, що п=2).
-
Функція визначена для будь-яких
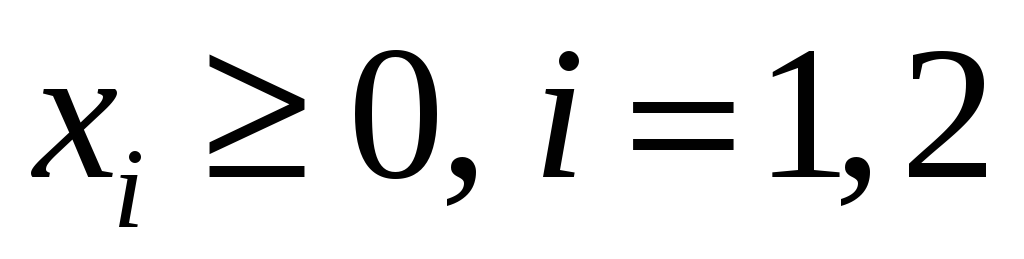 .
. -
Функція набуває невід’ємних значень.
-
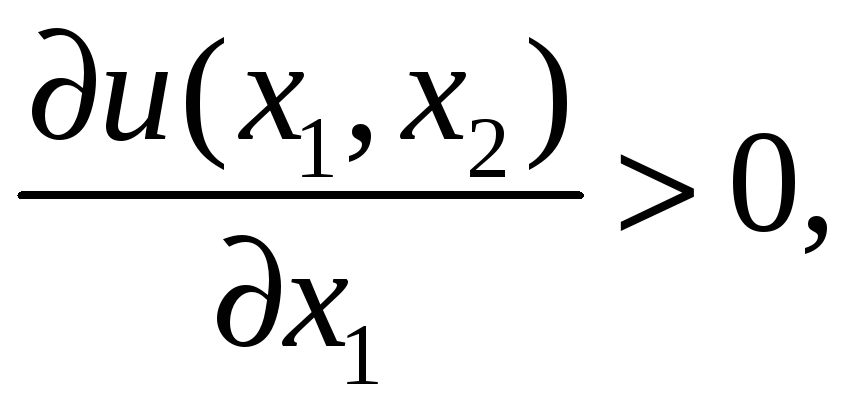
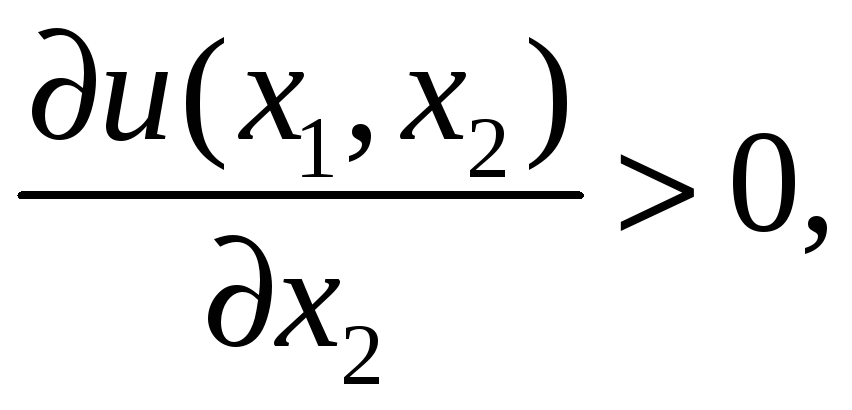 тобто зростання обсягів
споживання одного товару при незмінних
обсягах споживання іншого товару веде
до зростання корисності.
тобто зростання обсягів
споживання одного товару при незмінних
обсягах споживання іншого товару веде
до зростання корисності. -
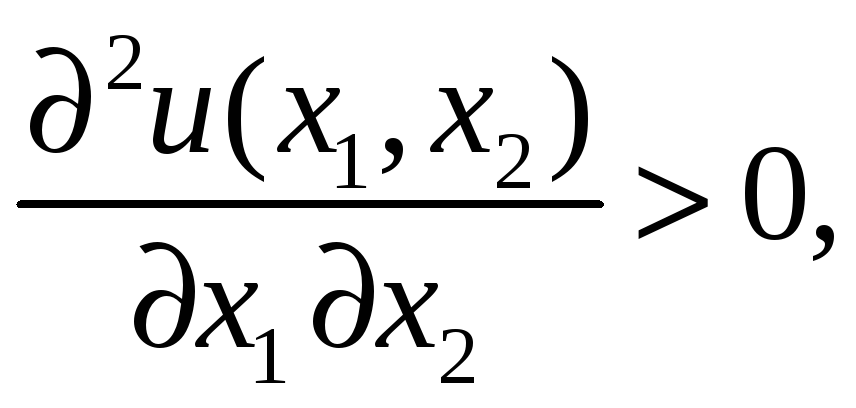 тобто гранична корисність кожного
товару зростає, якщо збільшується
обсяг споживання іншого товару.
тобто гранична корисність кожного
товару зростає, якщо збільшується
обсяг споживання іншого товару. -

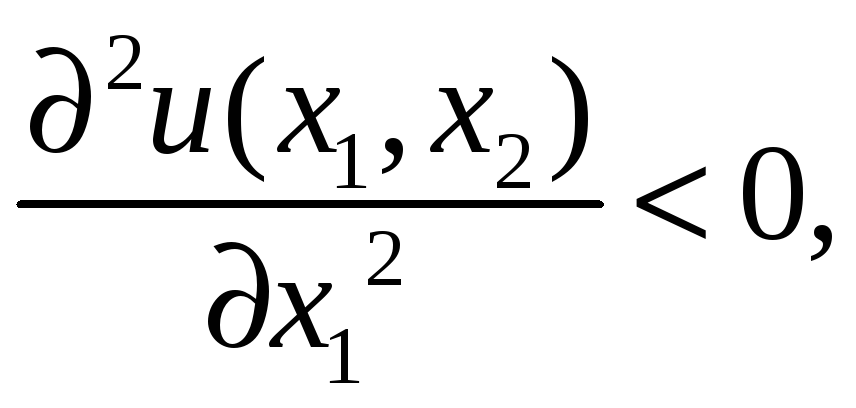 тобто гранична корисність
товару зменшується, якщо збільшується
обсяг його споживання.
тобто гранична корисність
товару зменшується, якщо збільшується
обсяг його споживання.
Будемо позначати
![]() ціну за одиницю i-го
товару зі споживчого набору. Тепер із
точки зору математичної постановки
проблеми задача споживчого вибору має
такий вигляд.
ціну за одиницю i-го
товару зі споживчого набору. Тепер із
точки зору математичної постановки
проблеми задача споживчого вибору має
такий вигляд.
На множині неві’ємних
розв’язків нерівності
![]() необхідно знайти точку, в якій функція
необхідно знайти точку, в якій функція
![]() досягає свого найбільшого значення.
досягає свого найбільшого значення.
Зауваження.
Сформульована задача є коректною,
оскільки множина
![]() є обмеженою та замкненою, а функція
є обмеженою та замкненою, а функція
![]() неперевна на цій множині.
неперевна на цій множині.
Сформульовану задачу можна
спростити, оскільки можна довести, що
її оптимальний розв’язок задовольняє
рівність
![]() .
Тоді означена задача стає задачею на
умовний екстремум і може бути розв’язана,
наприклад, за допомогою функції Лагранжа.
.
Тоді означена задача стає задачею на
умовний екстремум і може бути розв’язана,
наприклад, за допомогою функції Лагранжа.
Приклад 5.1.
Розглянемо модель
Стоуна. В ній функція
корисності має такий вигляд:
![]() .
Числа
.
Числа
![]() і
і
![]() є невід’ємними і вказують на мінімально
небхідні обсяги споживання товарів.
Числа
є невід’ємними і вказують на мінімально
небхідні обсяги споживання товарів.
Числа
![]() і
і
![]() є додатними і
є додатними і
![]() .
Вони вказують на значущість того чи
іншого товару в споживчому наборі.
.
Вони вказують на значущість того чи
іншого товару в споживчому наборі.
Зазначимо, що наведена функція
Стоуна задовольняє умови 1 – 5. Функція
Стоуна досягає найбільшого значення
на множині припустимих наборів у точці
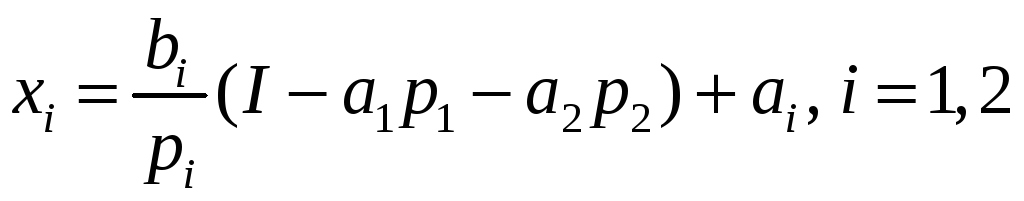 .
Аналіз отриманої формули вказує, що
споживач повинен спочатку придбати
мінімальну кількість
.
Аналіз отриманої формули вказує, що
споживач повинен спочатку придбати
мінімальну кількість
![]() кожного товару, а залишок коштів
розподілити пропорційно до відношення
значущості товару до його ціни.
Відзначимо, що одержана функція є
дробово-лінійною функцією від цін на
товари. Це відповідає реально існуючим
взаємозв’язкам між цінами та обсягами
споживання. Однак ця модель є скоріш
теоретичною й описує лише принциповий
характер зв’язків. Більш наближеною
до дійсності є, наприклад, модель
Торнквіста.
кожного товару, а залишок коштів
розподілити пропорційно до відношення
значущості товару до його ціни.
Відзначимо, що одержана функція є
дробово-лінійною функцією від цін на
товари. Це відповідає реально існуючим
взаємозв’язкам між цінами та обсягами
споживання. Однак ця модель є скоріш
теоретичною й описує лише принциповий
характер зв’язків. Більш наближеною
до дійсності є, наприклад, модель
Торнквіста.
Побудована модель дозволяє вивчати можливі наслідки тих чи інших економічних явищ.
Приклад
5.2. Розглянемо задачу
компенсації споживчого бюджету
при зростанні ціни на товар для моделі
Стоуна. Припустимо, що ціна на перший
товар зросла у k
разів, а на другий залишилась незмінною.
З’ясуємо, як треба змінити споживчий
бюджет I,
щоб рівень споживання не змінився.
Нехай
![]() і
і
![]() – початкові ціни на товари, а І
– початковий споживчий
бюджет. Тоді після зростання ціни
першого товару в k
разів при незмінній ціні на другий
товар та початковому бюджеті оптимальний
обсяг споживання дорівнюватиме:
– початкові ціни на товари, а І
– початковий споживчий
бюджет. Тоді після зростання ціни
першого товару в k
разів при незмінній ціні на другий
товар та початковому бюджеті оптимальний
обсяг споживання дорівнюватиме:
 ,
,
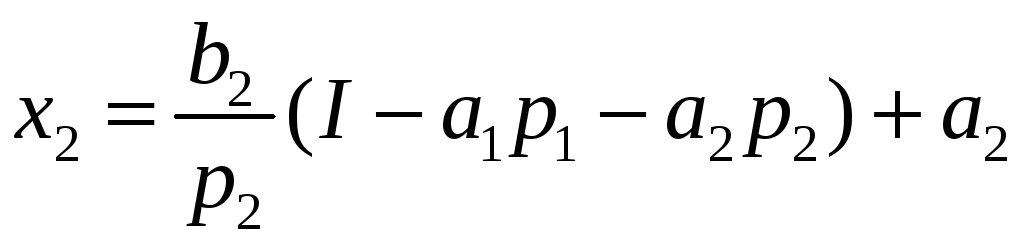 .
.
Збільшимо
споживчий бюджет на величину
![]() .
Тоді новий оптимальний обсяг споживання
дорівнюватиме:
.
Тоді новий оптимальний обсяг споживання
дорівнюватиме:
 ,
,
 .
.
Доберемо
![]() таким, щоб рівень корисності після
зростання ціни та збільшення бюджету
був таким, як початковий.
таким, щоб рівень корисності після
зростання ціни та збільшення бюджету
був таким, як початковий.
![]() .
.
Число
![]() називають індексом
компенсації споживчого бюджету.
Він указує, у скільки разів треба
збільшити споживчий бюджет, щоб
компенсувати зростання цін на товари.
називають індексом
компенсації споживчого бюджету.
Він указує, у скільки разів треба
збільшити споживчий бюджет, щоб
компенсувати зростання цін на товари.
Якщо
підставити розмір компенсації
![]() у новий оптимальний споживчий набір,
то отримаємо:
у новий оптимальний споживчий набір,
то отримаємо:
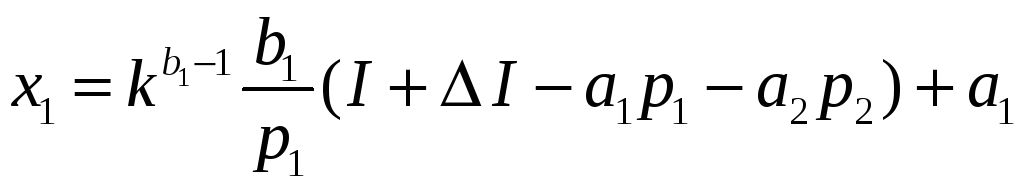 ,
,
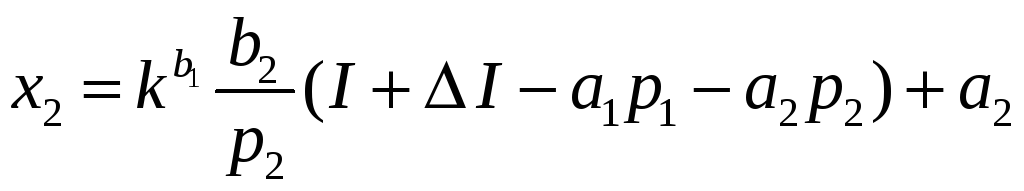 .
.
Оскільки
![]() і
і
![]() ,
то ми бачимо, що зростання ціни на перший
товар та подальша компенсація бюджету
хоч і відновили початковий рівень
споживання, але змінили структуру
оптимального споживчого набору:
кількість споживання першого товару
зменшилась, а другого – зросла.
,
то ми бачимо, що зростання ціни на перший
товар та подальша компенсація бюджету
хоч і відновили початковий рівень
споживання, але змінили структуру
оптимального споживчого набору:
кількість споживання першого товару
зменшилась, а другого – зросла.
5.2. Задачі оптимізації руху
Задачі оптимізації руху розглянемо на прикладі одного з варіантів задачі про маневрування автомобіля. Ключовою теоремою в цьому розділі є теорема Креггса.
Теорема 5.1. Нехай на площині є області, в які заборонено заходити. Найкоротший шлях між двома точками на площині або є відрізком прямої, або складається з частин меж заборонених областей та дотичних до цих меж.
Постановка задачі. На площині зафіксовані дві точки А і В, відстань між якими дорівнює d. У точці А, під прямим кутом до відрізка АВ, стоїть автомобіль, який необхідно перепаркувати в точку В також під прямим кутом до АВ і спрямувати автомобіль у той же бік, що і в точці А. Автомобіль має як передній, так і задній хід, але може здійснювати повороти не крутіші за коло радіуса r. Необхідно знайти найкоротший маршрут перепарковки автомобіля.
Розв’язок задачі залежить
від співвідношення між параметрами r
i d. Тому
розглянемо такі випадки: 1) ![]() ,
2)
,
2) ![]() ,
3)
,
3) ![]() .
Скористаємось теоремою Креггса.
Маршрути, які задовольняють умови
теореми Креггса, будемо називати
маршрутами Креггса.
.
Скористаємось теоремою Креггса.
Маршрути, які задовольняють умови
теореми Креггса, будемо називати
маршрутами Креггса.
Н ехай
ехай
![]() .
.
Рис.1
Згідно з умовами задачі, яким
би маршрутом не рухався автомобіль, у
будь-якій точці його траєкторії біля
авто виникають дві області, в які він
не може в’їхати. Це кола радіуса r,
які розташовані ліворуч
та праворуч від нього. Коли авто стоїть
у точці А,
одним із таких кіл є коло з центром
![]() .
Аналогічно, у точці В
виникає заборонене коло з центром
.
Аналогічно, у точці В
виникає заборонене коло з центром
![]() .
Таким чином, найкоротший шлях має
пролягати по межах цих кіл або дотичних
до них. Проведемо NQ
– спільну дотичну до кіл
.
Таким чином, найкоротший шлях має
пролягати по межах цих кіл або дотичних
до них. Проведемо NQ
– спільну дотичну до кіл
![]() і
і
![]() і розглянемо маршрут ANQB
(рис. 1).
Він є маршрутом Креггса,
і його довжина дорівнює
і розглянемо маршрут ANQB
(рис. 1).
Він є маршрутом Креггса,
і його довжина дорівнює
![]() .
.
Але це не єдиний маршрут Креггса. Побудуємо ще один (рис. 2).
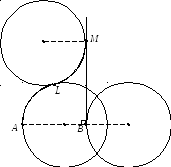
Рис.2
З
точки В
проведемо перпендикуляр до АВ
і побудуємо коло радіуса r
з центром
![]() ,
яке дотикається цього перпендикуляра,
та коло
,
яке дотикається цього перпендикуляра,
та коло
![]() .
Маршрут ALMB
є маршрутом Креггса, і його довжина
дорівнює
.
Маршрут ALMB
є маршрутом Креггса, і його довжина
дорівнює
![]() ,
де
,
де
![]() .
.
Окрім цих двох маршрутів розглянемо ще один маршрут Креггса (рис. 3), до складу якого не входять дотичні.

Рис.3
Це
маршрут ACDB,
у якому коло
![]() має радіус r
і дотикається кіл
має радіус r
і дотикається кіл
![]() і
і
![]() .
Довжина маршрута дорівнює
.
Довжина маршрута дорівнює
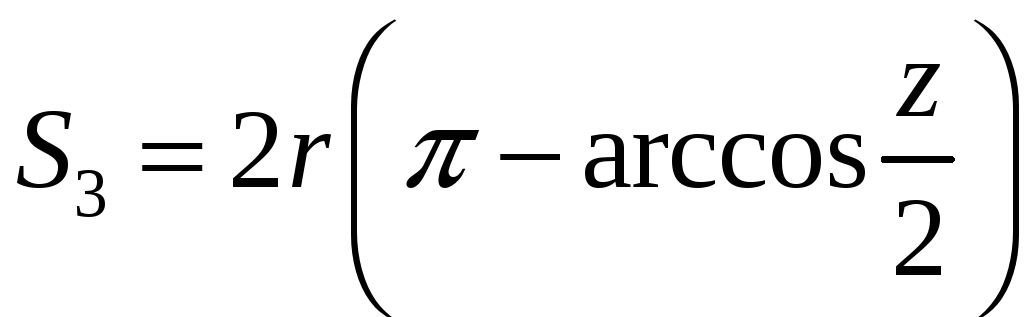 .
.
Є також інші маршрути Креггса, але вони або заздалегідь не коротші за наведені маршрути, або подібні до них. Розглядати маршрути, які не є маршрутами Креггса, взагалі немає сенсу згідно з теоремою.
Методами
математичного аналізу нескладно
з’ясувати, що у випадку
![]() найкоротшим є другий маршрут ALMB,
а у випадку
найкоротшим є другий маршрут ALMB,
а у випадку
![]() найкоротшим
стає маршрут ACDB.
найкоротшим
стає маршрут ACDB.
Н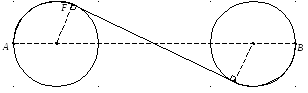 ехай
ехай
![]() .
.
Рис.4
Тепер
маршрути ALMB та
ACDB
стають неможливими. Але замість них
виникає новий варіант AFGB
(рис. 4), довжина якого
дорівнює
 .
В цьому випадку маршрут AFGB
коротший за маршрут
ANQB.
.
В цьому випадку маршрут AFGB
коротший за маршрут
ANQB.
Тема 6. Ігрові моделі
Ігрові моделі охоплюють значні галузі людської діяльності. Ігри у воєнній галузі, економічні ігри в конкурентній боротьбі, теорія конфліктів та компромісів, фінансові ігри – далеко не повний перелік галузей застосування ігрових моделей. З конкретними прикладами та типовими моделями слід ознайомитись в [1, гл.14], [3, гл.13],. Ключовим теоретичним фактом тут є теорема Неймана. Для її закріплення слід ретельно опрацювати приклади з §13.5, 13.7 [3], §6.4 [10].
Ігрові моделі класифікують за такими ознаками: кількість учасників, кількість можливих варіантів поведінки кожного гравця, принципи утворення та розподілу виграшних фондів, можливість або неможливість попередніх домовленостей.
Головною задачею, яку розглядає теорія ігор, є задача про прийняття рішень гравцями в умовах, коли їхні інтереси є протидіючими.
Математична модель ігрової ситуації повинна містити: перелік гравців, множини можливих варіантів поведінки кожного гравця, функції виграшу кожного гравця, правила поведінки гравців. Вважається, що вказана інформація є відомою кожному гравцю.
Метою гри є побудова для кожного гравця таких стратегій поведінки, які надають його функції виграшу найбільше значення за умови, що суперники, діючи у власних інтересах, протидіють цьому.
Найбільш простими та теоретично обґрунтованими є скінченні матричні антагоністичні ігри.
Означення. Гра називається скінченною, якщо множини можливих варіантів поведінки кожного з гравців є скінченними множинами.
Означення. Гра називається антагоністичною (або грою з нульовою сумою), якщо в кожному турі гри сумарний виграш одних гравців дорівнює сумарному програшу інших.
Означення. Ігри з двома учасниками називають двосторонніми.
Далі будемо розглядати двосторонні ігри.
Для описання такої гри достатньо знати лише матрицю виграшів або програшів одного з гравців. При розв’язанні таких задач ключову роль відіграє принцип мінімакса.
Принцип мінімакса. У грі з розумним суперником необхідно намагатись, щоб ваш виграш був якомога більшим навіть при найгіршій для вас поведінці суперника.
В ігрових задачах розрізняють дві різні тактики поведінки гравців: чисті стратегії та змішані стратегії. В першому випадку гравець заздалегідь визначає, як саме він буде грати в кожному турі та на протязі всієї гри строго дотримується обраного плану. У другому випадку гравець обирає наступний хід випадково, але згідно з деяким ймовірносним законом розподілу.
Ключовою теоремою в цьому розділі є теорема Неймана.
Теорема 6.1. Для будь-якої скінченої матричної антагоністичної гри існують змішані стратегії поведінки гравців, які забезпечують їм найбільший середній виграш в умовах протидії суперників.
Розглянемо як застосовується ця теорема на прикладі.
6.1. Задача про боротьбу за ринок збуту
Постановка задачі.
Дві виробничі фірми реалізують на
одному ринку продукцію однакового
призначення, тобто конкурують. Хоча
призначення продукції й однакове, вона
може бути різних типів, які відрізняються
споживчими характеристиками. Перша
фірма може випускати продукцію типів
![]() ,
а друга – типів
,
а друга – типів
![]() .
Для простоти будемо вважати, що
собівартість та ціна всіх типів продукції
однакова. Маркетологи з’ясували, що
на даному ринку можна продати N
одиниць товару, причому, якщо перша
фірма випустить продукцію типу
.
Для простоти будемо вважати, що
собівартість та ціна всіх типів продукції
однакова. Маркетологи з’ясували, що
на даному ринку можна продати N
одиниць товару, причому, якщо перша
фірма випустить продукцію типу
![]() ,
а друга – типу
,
а друга – типу
![]() ,
то буде реалізовано
,
то буде реалізовано
![]() одиниць товару
одиниць товару
![]() і
і
![]() одиниць товару
одиниць товару
![]() ,
де
,
де
![]() .
Потужності кожної фірми дозволяють їй
одній цілком задовольнити попит.
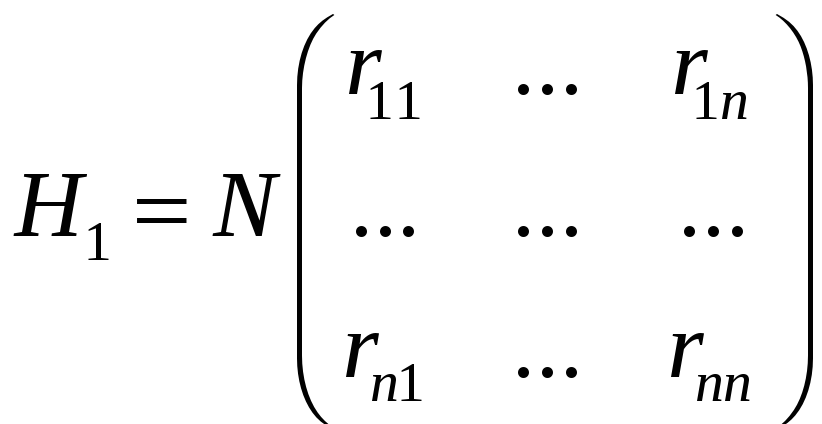
Вважаючи, що доход від реалізації
одиниці товару дорівнює 1, одержуємо
матрицю виграшів першої фірми:
.
Потужності кожної фірми дозволяють їй
одній цілком задовольнити попит.
Вважаючи, що доход від реалізації
одиниці товару дорівнює 1, одержуємо
матрицю виграшів першої фірми:
 .
.
Тоді матриця виграшів другої фірми буде такою:
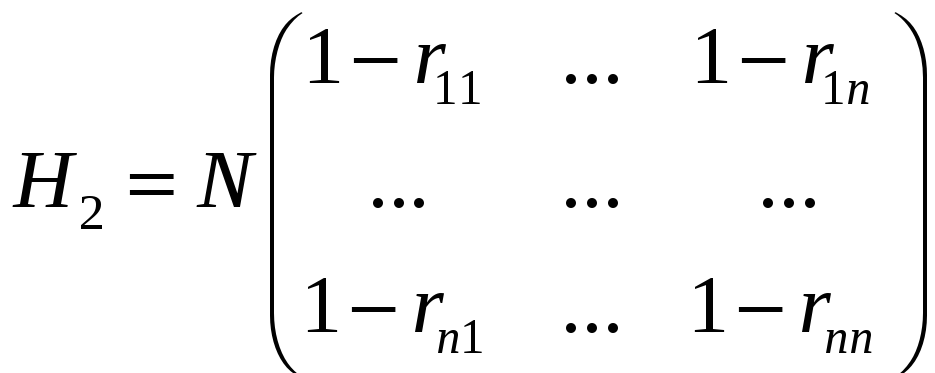 .
.
Оскільки в будь-якому випадку сума доходів фірм дорівнює N, то на скільки збільшиться доход одної фірми, на стільки ж зменшиться доход другої фірми. Отже, ми маємо двосторонню скінчену антагоністичну гру і можемо застосувати до її розв’язку теорему Неймана. Щоб одержати кінцевий результат – оптимальні стратегії фірм – розглянемо числовий приклад.
Нехай N=10,
n=5,
 .
Можна безпосередньо застосовувати
теорему Неймана до цієї матриці. Однак
гру можна значно спростити, якщо
проаналізувати матрицю. Перш за все
зауважимо, що кожен елемент першого
рядка є більшим за відповідний елемент
п’ятого рядка. Отже, першій фірмі немає
сенсу випускати продукцію типу
.
Можна безпосередньо застосовувати
теорему Неймана до цієї матриці. Однак
гру можна значно спростити, якщо
проаналізувати матрицю. Перш за все
зауважимо, що кожен елемент першого
рядка є більшим за відповідний елемент
п’ятого рядка. Отже, першій фірмі немає
сенсу випускати продукцію типу
![]() ,
оскільки тип
,
оскільки тип
![]() ,
очевидно, дає кращі результати. Це
дозволяє викреслити з матриці
,
очевидно, дає кращі результати. Це
дозволяє викреслити з матриці
![]() п’ятий рядок. Аналогічні міркування
дозволяють також викреслити ще декілька
рядків та стовпчиків. Отже, після всіх
спрощень одержимо матрицю
п’ятий рядок. Аналогічні міркування
дозволяють також викреслити ще декілька
рядків та стовпчиків. Отже, після всіх
спрощень одержимо матрицю
 ,
яка означає, що перша фірма обмежується
лише типами
,
яка означає, що перша фірма обмежується
лише типами
![]() і
і
![]() ,
а друга – типами
,
а друга – типами
![]() і
і
![]() .
Згідно з теоремою Неймана, будемо
будувати змішані стратегії. Позначимо
через p ймовірність
того, що перша фірма обере тип
.
Згідно з теоремою Неймана, будемо
будувати змішані стратегії. Позначимо
через p ймовірність
того, що перша фірма обере тип
![]() .
Через q
позначимо ймовірність того, що друга
фірма обере тип
.
Через q
позначимо ймовірність того, що друга
фірма обере тип
![]() .
Тоді середній очікуваний доход першої
фірми складе
.
Тоді середній очікуваний доход першої
фірми складе
![]() .
Керуючись принципом мінімакса, знайдемо
.
Керуючись принципом мінімакса, знайдемо
 .
Аналогічні обчислення для другої фірми
дають
.
Аналогічні обчислення для другої фірми
дають
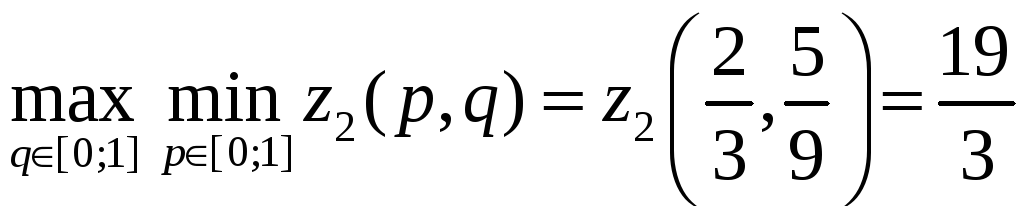 .
Отже, остаточний висновок такий. Перша
фірма повинна випадково з ймовірностями
.
Отже, остаточний висновок такий. Перша
фірма повинна випадково з ймовірностями
![]() та
та
![]() або планомірно у пропорції 2:1 випускати
продукцію типів
або планомірно у пропорції 2:1 випускати
продукцію типів
![]() і
і
![]() ,
а друга фірма також випадково з
ймовірностями
,
а друга фірма також випадково з
ймовірностями
![]() та
та
![]() або
планомірно у пропорції 5:4 випускати
продукцію типів
або
планомірно у пропорції 5:4 випускати
продукцію типів
![]() і
і
![]() .
При цьому середні очікувані доходи
фірм будуть становити
.
При цьому середні очікувані доходи
фірм будуть становити
![]() та
та
![]() грошових одиниць.
грошових одиниць.
Тема 7. Імітаційне моделювання
Імітаційне моделювання набуло значного практичного значення лише останнім часом. Це пов’язане з тим, що імітаційні моделі використовують у тих випадках, коли застосування прямих методів дослідження пов’язане зі значними технічними та теоретичними труднощами. Для високоадекватних імітацій потрібні сучасні високошвидкісні комп’ютери. До класу імітаційних засобів моделювання належить широко відомий метод Монте-Карло. Детальне викладення цього матеріалу див. у [9].
Метою імітаційного моделювання є створення алгоритму, який, по-перше, з тією чи іншою точністю описував би поведінку досліджуваного об’єкта, а по-друге, міг бути практично реалізованим на сучасній комп’ютерній базі за реальний часовий термін. Отже головними принципами розробки імітаційної моделі є такі принципи.
-
Імітуюча модель повинна відтворювати головні риси та особливості об’єкта, який вона імітує.
-
Інформаційно змістовна імітація повинна бути здійсненою в реальні сроки і за реальні кошти.
-
Імітуюча модель повинна бути суттєво простішою за оригінал.
-
Необхідно мати методику оцінювання точності імітації.
-
При застосуванні імітаційної моделі слід знати множини припустимих значень параметрів оригінала, при яких імітатор працює адекватно до оригінала.
Поширеним методом імітації систем із неперервними змінними є метод дискретизації змінних. Наведемо приклад.
Широко відомим у теорії динаміки інформації є системи диференціальних рівнянь, які описують динаміку розповсюдження п типів інформації на деякій території D. Ці рівняння мають такий вигляд:

![]()
Тут
![]() – концентрація інформації
– концентрація інформації
![]() -го
типу в момент часу t і
в точці з координатами
-го
типу в момент часу t і
в точці з координатами
![]() .
Ця система є нелінійною системою
диференціальних рівнянь із частковими
похідними і є дуже складною для
теоретичного дослідження. Розв’язати
її у явному вигляді взагалі немає надії.
Але, застосувавши скінченно-різнецеві
схеми, можна сконструювати обчислювально
простий імітатор, який дозволить
аналізувати життя системи, використовуючи
можливості сучасних комп'ютерів.
Наприклад, можна в рівняннях системи
замінити похідні їхніми скінченно-різнецевими
аналогами і одержати таку систему
рекурентних рівнянь:
.
Ця система є нелінійною системою
диференціальних рівнянь із частковими
похідними і є дуже складною для
теоретичного дослідження. Розв’язати
її у явному вигляді взагалі немає надії.
Але, застосувавши скінченно-різнецеві
схеми, можна сконструювати обчислювально
простий імітатор, який дозволить
аналізувати життя системи, використовуючи
можливості сучасних комп'ютерів.
Наприклад, можна в рівняннях системи
замінити похідні їхніми скінченно-різнецевими
аналогами і одержати таку систему
рекурентних рівнянь:
![]()
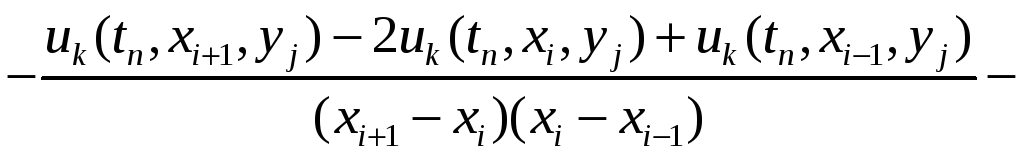
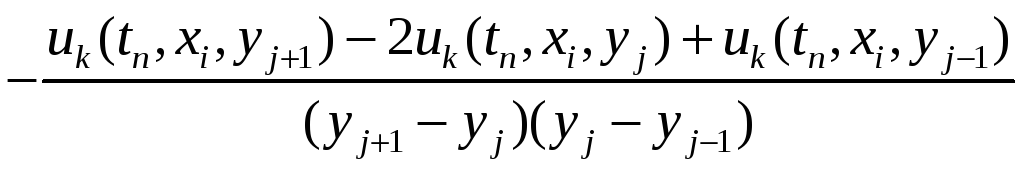 .
.
Ці формули дозволяють поступово, крок за кроком, імітувати розповсюдження інформації, не розв’язуючи складних рівнянь. На сучасних комп'ютерах ця система реалізується за короткі проміжки часу і дозволяє приблизно відтворювати реальні сценарії. З теорії наближених обчислень відомо, що подібні різницеві схеми збігаються до точного розв’язку основної системи. Відомі також оцінки точності наближення. Отже, наведена схема є імітаційною моделлю процесу розповсюдження інформації.
Методи імітаційного моделювання можуть з успіхом використовуватись для прогнозування поведінки досліджуваного об’єкта в майбутньому. Наведемо такий приклад. У книзі [3, c.330] наведено регресійну модель залежності темпу інфляції INF(t) від нього самого в попередній момент часу та рівня безробіття U(t).
![]()
Тут E(1),
E(2),…
– незалежні центровані
Гаусові випадкові величини з невідомою
дисперсією. Якщо за оцінку цієї дисперсії
обрати квадрат абсолютної похибки
моделі
![]() ,
то одержимо рекурентну закономірність:
,
то одержимо рекурентну закономірність:
![]()
Тут е(1), е(2),… – незалежні центровані та нормовані Гаусові випадкові величини. Припустимо, що уряд склав прогноз коливань рівня безробіття на моменти часу T+1,…,T+h. Необхідно з'ясувати, до яких коливань темпу інфляції це може привести. Імітуючи на комп'ютері значення e(T+1),…,e(T+h), користуючись планом коливань рівня безробіття u(T+1),…,u(T+h) та початковим значенням INF(T), одержимо одну з можливих траєкторій розвитку темпу інфляції INF(T+1),…,INF(T+h). Оскільки на поведінку темпу інфляції впливають випадкові складові E(t), то для побудови прогнозу однієї траєкторії недостатньо. Але комп'ютер дозволяє імітувати велику кількість траєкторій. Зімітувавши, скажімо, сто траєкторій, ми матимемо необхідний статистичний матеріал, який дозволить побудувати, наприклад, усереднений прогноз або приблизно обчислити ймовірність виходу темпу інфляції за певний рівень.
Отже виникає комплекс модельних робіт. Спочатку на основі статистичних даних МНК-методом будується регресійна модель ретроспективного плану, а потім на її основі за допомогою імітацій будується перспективна модель.
Тема 8. Математичне моделювання
стохастичних систем
Моделювання стохастичних систем займає окреме місце в теорії моделювання. Моделювання поведінки об’єктів в умовах неповної визначеності суттєво відрізняється від моделювання детермінованих систем. Навіть саме поняття моделі випадкового об’єкта потребує нового визначення. В дослідницькій практиці результатом стохастичного експерименту є, як правило, або число, або траєкторія. Це наводить на думку, що математичною моделлю стохастичного експерименту може бути функція одного або декількох аргументів, один із яких – це випадкові обставини, що впливають на результат. Але в переважній більшості випадків дослідникові невідомий ані вид цієї функції, ані множина можливих значень випадкової змінної. Тому намагатись використовувати функції від випадкових змінних для моделювання стохастичних систем дуже проблематично. З цих причин при моделюванні стохастичних систем у ролі моделей частіш використовують не самі випадкові величини або випадкові процеси, а їхні закони розподілу. Отже, коли ми будемо говорити про побудову математичної моделі випадкового експерименту, ми матимемо на увазі побудову ймовірнісного закону розподілу випадкової величини або випадкового процесу, що задають результат цього експерименту.
