LEC_17_rus

Лекция 17. Вычисление интеграла Римана

План

1. Формула Ньютона-Лейбница

2. Метод интегрирования по частям

3. Метод замены переменной

4. Интеграл от четных (нечетных), периодических функций

1. Формула Ньютона-Лейбница

Теорема 1 (Основная теорема интегрального исчисления). Если функция _{непрерывна на , то она имеет первообразную на этом сегменте.}

_{Доказательство. Рассмотрим функцию на . Поскольку непрерывна в каждой точке , то по теореме о дифференцировании интеграла с переменным верхним пределом для будет выполняться равенство:}

_,

_{а потому является первообразной для на , что и нужно было доказать.}

_{Пусть непрерывна на и - одна из первообразных для . Тогда}

_.

_{Действительно, по основной теореме интегрального исчисления функция также является одной из первообразных для . Две первообразные для одной функции могут отличаться лишь на постоянную, то есть:}

_{. (10)}

_{Надо определить постоянную . Учитывая равенство (10), имеем:}

_,

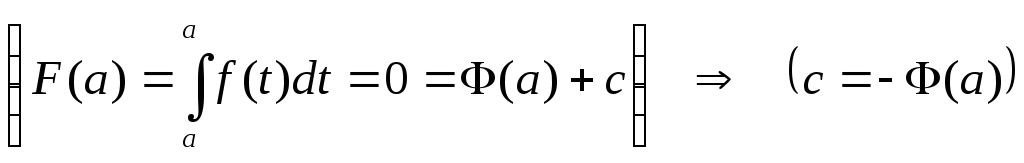_{и формула (10) будет иметь вид:}

_{. (20)}

_{Пусть теперь . Тогда, с одной стороны,}

_{, (30)}

_{а с другой стороны, учитывая (20),}

_{. (40)}

_{Тогда из (30) и (40) получим:}

_,

_{что и нужно было доказать.}

Теорема 2. Пусть _{интегрируема на и - одна из первообразных для на . Тогда}

_{. (50)}

_{Формула (50) называется формулой Ньютона-Лейбница.}

Доказательство. Пусть _{- произвольное разбиение .}

_{. (60)}

_{Функция на каждом частичном сегменте удовлетворяет теореме Лагранжа, поэтому:}

_{. (70)}

_{Учитывая формулу (70), формула (60) будет иметь вид:}

_{. (80)}

_{Правая часть (80) - это интегральная сумма для функции , которая отвечает разбиению . Поскольку функция по условию теоремы является интегрируемой на , то существует и :}

_.

2. Метод интегрирования по частям

Теорема 3. Пусть функции _{, , , определены и непрерывны на . Тогда}

_{, (90)}

_{или иначе:}

_.

_{Доказательство. Поскольку} функции _{, , , непрерывны на , то каждый интеграл в (90) существует. Поскольку}

_,

_{то функция} - это одна из первообразных для функции _{. Тогда по формуле Ньютона-Лейбница:}

_{что и нужно было доказать.}

_{Пример.}

_.

3. Метод замены переменной

Теорема 4. Пусть нужно вычислить _{, где} - непрерывна на _{. Пусть} , и удовлетворяет следующим условиям:

1. определена и непрерывна на _;

2. непрерывна на _;

3. ,

тогда

_{. (100)}

_{Доказательство. Оба интеграла в (100) существуют. Пусть} - первообразная для на _{. Тогда} - первообразная для _{на . По формуле Ньютона-Лейбница}

_;

.

Замечание. Пусть функция определена и непрерывна на сегменте _{, к тому же . Функция} определена, непрерывна и имеет непрерывную на _{, при этом} , и принимает свои значения в _{, тогда имеет место формула (100), то есть значения} могут выходить за границы _.

_{Пример. При вычислить}

4. Интеграл от четных (нечетных), периодических функций

_{Утверждение 1. Пусть} - периодическая функция с периодом . Тогда

_для .

_{Утверждение 2. Пусть} - интегрируема по Риману на _{и является нечетной на} . Тогда

_.

_{Утверждение 3. Пусть} - интегрируема по Риману на _{и является четной на} . Тогда

_.

_{Вопросы}

1. Основная теорема интегрального исчисления. Доказать.

2. _{Вывести формулу Ньютона-Лейбница.}

3. _{Методы вычисления определенного интеграла Римана.}

4. _{Что можно сказать об определенном интеграле Римана от периодической функции?}

5. _{Что можно сказать об определенном интеграле Римана от четной функции на сегменте, который является симметричным относительно начала координат?}

6. _{Что можно сказать об определенном интеграле Римана от нечетной функции на сегменте, который является симметричным относительно начала координат}