Лекция 14. Неопределенный интеграл и его свойства План
Понятие первообразной функции. Свойства первообразной
Понятие неопределенного интеграла, свойства неопределенного интеграла
Метод замены переменной для вычисления неопределенного интеграла
Метод интегрирования по частям
Интегрирование рациональных функций. Метод неопределенных коэффициентов
1. Понятие первообразной функции. Свойства первообразной
Во многих вопросах науки и техники возникает необходимость восстанавливать функцию по ее известной производной.
Будем говорить, что
функция 
в интервале 
называется первообразной
функцией для функции
,
если
.
(1.1)
Пусть 
— первообразная для 
,
тогда любая функция 
,
где 
,
также будет первообразной для 
.
Действительно,
.
Таким образом, если функция имеет первообразную, то она имеет бесконечное множество первообразных.
Теорема 1.
Любые две первообразные функции 
отличаются на постоянную.
Доказательство.
Пусть 
и
- первообразные для 
.
Это означает, что
и 
для 
.
Рассмотрим функцию 
.
Для нее
.
Везде дальше произвольную
постоянную будем обозначать 
.
2. Понятие неопределенного интеграла, свойства неопределенного интеграла
Определение 1.
Пусть функция 
определена на 
.
Множество всех первообразных для функции
называется неопределенным интегралом
для 
и обозначается 
(при этом 
называется подинтегральным выражением):
,
где 
—
одна из первообразных функции 
,
.
Равенство интегралов
=
понимается как равенство множеств первообразных.
Пусть функции 
,
,
определены на 
,
а 
,
,
— их соответствующие первообразные на
.
Через 
будем обозначать
дифференциалы соответствующих функций.
Тогда
;
;
,
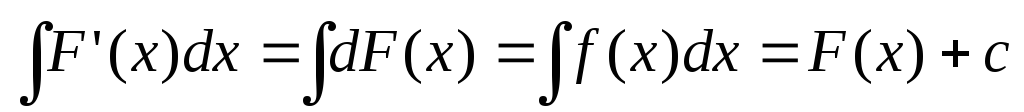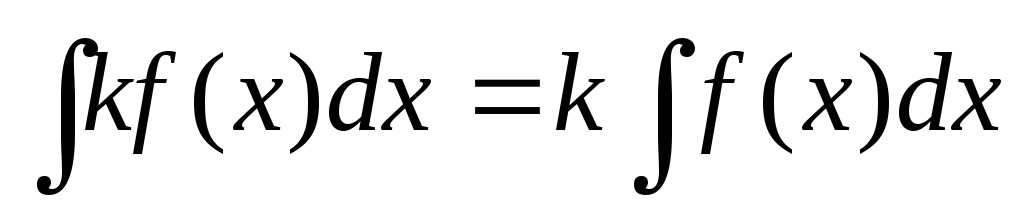де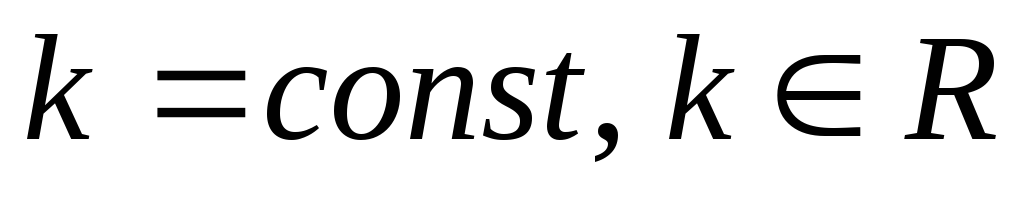 
;
.
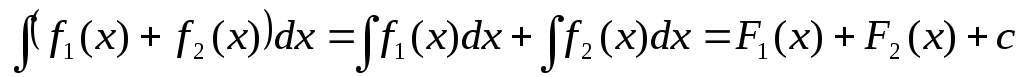Докажем свойство 4:
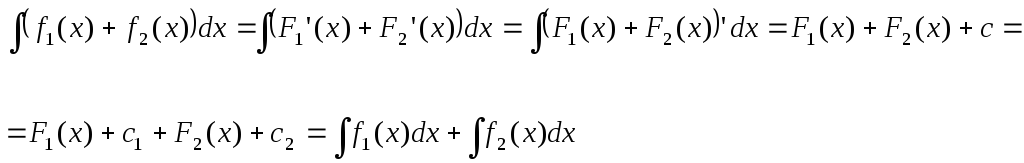
Возникает вопрос: каждая ли функция имеет первообразную? Для ответа на этот вопрос рассмотрим пример.
Пример.
Проверим, имеет ли первообразную 
функция 
.
Если первообразная существует, то
1) поскольку для 
,
то первообразная должна бы была иметь
вид: 
;
2) поскольку для 
,
то первообразная должна бы была иметь
вид: 
,
т.е.
.
Поскольку 
непрерывна в точке 
,
то
.
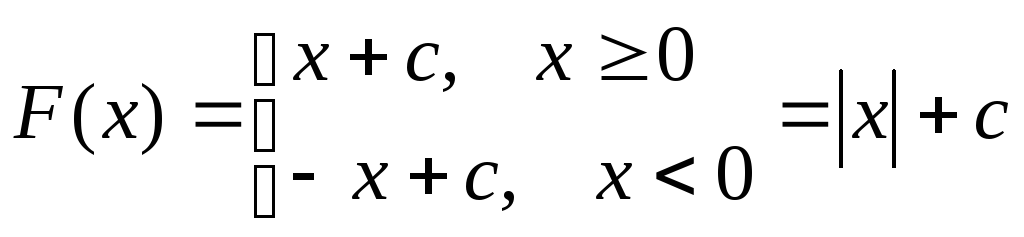Но полученная функция не
может быть первообразной для функции
,
потому что является недифференцированной
в точке 
.
Замечание. Из теоремы Дарбу вытекает, что производная не может иметь разрывов первого рода. Таким образом, если на каком-то интервале функция имеет точки разрыва І рода, у нее не существует первообразной (неопределенного интеграла). Но функция может иметь разрывы и одновременно иметь первообразную, то есть непрерывность не является необходимым условием существования первообразной.
Основная теорема
интегрального исчисления.
Пусть функция 
определена и непрерывна на 
.
Тогда 
имеет первообразную на этом интервале.
При вычислении неопределенного
интеграла легко проверяется правильность
полученного результата с помощью формулы
(1.1): производная от найденной первообразной
должна совпадать с данной функцией 
.