Лекція 13. Необхідна і достатні умови локального екстремума функції План

1. Стаціонарні точки функції. Необхідна умова локального екстремума функції

2. Перша достатня умова локального екстремума

3. Друга і третя достатні умови локального екстремума

4. Найменше й найбільше значення функції на сегменті

5. Опуклі функції і точки перегину

1. Стаціонарні точки функції. Необхідна умова локального екстремума функції

_{Визначення 1.} Нехай функція визначена на _{. Точка називається стаціонарною точкою функції , якщо диференційована в точці і .}

Теорема 1 (необхідна умова локального екстремума функції). Нехай функція визначена на _{і має в точці локальний екстремум. Тоді виконується одна з умов:}

1. функція _{не має в точці похідної;}

2. функція _{має в точці похідну і .}

_{Таким чином, для того, щоб знайти точки, які є підозрілими на екстремум, треба знайти стаціонарні точки функції і точки, в яких похідна функції не існує, але які належать області визначення функції.}

_{Приклад. Нехай . Знайти для неї точки, які є підозрілими на екстремум. Для вирішення поставленої задачі, в першу чергу, знайдемо область визначення функції: . Знайдемо тепер похідну функції:}

_.

_{Точки, в яких похідна не існує: . Стаціонарні точки функції:}

_.

_{Оскільки і , і належать області визначення функції, то вони обидві будуть підозрілими на екстремум. Але для того, щоб зробити висновок, чи буде там дійсно екстремум, треба застосовувати достатні умови екстремума.}

2. Перша достатня умова локального екстремума

Теорема 1 (перша достатня умова локального екстремума). Нехай функція визначена на _{і диференційована нацьому інтервалі скрізь за винятком, можливо, точки , але в цій точці функція є неперервною. Якщо існують такі правий і лівий напівоколи точки , в кожному з яких зберігає означений знак, то}

_{1) функція має локальний екстремум в точці , якщо приймає значення різних знаків в відповідних напівоколах;}

_{2) функція не має локальний екстремум в точці , якщо зправа і зліва від точки має однаковий знак.}

_{Доказ. 1) Припустимо, що в напівоколі похідна , а в .}

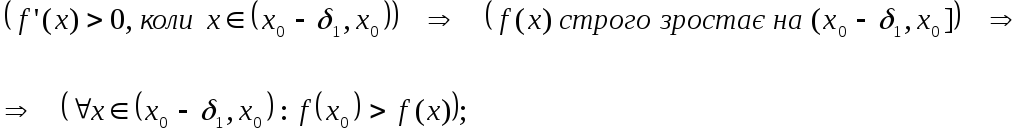
_{Таким чином в точці функція має локальний екстремум, а саме – локальний максимум, що й потрібно було довести.}

_{2) Припустимо, що зліва і справа від точки похідна зберігає свій знак, наприклад, . Тоді на і функція строго монотонно зростає, тобто:}

_,

_.

_{Таким чином екстремума в точці функція не має, що й потрібно було довести.}

_{Зауваження 1. Якщо похідна при проходженні через точку змінює знак з «+» на «-», то в точці функція має локальний максимум, а якщо знак змінюється з «-» на «+», то локальний мінімум.}

_{Зауваження 2. Важливою є умова неперервності функції в точці . Якщо ця умова не виконується, то теорема 1 може не мати місця.}

_{Приклад. Нехай розглядається функція (рис.1):}

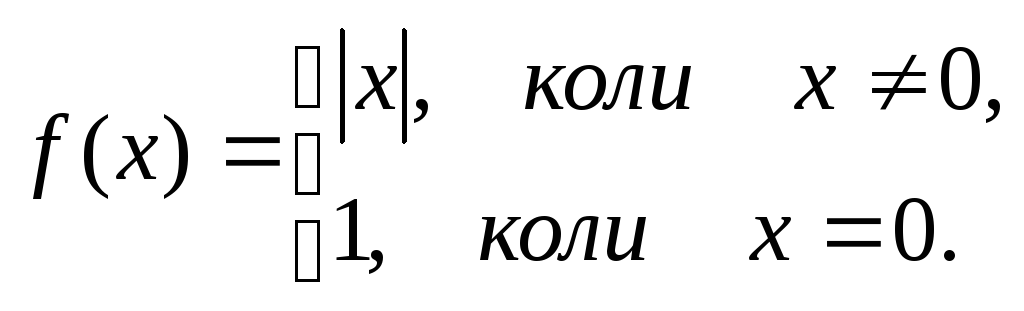
Ця функція визначена на _{і неперервна скрізь, крім точки , де вона має усувний розрив. При проходженні через точку змінює знак з «-» на «+», але локальний мінімум в цій точці функція не має, а має локальний максимум за визначенням. Дійсно, навколо точки можна побудувати такий окіл, що для всіх аргументів з цього околу значення функції буде меньшим за значення . Теорема 1 не спрацювала тому, що в точці функція мала розрив.}

_{Зауваження 3. Перша достатня умова локального екстремума не може бути використаною, коли похідна функції змінює свій знак в кожному лівому і кожному правому напівоколі точки .}

_{Приклад. Нехай розглядається функція:}

_{Оскільки , то , а тому , але . Таким чином:}

_,

_{тобто в точці функція має локальний мінімум за визначенням. Подивимось, чи спрацює тут перша достатня умова локального екстремума.}

_{Для :}

_.

Для першого доданку правої частини отриманої формули маємо:

_,

_{а тому в малому околі точки знак похідної визначається знаком другого доданку, тобто:}

_,

_{а це означає, що в будь-якому околі точки буде приймати як додатні, так і від’ємні значення. Дійсно, розглянемо довільний окіл точки : . Коли , то (рис.2), а змінює свій знак тут нескінченно багато разів. Таким чином, не можна використовувати в наведеному прикладі першу достатню умову локального екстремума.}