Лекція 14. Невизначений інтеграл і його властивості План

1. Поняття первісної функції. Властивості первісної

2. Поняття невизначеного інтегралу, властивості невизначеного інтегралу

3. Метод заміни змінної для обчислення невизначеного інтегралу

4. Метод інтегрування за частинами

5. Інтегрування раціональних функцій. Метод невизначених коефіцієнтів

1. Поняття первісної функції. Властивості первісної

У багатьох питаннях науки й техніки виникає необхідність відновлювати функцію по її відомій похідній.

Будемо говорити, що функція в інтервалі називається первісною функцією для функції , якщо

. (1.1)

Нехай — первісна для , тоді будь-яка , де , також буде первісною для . Дійсно,

.

Таким чином, якщо функція має первісну, то вона має безліч первісних.

Теорема 1. Будь-які дві первісні функції відрізняються на сталу.

Доказ. Нехай і - первісні для . Це означає, що

і для .

Розглянемо функцію . Для неї

.

Скрізь далі довільну сталу будемо позначати .

2. Поняття невизначеного інтегралу, властивості невизначеного інтегралу

Визначення 1. Нехай функція визначена на . Множина усіх первісних для функції називається невизначеним інтегралом для і позначається (при цьому називається підінтегральним виразом):

,

де — одна з первісних функції , .

Рівність інтегралів

=

розуміється як рівність множин первісних.

Нехай функції , , визначені на , а , , — їх відповідні первісні на . Через будемо позначати диференціали відповідних функцій. Тоді

1. ;

2. ;

3. , де ;

4. .

Доведемо властивість 4:

Виникає питання: чи кожна функція має первісну? Для відповіді на це питання розглянемо приклад.

Приклад. Перевіримо, чи має первісну функція . Якщо первісна існує, то

1) оскільки для , то первісна повинна б була мати вигляд: ;

2) оскільки для , то первісна повинна б була мати вигляд: , тобто

.

Оскільки неперервна в точці , то

.

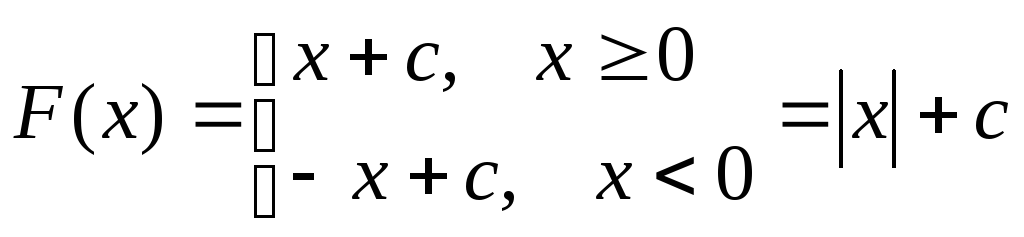Але отримана функція не може бути первісною для функції , бо є недиференційованою в точці .

Зауваження. З теореми Дарбу витікає, що похідна не може мати розривів першого роду. Отже, якщо на якомусь інтервалі функція має точки розриву І роду, в неї не існує первісна (невизначений інтеграл). Але функція може мати розриви і одночасно мати первісну, тобто неперервність не є необхідною умовою існування первісної.

Основна теорема інтегрального числення. Нехай функція визначена і неперервна на . Тоді має первісну на цьому інтервалі.

При обчисленні невизначеного інтеграла легко перевіряється правильність отриманого результата за допомогою формули (1.1): похідна від знайденої первісної повинна співпадати з поданою функцією .

3. Метод заміни змінної для обчислення невизначеного інтегралу

Теорема 2. Нехай функція визначена на інтервалі і має тут первісну , і нехай функція має похідну скрізь в області визначення і приймає значення в . Тоді функція має первісну . Інакше кажучи, нехай треба обчислити інтеграл

.

У багатьох випадках вдається в якості нової змінної вибрати таку функцію , щоб підінтегральний вираз можна було представити у вигляді:

,

де — більш зручна для інтегрування функція, ніж .Тоді достатньо знайти інтеграл

,

щоб з нього підстановкою отримати шуканий інтеграл:

.

Доказ. Перевіримо, що отримана функція дійсно буде первісною для :

.

Простіше всього заміна проводиться тоді, коли у поданому виді підінтегрального виразу в якості множника вже присутня похідна від нової змінної (хоча так буває далеко не завжди).

Приклад. .

Підінтегральний вираз поряд з містить у якості множника . Це говорить на користь заміни: .

.