Navch._posibnuk_Ivaschyk

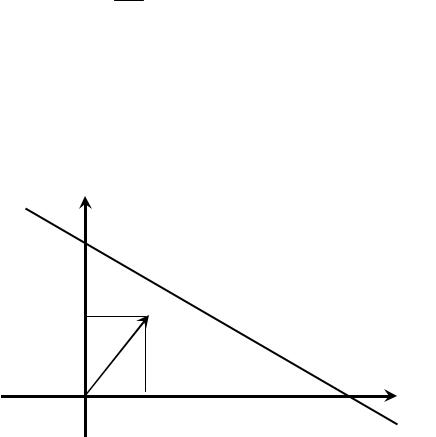
z = c0			+ c1x1 + c2 x2					(extr),
a11x1 + a12 x2 ≤ b1 ,
............................
			+ ak 2 x2				≤ bk ,
ak1x1
ak +11x1 + ak +12 x2 ≤ bk +1 ,
.............................
		x	+ a		x		≤ b ,
a				m2		2
	m1 1						m
x1		≥ 0,		x2			≥ 0.

Розглянемо основні етапи знаходження розв’язку задач ЛП графічним методом:

1) На координатній площині Х10Х2 будуємо граничні прямі (рис.2.2.2), які відповідають системі обмежень задачі:

ai1 x1 + ai 2 x2 = bi , i =1, m.

2) Визначаємо півплощини, які є розв’язками нерівностей. Для цього беремо координати точки з довільної півплощини і підставляємо в нерівність. Якщо нерівність справджується, то півплощина розв’язків направлена в сторону вибраної точки, якщо ж не справджується, то в протилежнусторону.

x2

с2	→ ai1x1 + ai2 x2 = bi
	N

с1 x1

Рисунок 2.2.2

3) Знаходимо область, де перетинаються всі півплощини розв’язків – многокутник розв’язків. Якщо перетин – непорожня множина, то переходимо до наступного етапу. В протилежному випадку робимо висновок, що задача не маєрозв’язку.

61

→

4) Будуємо вектор нормалі N , початок якого знаходиться в точці (0,0), а кінець в точці (c1 ,c2 ) (коефіцієнти при невідомих в цільовій

функції). Вектор нормалівказує напрямок зростання функції.

5) Перпендикулярно до вектора нормалі будуємо лінію рівнів c1 x1 + c2 x2 = const . Для зручності знаходження оптимальних точок лінію

рівнів будуємо так, щоб вона мала спільні точки з многокутником розв’язків (перетинала многокутникрозв’язків).

6)Визначаємо оптимальні точки. Для цього лінію рівнів паралельно переносимо в напрямку вектора нормалі. Остання вершина многокутника, яку перетне лінія рівнів, буде точкою максимуму. Потім лінію рівнів паралельно переносимо в напрямку, протилежному напрямку вектора нормалі. Остання вершина многокутника розв’язків, яку перетне лінія рівнів в цьому випадку, є точкоюмінімуму.

7)Знаходимо найбільше та найменше значення функції Z. Для цього підставимо координати оптимальних точок, знайдених шляхом розв’язування систем рівнянь граничних прямих (перетином яких є оптимальна точка), вцільову функцію.

Приклад 2.2. Графічним методом розв’язати задачу лінійного програмування:

Z = 3x1 + 7x2				− 5 (extr),
4x		− 3x			≤12,
	1			2		≤130,
10x1 +13x2
− 6x1 + 8x2						≤ 48,
		+ 5x2 ≥10,
2x1
4x		− x		≥ 0,
	1		2
x	≥ 0,
1	≥ 0.
x2

♦Розв’язування.

Будуємо граничні прямі, що відповідають нерівностям системи обмежень задачі (кожне обмеження розглядаємо як рівняння). Для побудови довільної прямої нам потрібно дві точки. Якщо права частина рівняння не дорівнює нулю, то для простоти знаходження координат двох точок, через які проходить гранична пряма (наприклад L1), беремо спочатку x1=0 і знаходимо x2: 4·0–3х2=12, звідси –3х2=12, а значить х2=–4. Ми маємо координати однієї точки (0, –4). Потім беремо х2=0 і знаходимо х1: 4х1–3·0=12, звідси 4х1=12, а значить х1=3. Отже,

62

координати другої точки (3,0). Аналогічно знаходимо координати точок для побудови граничних прямих L2, L3 та L4.

В правій частині граничної прямої, що відповідає п’ятому обмеженню – нуль, тому для знаходження координат двох точок цієї прямої один раз візьмемо x1=0, тоді отримаємо, що х2=0. Для визначення координат другої точки беремо довільне значення однієї з невідомих, тільки не 0, наприклад, x1=1 і знаходимо значення х2: 4·1–х2=0, звідси

х2= 4.

L1	:	4x1 −3x2		=12,	(0;−4); (3;0).
L2 :		10x1 +13x2		=130,	(0;10);	(13;0).
L3 :		−6x1 +8x2 = 48,			(0;6); (−8;0).
L4	:	2x1 +5x2		=10,	(0;2);	(5;0).
L5	:	4x1 − x2		= 0,	(0;0);	(1;4).
L6	:	x1	= 0,		вісь	Ox2 .
L7	:	x2	= 0,		вісь	Ox1.

		L2	x2	L5
	Лінія рівнів	10
		6	B			C
						→
		4				N
		2	A
						E
L7
-8			1		3		5
			-4

L3

L1

D

13 x1

L6

L4

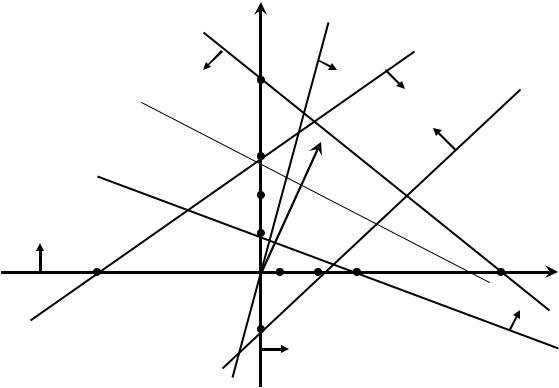
Рисунок 2.2.3

Знаходимо півплощини розв’язків, що відповідають нерівностям системи обмежень. Для цього беремо довільну точку координатної

63

площини, через яку не проходить гранична пряма 4x1 −3x2 =12 (для

простоти розрахунків візьмемо (0,0)) і підставляємо в першу нерівність. Отримаємо 4·0–3·0<12; 0<12, отже, нерівність справджується. А це значить, що півплощина розв’язків, яка відповідає першому обмеженню задачі, розміщена в напрямку точки (0,0). На рисунку вказуємо стрілкою в якому напрямку від прямої L1 розміщена наша півплощина розв’язків. Аналогічні розрахунки проводимо з усіма граничними прямими. Тільки для визначення півплощини розв’язків, що відповідає п’ятому обмеженню, беремо координати довільної точки, що не лежить на прямій, тільки не точку (0,0), оскільки гранична пряма L5 проходить через початок системи координат. Шукаємо спільну область, де перетинаються всі півплощини розв’язків. В нашому випадку многокутникомрозв’язківє фігураABCDE.

Будуємо вектор нормалі N ={(0;0);(3;7)}. Перпендикулярно до нього – лінію рівнів. Паралельно переносимо цю лінію в напрямку вектора нормалі. Останньою вершиною многокутника, яку перетне лінія рівнів є точка С – точка максимуму. Тоді паралельно переносимо лінію рівнів у напрямку, протилежному до напрямку вектора нормалі. Крайньою вершиною, яку перетне лінія рівнів, є точка А – точка мінімуму.

Знайдемо координати оптимальних точок і найбільше та найменше значення функції Z. Точка С лежить на перетині граничних прямих L2 та L3, тому її координати обчислимо, розв’язавши систему рівняньцих граничних прямих:

														13												x	= −				13		x			+13,
10x +13x					2		=		130,			x1	+				x2		=		13,					1				10					2
	1													10
− 6x1		+ 8x2				=			48.			−6x +8x							2		= 48.					−6(−			13			x				+13) +8x					= 48.
																																		2						2
														1														10
x			13														x					13
		= −					x			+13,										= −			x		+13,												13
	1		10						2									1			10			2							x1					= −			x2	+13,
																																					10
			39															79
−78 +					5			x2 +8x2 = 48.													x2 =126.										x2					= 7,97.
																	5

x1 = −1013 7,97 +13 = 2,64,x2 = 7,97.

Ми отримали, що С(2,64; 7,97).

Тоді Zmax = Z (C) = 3 2,64 + 7 7,97 −5 = 7,92 +55,79 −5 = 58,71.

Точка A – перетин L4 та L5. Запишемо систему рівнянь цих граничних прямих ірозв’яжемо її:

64

2x +5x

=10,

2x

+5x

=10,

2x

+5 4x =10,

1

2

1

2

1

1

4x1 − x2 = 0.

x2

= 4x1.

x2

= 4x1.

22x =10,

x

= 0,45,

1

4x1.

1

= 4 0,45 =1,8.

x2

=

x2

Отже,

А(0,45; 1,8).

А Zmin = z(A) = 3 0,45 + 7 1,8 −5 =1,35 +12,6 −5 = 8,95.♦

При розв’язуванні задач лінійного програмування графічним методомможливітаківипадки:

Лінія x2 Zmax рівнів

Zmin

В

→

N

А

О x1

Рисунок 2.2.4

В даному випадку функція Z досягає найменшого значення в точціА, а найбільшого вточціВ.

x2 Zmax В

Zmin

→ C

N

А

ОЛінія x1

Рисунок 2.2.5	рівнів

65

Функція Z досягає найменшого значення в точці А, а найбільшого на відрізку ВС, тобто існує неєдиний оптимальний (максимальний) розв’язок задачі (аналітичним критерієм неєдиності є пропорційність коефіцієнтів при невідомих в цільовій функції коефіцієнтам при невідомих рівняння граничної прямої, на якій лежить відрізок ВС). Щоб знайти найменше значення функції, потрібно знайти координати точки А і підставити в цільову функцію, а щоб знайти найбільше значення функції Z, потрібно в цільову функцію підставити координати довільної точки відрізка ВС. Найпростіше знайти координати кінців відрізка (координати точки перетину граничних прямих), тому знаходимо координати точки В чи точки С і підставляємо вцільову функцію.

Zmax x2

→

N

Zmin

А

О	x1
	Лінія
	рівнів

Рисунок 2.2.6

Функція Z досягає найменшого значення в точці А, а найбільше значення функції рівне безмежності, оскільки многокутник розв’язків необмежений зверху (Zmax = +∞).

66

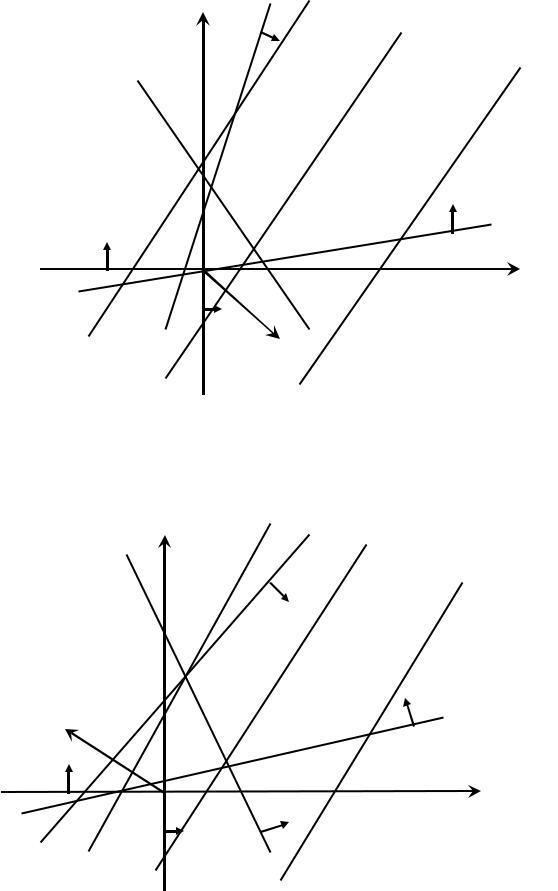
x2 Zmin

Лініярівнів Zmax

О x1

→

N

Рисунок 2.2.7

Найменше значення функції Zmin = −∞, а найбільше значення Zmax = +∞, оскільки многокутник розв’язків необмежений і знизу і зверху.

x2

Zmax

Zmin

Лінія

рівнів

А

→

N

О	x1

Рисунок 2.2.8

67

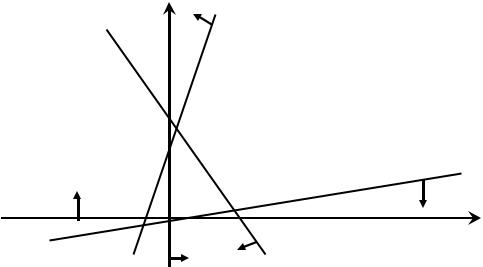
Найменше значення функції Zmin = −∞, оскільки многокутник

розв’язків необмежений знизу, а найбільше значення функція Z досягає в точціА.

x2

x1

О

Рисунок 2.2.9

Ми бачимо, що в даному випадку перетином півплощин розв’язків є порожня множина, тобто система обмежень задачі несумісна (немає жодного розв’язку), тому знайти екстремальні значенняцільової функції неможливо.

2.3.Симплексний метод розв’язування задач лінійного програмування

На відміну від графічного методу, який доцільно застосовувати лише для розв’язування задач лінійного програмування з двома змінними, за допомогою симплекс-методу можна знаходити розв’язки задач ЛП з більшою кількістю невідомих. Процес розв’язування задачі таким методом має ітераційний характер. Обчислювальні процедури (ітерації) одного й того самого типу повторюються в конкретній послідовності за певними правилами до тих пір, доки не буде отримано оптимальний план задачі або з’ясовано, що його не існує.

Симплекс-метод – це поетапна обчислювальна процедура, в основу якої покладено принцип послідовного поліпшення значень цільової функції переходом від одного опорного плану задачі ЛП до іншого.

68

Цей метод можна використовувати для розв’язування задач ЛП, які записані в канонічній формі, тобто:

1)задача ЛП записана в першій стандартній формі (обмеженнярівності);

2)праві частини рівнянь-обмежень (вільні члени) невід’ємні;

3)система рівнянь-обмежень має чітко виділений базис, тобто в кожному рівнянні є невідома з коефіцієнтом 1 і ця невідома відсутня в усіх інших рівняннях системи обмежень. Ці невідомі називаються базисними, а всі інші – вільними;

4)цільова функція залежить тільки від вільних невідомих.

Алгоритм симплексного методу розв’язування задач лінійного програмування складається з таких етапів:

1.Визначення початкового опорного плану задачі лінійного програмування.

2.Побудова симплексної таблиці.

3.Перевірка опорного плану на оптимальність за допомогою чисел нульового рядка симплекс-таблиці. Якщо умова оптимальності виконується, то визначений опорний план є оптимальним, якщо ж не виконується, то переходять до нового опорного плану або встановлюють, що оптимального плану задачі не існує.

4.Перехід до нового опорного плану задачі здійснюється визначенням ключового (генерального) елемента та розрахунком нової симплекс-таблиці.

5.Повторення дій, починаючи з п.3.

Розглянемо детальніше кожен етап цього алгоритму.

1. Визначення початкового опорного плану починають із запису задачі лінійного програмування у канонічній формі. Якщо в системі обмежень є обмеження-нерівності, то до лівої частини обмежень типу «≤» додаємо додаткові невід’ємні невідомі, а від лівих частин обмежень типу «≥» віднімаємо додаткові невід’ємні невідомі. Якщо права частина обмеження від’ємна, то множимо все обмеження на (–1). Якщо цільова функція містить базисні невідомі, то виражаємо їх через вільні з системи обмежень і підставляємо в цільову функцію.

Після зведення задачі до канонічного виду перевіряємо, чи кількість базисних невідомих дорівнює кількості рівнянь системи обмежень. Якщо ця рівність виконується, то початковий опорний план визначається безпосередньо без додаткових дій. Для цього вільні невідомі прирівнюють до нуля і з кожного рівняння-обмеження зразу отримують значення базисних невідомих, тобто таким чином

69

отримуємо початковий опорний план задачі. Якщо ж кількість базисних невідомих менша від кількості рівнянь-обмежень задачі, то для побудови початкового опорного плану використовують метод штучного базису.

2.Подальший обчислювальний процес та перевірку опорного плану на оптимальність здійснюють з допомогою симплекс-таблиць.

Впершому стовпчику таблиці записуємо номер таблиці (ітерації), в другому стовпчику – номер рядка, в наступному – «Базис» (базисні невідомі), далі – «Опорний план» (значення базисних змінних), а у решті стовпчиків, кількість яких дорівнює кількості невідомих задачі, – відповідні коефіцієнти при невідомих кожного обмеження задачі лінійного програмування.

Звернемо увагу на те, що в нульовому рядочку симплекстаблиці записуємо дані з цільової функції.

3.Перевіряємо опорний план на оптимальність згідно з теоремою.

Теорема (критерій оптимальності симплекс-методу). Якщо цільова функція максимізується (мінімізується) і в нульовому рядку відсутні від’ємні (додатні) числа, за винятком стовпчика «Опорний план», то опорний план є оптимальним.

У процесі перевірки умови оптимальності можливі такі випадки: а) умова оптимальності виконується, а значить опорний план є оптимальним; б) умова оптимальності не виконується, тоді потрібно перейти до

нового опорного плану.

4. Перехід від одного опорного плану до іншого виконується зміною базису, тобто виключенням з базису деякої змінної та введенням замість неї нової з числа вільних невідомих задачі.

Змінну, яку потрібно ввести в базис, визначаємо за елементами нульового рядка. Якщо цільова функція досліджується на мінімум і в нульовому рядку симплекс-таблиці є додатні числа (за винятком стовпчика «Опорний план»), то вибираємо найбільше з цих чисел і невідому, що відповідає цьому числу, вводимо в базис. Якщо ж цільова функція досліджується на максимум і в нульовому рядку симплекс-таблиці є від’ємні числа (за винятком стовпчика «Опорний план»), то вибираємо найменше з них (найбільше по модулю) і невідому, що йому відповідає, вводимо в базис. Стовпець, який відповідає невідомій, що вводиться в базис, називається ключовим.

Для визначення змінної, яка має бути виведена з базису, знаходять відношення елементів стовпця «Опорний план» до

70