Modul-5_ppi

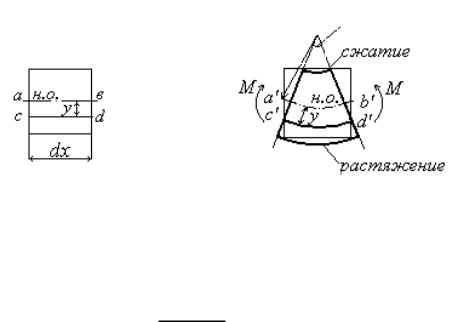
(отрезок ав). Деформированный элемент изображаем в соответствие с гипотезой плоских сечений Я.Бернулли. При этом обозначим: – радиус кривизны нейтральной оси; d – угол взаимного поворота сечений балки.

d

элемент в исходном	элемент в деформированном
состоянии	состоянии

Определим деформацию произвольного волокна балки cd, которое расположено на расстоянии y от нейтральной оси

c d cd . cd

Здесь: cd – исходная длина волокна, c d – длина этого волокна после деформации. Очевидно, что cd ab a b , где a b – длина отрезка искривленной нейтральной оси. Длину этого отрезка можно определить по

формуле a b d (см.	рис). Поскольку	cd a b , исходную	длину
рассматриваемого волокна	представим в виде	cd d , а длину	после

деформации – в виде c d ( y) d . Подставляя эти выражения в формулу для , получим

	y d d		y d		y	.
	d		d

Таким образом, деформация произвольного волокна, расположенного на

расстоянии у от нейтральной оси, определяется по формуле
	y	.	(3)

Физическая сторона задачи. Согласно допущению о ненадавливании продольных волокон друг на друга, рассматриваемое отдельное волокно находится в линейном напряженном состоянии, и закон Гука для него имеет вид

E .
Подставляя в эту формулу выражение (3), получим
E	y	.	(4)

11

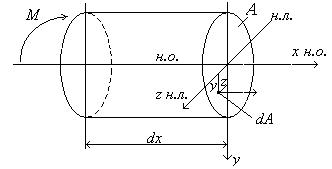
Формулу (4), однако, использовать для определения напряжения нельзя, поскольку неизвестно положение нейтральной оси, от которой задается расстояние до рассматриваемого произвольного волокна – у, а также неизвестна величина радиуса кривизны нейтральной оси – .

Рассмотрим, в этой связи, равновесие выделенного элемента балки (статическая сторона задачи). Причем к левому сечению элемента приложим, изгибающий момент М, а в правом сечении представим этот момент напряжениями . Для этого введем в сечении систему координат: ось x – нейтральная ось балки, ось y – ось симметрии сечения, ось z- нейтральная линия сечения балки (см. рис.). Выделим бесконечно малую площадку dA с положительными координатами y и z и приложим к этой площадке положительные нормальные напряжения , соответствующие положительному моменту М. Тогда элементарная нормальная сила, действующая по площадке dA, будет равна dA, а элементарные моменты относительно осей у и z соответственно составят dMy = dA z и dMz = dA y.

Силы, действующие на элемент балки, представляют собой пространственную систему. Очевидно, что из шести уравнений равновесия для рассматриваемой пространственной системы три уравнения являются тождествами

Y 0;

Z 0;

M x 0 .

Рассмотрим оставшиеся уравнения равновесия.

В уравнение равновесия X 0 войдет только равнодействующая

нормальных напряжений, приложенных к правому сечению элемента, которую определим путем суммирования (интегрирования) элементарных сил dA по площади сечения А. Рассматриваемое уравнение равновесия при этом примет вид

X dA 0.

A

Подставляя в это уравнение соотношение (4) и вынося за знак интеграла величины, которые не зависят от переменной интегрирования, будем иметь

	E y	dA	E	ydA 0 .
A			A

12

	Поскольку	E	0 , получаем	ydA 0 . С другой стороны,	ydA Sz , где Sz –
				A	A

статический момент сечения относительно оси z. Таким образом, из рассмотренного уравнения равновесия следует, что в принятой системе координат Sz=0.

Запишем сумму моментов относительно оси у, суммируя (интегрируя) элементарные моменты dMy по площади сечения

M y dM y z dA 0 .

A A

Используя подстановку (4), получим

			E	y	z dA	E	y z dA 0 .
			A			A
	В этом уравнении	E	0 ,	тогда y z dA 0. Но				y z dA I yz , где Iyz –
					A			A

центробежный момент инерции сечения относительно осей y и z. Отсюда следует, что центробежный момент инерции относительно осей y и z равен нулю ( I yz 0 ).

На основе полученных выше соотношений (Sz=0 и I yz 0 ) можно сделать следующие важные выводы:

1)ось z, совпадающая с нейтральной линией, является главной центральной осью поперечного сечения балки, т.е. при чистом плоском изгибе нейтральная линия совпадает с главной центральной осью сечения;

2)ось х, совпадающая с нейтральной осью балки, является ее

геометрической осью, т.е. при чистом плоском изгибе нейтральная ось совпадает с геометрической осью балки.

Последнее уравнение равновесия для выделенного элемента будет включать в себя изгибающий момент, приложенный к левому сечению, и момент, обусловленный нормальными напряжениями, полученный путем суммирования элементарных моментов dMz

M z M dM z 0.

			A
Из этого уравнения, с учетом (4), получим
M dM z y dA			E y2	dA	E	y2dA .
A	A	A			A

Здесь y2dA I z – момент инерции сечения относительно главной центральной

A

оси z. Подставляя его в выражение для изгибающего момента, будем иметь

13

M E I z .

Отсюда получаем формулу для кривизны оси балки

	1		M		.	(5)
			EIz

Здесь: произведение EIz называют жесткостью сечения балки при изгибе.

Из (5) следует, что при чистом изгибе ось балки будет искривляться по дуге окружности с радиусом .

Синтезируя результаты, полученные на разных этапах решения задачи, подставим (5) в (4)

E y M ,

E I z

откуда получим формулу для нормальных напряжений при чистом изгибе

	M	y	.	(6)
	I z

Здесь: М – изгибающий момент в сечении балки;

Iz – момент инерции сечения относительно главной центральной оси z;

y – координата точки, в которой определяется (расстояние от оси z с соответствующим знаком).

Из формулы (6) следует, что по ширине сечения не изменяется, а по высоте сечения изменяется по линейному закону.

Некоторые замечания

Полученная для нормальных напряжений формула (6) при чистом изгибе является точной (поскольку точно выполняется гипотеза плоских сечений Я.Бернулли). Об этом свидетельствуют результаты расчета методами теории упругости, которые не используют гипотезу Я.Бернулли, а также данные экспериментов.

В случае плоского поперечного изгиба касательные напряжения, возникающие, согласно закону парности, в продольных сечениях балки, параллельных координатной плоскости x-z, приводят к тому, что гипотеза Я.Бернулли не выполняется (поперечные сечения искривляются). Это обусловливает погрешности при определении по формуле (6), однако для балок длинных и средней длины указанная погрешность не превышает (3-5)%. Поэтому формулу (6) применяют также и при плоском поперечном изгибе, при котором изгибающий момент изменяется по длине балки. При этом остаются в силе выводы, касающиеся совпадения нейтральной оси с геометрической осью балки и нейтральной линии с главной центральной осью инерции поперечного сечения балки.

14

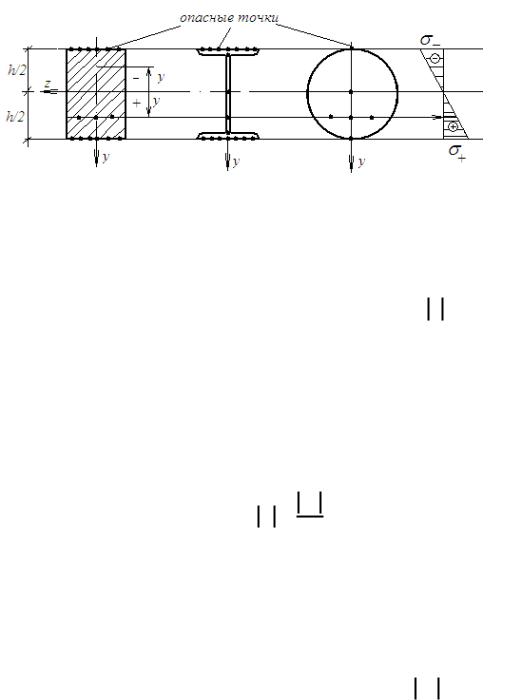
Эпюры и условие прочности по при ППИ

I. Бисимметричные (с двумя осями симметрии) сечения балки

Построим для прямоугольного, двутаврового и кругового сечений балки эпюру , используя формулу для нормальных напряжений (6), полагая, что изгибающий момент в рассматриваемом сечении положительный (М>0). Очевидно, что при разных значениях напряжений эпюры будут иметь одинаковый вид (форму) (см. рис.).

Из приведенной эпюры видно, что максимальные по абсолютной величине напряжения в области растяжения и сжатия одинаковы и действуют в точках, наиболее удаленных от оси, при y=maxy.

Используя подстановку y=maxy , получим по формуле (6) максимальные напряжения в заданном сечении

max

M

max

y

,

либо

max

M

.

I z

I z

max y

В последней формуле знаменатель

I z					Wz
max		y

представляет собой момент сопротивления сечения балки относительно оси z. Таким образом, с учетом этого, максимальные напряжения в заданном произвольном сечении балки будут определяться по формуле

max M .

Wz

Точки, в которых возникают наибольшие по абсолютной величине напряжения, называются опасными.

Условие прочности записывают для наиболее напряженной точки балки. Этой точкой является опасная точка в опасном сечении.

Поскольку опасное сечение балки располагается там, где изгибающий момент по абсолютной величине максимален ( M max M ), напряжения в наиболее напряженной точке будут равны

15

max max max M ,

Wz

а условие прочности для балки по нормальным напряжениям при ППИ

примет вид

	max		M				.	(7)
	Wz

Это условие прочности записано для материала, который одинаково работает на растяжение-сжатие. Если материал по разному сопротивляется растяжению и сжатию необходимо записывать только условие прочности с меньшим значением допускаемого напряжения [ ], как правило, это условии прочности для точки с растягивающими напряжениями (для [+])

	max		M					.	(8)
	Wz

II. Сечения балки с одной осью симметрии (на примере таврового профиля)

Из эпюры видно, что в этом случае максимальные растягивающие и сжимающие напряжения в сечении различные.

Условие прочности для материалов одинаково работающих на растяжение-сжатие будет иметь вид (7). В случае, если материал не одинаково сопротивляется растяжению-сжатию, условие прочности необходимо формулировать для двух точек:

-точки опасной по растяжению (точка н),

-точки опасной по сжатию (точка в)

max

M

max

yн

;

max

M

max

yв

.

I z

I z

Заметим, что для балок, сечение которых имеет одну ось симметрии, выполненных из материалов по разному сопротивляющихся растяжению и сжатию (например, выполненных из бетона), в зависимости от их нагружения и закрепления необходимо решать вопрос об ориентации сечения (полка сверху либо полка снизу). Подумайте об этом.

16

Три типа задач, решаемых на основные условия прочности по нормальным напряжениям при ППИ

I. Проверочный расчет

Задано: все размеры балки (Wz), материал ([ ]) и нагрузка. Требуется: проверить прочность балки по нормальным напряжениям.

Определяются изгибающие моменты в сечениях балки (строятся эпюры М) и проверяется выполнение условия прочности, записанного в форме проверочного расчета

max		M				.	(I)
	WZ

Если условие прочности выполняется, балка, с точки зрения условия прочности по нормальным напряжениям, надежна, если не выполняется – ненадежна. Перенапряжение не допускается.

II. Проектировочный расчет

Задано: нагрузка, длина и форма сечения балки, ее материал ([ ]) и нагрузка. Требуется: определить размеры сечения балки.

Определяются изгибающие моменты в сечениях балки (строятся эпюры М) и из условия прочности по в форме проектировочного расчета

W	max		M				(II)
ТР z

определяется требуемый момент сопротивления сечения ТРWz , по величине

которого из сортамента для стандартных сечений либо по формулам для нестандартных сечений определяют размеры сечений. Для прямоугольного сечения с целью обеспечения боковой устойчивости принимают в/h=5/7.

III. Определение допускаемой нагрузки

Задано: все размеры балки (Wz), материал ([ ]) и схема нагружения. Требуется: определить для балки допускаемую нагрузку.

Из условия прочности в форме определения допускаемого изгибающего

момента
	M Wz			(III)
определяем значение M , а	затем, согласно схеме нагружения, определяем
допускаемую нагрузку.
	Пример
	Из условия прочности		М = Wz.
	С другой стороны max		M	F l .

Подставляя в условие прочности, получим

F]l = Wz,

откуда

F Wz .

l

17

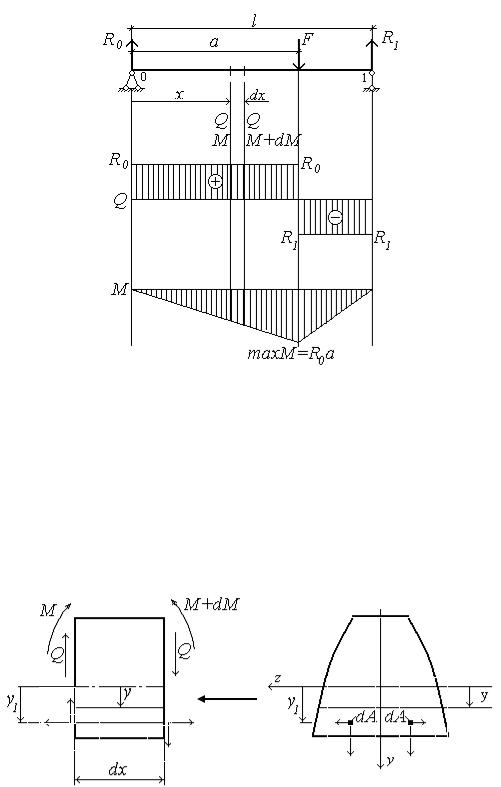
Касательные напряжения при ППИ. Формула Д.И.Журавского

При ППИ в сечении балки возникают как нормальные (), так и касательные () напряжения, равнодействующими которых являются изгибающий момент (М) и поперечная сила (Q), соответственно.

Рассмотрим простую балку в состоянии ППИ.

Выделим элемент балки длиной dx на расстоянии х от опоры 0. В левом сечении балки, согласно методу сечений, действуют положительные поперечная сила Q и изгибающий момент М, в правом сечении – поперечная сила Q и изгибающий момент М+dМ. В левом и правом сечениях на расстоянии у1 от главной центральной оси z выделим, симметрично относительно оси у, элементарные площадки с площадью dA и приложим к ним нормальные и касательные напряжения, соответствующие действующим внутренним усилиям. Также как и момент М, нормальные напряжения в правом сечении будут больше, чем в левом, на величину d.

Вид А

		y	А
				z	z
			+d
		y		y	y

Заметим, что наряду с касательными напряжениями у, в сечениях будут действовать также касательные напряжения z. Однако, у балок, сечения которых симметричны относительно оси у, что имеет место при ППИ, эти

18

напряжения малы и распределены по сечению симметрично относительно оси у (см. рис.), поэтому ими пренебрегают. Также заметим, что напряжения z играют существенную роль при расчете балок из тонкостенных несимметричных профилей.

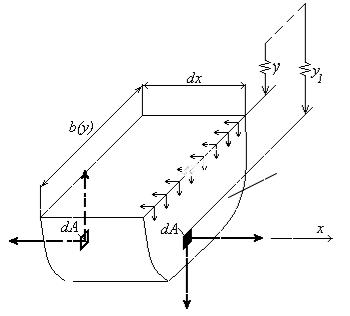
Определим напряжения y (индекс «у» у напряжений в дальнейшем будем опускать). Для этого плоскостью, параллельной нейтральному слою, расположенной от него на расстоянии у, рассечем элемент и рассмотрим равновесие нижней его части (см. рис.).

		А1
		+d

Согласно закону парности касательных напряжений, по площади горизонтального сечения, перпендикулярно ребру, будут действовать касательные напряжения, которые равны по величине касательным напряжениям , действующим в поперечном сечении на уровне у. Обозначим через А1 – площадь части поперечного сечения, расположенной ниже уровня горизонтального сечения (у).

Используем следующие допущения:

1)касательные напряжения равномерно распределены по ширине

сечения;

2)при определении будем пользоваться формулой для , полученной при чистом изгибе;

3)продольные волокна балки не надавливаются друг на друга ( y=0). Заметим, что по длине элемента dx напряжения также распределены

равномерно.

Запишем уравнение равновесия для проекций сил на ось х

X dA b( y)dx d dA 0 .

A1	A1
Здесь интегралы представляют собой	равнодействующие нормальных

напряжений , которые прикладываются по площади А1 левого и правого поперечных сечений. Приводя в полученном уравнении подобные члены, выразим искомые касательные напряжения. При этом внесем под знак

19

Szотс

интеграла длину элемента dx, как величину, не зависящую от переменной интегрирования. В результате получим

	1				d
							dA .		(9)
		b( y)			dx
				A
				1
Выполним в этом соотношении ряд преобразований и подстановок.
Представим интеграл в виде	d		dA			d		dA, куда подставим выражение для
A	dx			A		dx
1				1

нормальных напряжений, записанное согласно принятому допущению 2. В результате будем иметь

d

d M y

y dM

dA

dA

dA.

A

dx

A

dx

I z

A

I z

dx

1

1

1

Второе дифференциальное соотношение Журавского имеет вид dMdx Q , где Q

– поперечная сила в сечении. С учетом этого, рассматриваемый интеграл запишется в форме

	d				y
		dA				Q dA .
A	dx		A		I z
1			1

Вынесем за знак интеграла величины, которые не зависят от переменной интегрирования, и подставим полученное выражение в формулу (9)

Q

I z b( y) A y dA .

Здесь: y dA Szотс - статический момент относительно главной центральной

A1

оси z отсеченной части площади поперечного сечения А1. С учетом этого

формула для касательных		напряжений			при ППИ (формула
Д.И.Журавского) принимает вид
		Q S отс
		z			(10)
		I z b( y)

Напомним обозначения, входящие в формулу Журавского:

Q – поперечная сила в сечении, в котором определяются напряжения ; Iz – момент инерции поперечного сечения относительно оси z;

b(y) – ширина сечения на уровне, где определяется напряжения;

– статический момент относительно оси z части площади, которая лежит либо выше, либо ниже уровня, где определяются касательные напряжения (см. рис. ниже).

20