Modul-5_ppi

Последнее положение требует пояснения. Согласно теореме сложения, статический момент всего поперечного сечения относительно оси z равен

Sz Szв Szн , где Szв и Szн статические моменты верхней и нижней частей сечения относительно оси z.

С другой стороны, поскольку ось z является центральной, Sz 0 . Отсюда следует Szв Szн . В формулу Журавского подставляется абсолютная величина рассматриваемых статических моментов, т. е. Szотс Szв Szн , где

Szв АотсВ ycотсВ,

Szн АотсН ycотсН .

В этих формулах: АотсВ , АотсН - площади верхней и нижней частей сечения; ycотсВ , ycотсН - расстояния от оси z до центра тяжести верхней и нижней частей

сечения.

Отметим, что знак касательных напряжений, вычисляемых по формуле Журавского, определяется только знаком поперечной силы Q.

Эпюры касательных напряжений для некоторых сечений балок при ППИ

1. Прямоугольное сечение. Определим для балки прямоугольного сечения касательные напряжения в произвольной точке (на расстоянии у от оси z) заданного сечения и построим эпюру .

max 3Q

2A

Полагаем, что в заданном сечении Q0. Используя формулу Журавского, определим напряжения на уровне y. Для этого запишем соотношения для всех величин, входящих в формулу Журавского, через размеры прямоугольного сечения

21

bh3

; b( y) b ;

отс

отс

отс

отс

h

отс

h

1

I z

Sz

А

yc

;

А

y

b ;

yc

y

;

12

2

2

2

отс h

Sz

2

	h
y	b
		2

		1	h2			2			b
y					y					.
		2		4					2

Подставим эти соотношения в формулу (10), получим

h2

b

h2

Q

y 2

6Q

y2

4

2

4

;

либо

bh3

b

bh3

12

Из последней формулы видно, что по высоте сечения изменяется по закону квадратной параболы.

Строим эпюру по трем точкам:

1) на контуре при y h2 , имеем =0.

2) на оси при y=0:		6 Q h2			3Q	.
	max	4	b h3		2bh

Учитывая, что bh=A –площадь сечения, для прямоугольного сечения получаем:

	3Q		(11)
max	2A

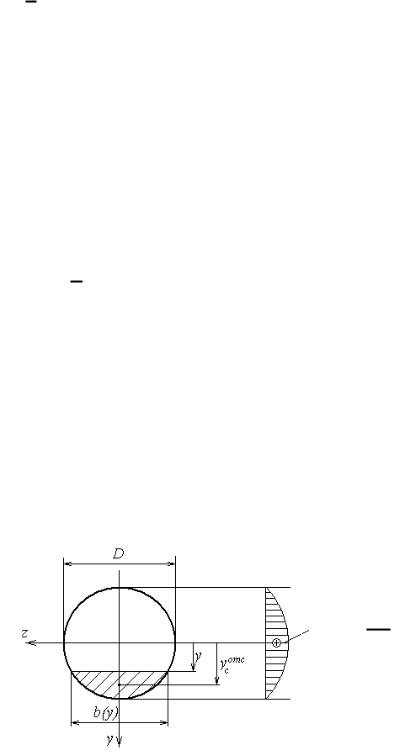
2. Круговое сечение. Эпюра для балки кругового сечения при Q 0 имеет такую же форму, но другое максимальное значение напряжений (см. рис.).

max 4Q

3A

3. Двутавровое сечение. Представим двутавровое сечение в виде трех прямоугольников. Для стенки двутавра эпюра строится так же, как и для прямоугольного сечения. Заметим, что для стандартного двутаврового сечения в сортаменте приводится статический момент полусечения (Sx либо maxS),

подстановка которого в формулу (10) Szотс =Sx=maxS , наряду с подстановкой

22

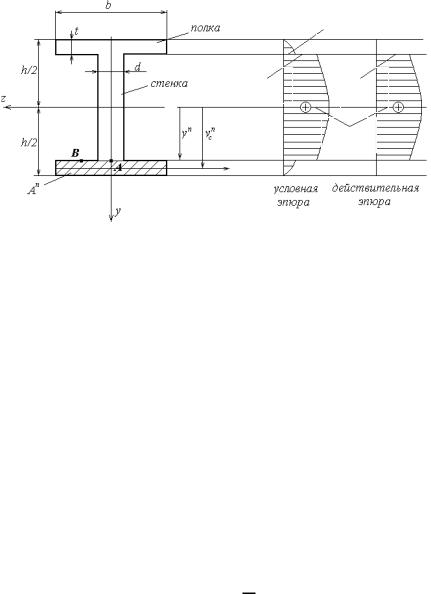
Iz= I xсорт и b(y)=d (эти величины берутся также из сортамента), дает максимальное значение напряжений в стенке двутавра (max). В случае рассматриваемого нестандартного сечения значения Iz и Szотс следует вычислять, как для сложного сечения, состоящего из трех прямоугольников.

Определим напряжения в точке К, лежащей на границе полки и стенки.

п

ст

ст

max

Заметим, что со стороны стенки b(y)=b, а со стороны полки – b(y)=d. Таким образом, напряжения на границе между стеной и полкой со стороны полки (п) и со стороны стенки (ст) будут соответственно равны

	n	Q S n		ст	Q S n
		z	,		z	.
		I z b
					I z d

Здесь: Szотс Szn - статический момент полки относительно оси z.

	Для		стандартного		профиля величина Szn определяется по формуле
S n	max	S S ст , где:		S ст	- статический момент полустенки (величины h, t, d
z			z	z

берутся из сортамента) Szст 0,5d(0,5h t)2 .

Для рассматриваемого нестандартного сечения Szп Ап yсп , где: площадь полки Ап=b t, расстояние от оси z до центра тяжести полки ycп 0,5(h t).

Сравнивая выражения для напряжений п и ст, получим

ст n db .

Заметим, что для стандартных профилей отношение b/d изменяется в пределах от 12 до 24, т.е. минимальные касательные напряжения, возникающие в стенках двутавровых балок, оказываются более чем на порядок выше максимальных касательных напряжений в полке. Кроме того, в точке В, лежащей на контуре полки на уровне точки К, отсутствует внешняя нагрузка, а следовательно отсутствуют и касательные напряжения ( = 0), Это указывает на неравномерность распределения по ширине полки, что противоречит допущению, положенному в основу вывода формулы Журавского. Таким образом, формула Журавского для определения в полке двутавра не

23

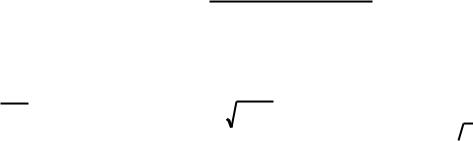
применима. В этой связи, а также учитывая, что п ст, касательными напряжениями в полках двутавра пренебрегают и строят для этого профиля, так называемую, действительную эпюру (только для стенки). На рисунке для случая Q0 приведены условная и действительная эпюры для балки двутаврового сечения при ППИ.

В общем случае формула Журавского применима для балок, сечение которых не имеет резких изменений по высоте.

Максимальные касательные напряжения в сечении, как правило, действуют в области оси z, однако есть исключения (сечения, вытянутые в области оси z по ширине).

Условие прочности при ППИ по касательным напряжениям

В общем случае условие прочности по касательным напряжениям имеет

вид

max .

(*)

Наибольшие по абсолютной величине напряжения возникают в наиболее напряженной точке – опасной точки в опасном сечении. При ППИ опасное сечение по касательным напряжениям – сечение, в котором Q=max Q , а опасная точка располагается, как правило, на оси (у0=0). В этой точке

отношение Szотс /b(y0) достигает максимального значения. Таким образом, касательные напряжения в наиболее напряженной точке будут равны

max

Q

max

Szотс

.

max

I z

b y0

Подставляя эти напряжения в выражение (*), получим условие прочности при

ППИ по касательным напряжениям

						Szотс
	max		Q
					max				.	(12)
	I	z				b y
				0

Здесь: - допускаемое значение касательного напряжения при сдвиге. Заметим, что при ППИ балка находится в плоском напряженном состоянии. Для пластичных материалов наиболее эффективна IV

энергетическая теория прочности, которая при плоском НС имеет вид:

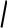x2 y2 x y 3 y2 .

При чистом сдвиге нормальные напряжения х=у=0, а у=. Тогда условие прочности принимает вид

3 2 , откуда 3 2 0,577 .

3

Округляя, принимаем

0,6 .

24

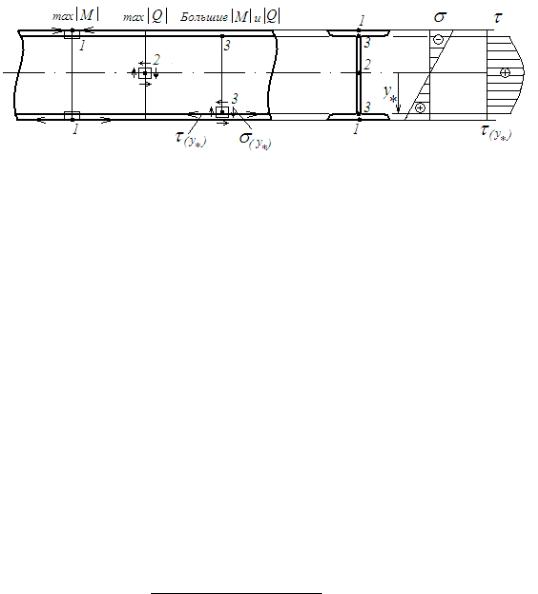
Полный расчет балки на прочность при ППИ

При ППИ наиболее напряженной точкой может быть одна из следующих трех точек:

1)точка 1, в которой =max (точка, опасная по нормальным напряжениям);

2)точка 2, в которой =max (точка, опасная по касательным напряжениям);

3)точка 3, в которой одновременно большими по абсолютной величине

оказываются напряжения и (точка, опасная по главным напряжениям). Ниже, на рисунке приведена балка, у которой выделены три опасных

сечения: по нормальным (М=maxМ ), касательным (Q=maxQ ) и главным (большие М и Q ) напряжениям, а также три указанных выше наиболее напряженных точки.

В соответствии с этим для балки при ППИ формулируется три условия прочности.

I. Условие прочности по (основное условие прочности при ППИ)

max

M

Опасное сечение – там, где М=maxМ.

Wz

(I)

Опасная точка – наиболее удаленная от оси.

II. Условие прочности по

Опасное сечение – там, где Q=maxQ.

max

Q

отс

max Sz

I z b( yоп )

(II)

Опасная точка – как правило, на оси.

III. Условие прочности по главным напряжениям

Как уже отмечалось, при ППИ балка находится в плоском НС, причем

х= , y=0, y= .

В случае стальных балок, изготовленных из пластичных материалов, для формулировки условия прочности используем IV энергетическую теорию прочности

2x 2y y x 32y .

25

С учетом приведенных выше соотношений, будем иметь

	.
2 32		(*)

Из эпюр и , представленных на рисунке, видно, что одновременно больших значений и достигают на границе между полкой и стенкой со стороны стенки при y=y* (точка 3). На уровне этой точки нормальные и касательные напряжения определяются по формулам

					Q			S п
( y ) M оп y			и ( y* )				оп	z	.
*
	*						I z d
	I z

Здесь: Szn – статический момент полки двутавра относительно оси z сечения; d

– толщина стенки двутавра.

Подставляя эти выражения в соотношение (*), получим условие

прочности для двутавровой балки по главным напряжениям

M

оп

2

Q

S п

2

y

3

оп

z

(III)

*

I z d

I z

Таким образом, опасное сечение по главным напряжениям будет там, где достигают одновременно больших значений по абсолютной величине поперечная сила Q и изгибающий момент М (тяготеет к большим значениям

М).

Опасная точка по главным напряжениям для двутавровой балки находится на границе между полкой и стенкой со стороны стенки.

В общем случае опасная точка по главным напряжениям располагается в месте резкого изменения ширины сечения со стороны меньшего размера. Если такой точки у сечения нет (прямоугольное, круговое сечение и т.д.) это условие прочности не используется.

Последовательность расчета балок на прочность при ППИ

1.Выполняется построение эпюр Q и М. и определяется положение опасных сечений.

2.Из условия прочности по в форме проектировочного расчета определяются размеры сечения балки (напомним, что из трех условий

прочности при ППИ условие прочности по является определяющим)

ТР Wz max M .

Wz

3. Проводится проверка принятой балки на прочность по касательным и главным напряжениям. Если какое-либо условие не выполняется, размеры сечения последовательно увеличивают до выполнения этого условия.

26

Некоторые рекомендации

1. При ППИ ориентировать сечение балки необходимо таким образом, чтобы плоскость ее максимальной жесткости совпадала с силовой плоскостью Напомним, что сечение балки вытянуто в плоскости ее максимальной жесткости.

2.Для балок, изготовленных из материалов, одинаково работающих на растяжение и сжатие, эффективны бисимметричные сечения. В этом случае максимальные растягивающие и сжимающие напряжения у балки будут одинаковы, что дает возможность максимально использовать материал балки.

3.Для балок, изготовленных из материала, который плохо сопротивляется растяжению (бетон, кирпич), эффективны сечения с одной осью симметрии, причем балки должны быть ориентированы таким образом, чтобы наибольших значений по абсолютной величине достигали напряжения сжатия. Материал балки в этом случае будет использован рационально.

4.При изгибе эффективными являются сечения, у которых материал разнесен как можно дальше от центра тяжести. Эти сечения обладают большими значениями удельного сопротивления

Wуд Wz3 .

A

Чем больше величина Wуд, тем рациональнее используется материал балки (в области больших нормальных напряжений располагаются большие массы материала). Примером такого сечения является двутавр.

ДЕФОРМАЦИИ БАЛОК ПРИ ППИ

Для обеспечения надежной работы балок необходимо, чтобы, наряду с

условиями прочности, выполнялось также условие жесткости
max v v .	(13)

Здесь: v – прогиб балки;

v - допускаемое значение прогиба.

27

1

Согласно СНиП, v

1000

1

l , где l – длина пролета, либо консоли.

250

Для проверки балки на жесткость, необходимо определять прогибы. Кроме того, прогибы необходимо уметь определять также при расчете на прочность статически неопределимых балок.

Дифференциальное уравнение упругой линии (изогнутой оси) балки

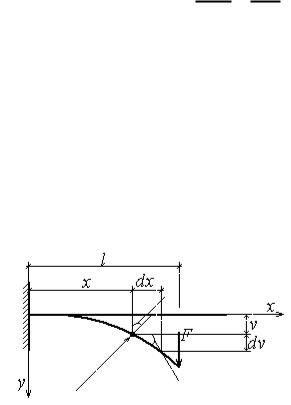
Рассмотрим деформацию консольной балки, нагруженной на свободном краю силой F.

Плоская кривая, форму которой приобретает ось балки при деформации ППИ, называется упругой линией балки (искривленной осью).

				– радиус кривизны оси
		балки
		1		– кривизна оси балки

При ППИ деформация оси балки полностью характеризует деформацию балки в целом. К характеристикам деформации балок относятся:

-прогиб балки ( ) – вертикальные смещения точек оси или, иначе, смещения точек оси, перпендикулярные к ее исходному положению. Поскольку мы рассматриваем малые перемещения, прогиб считаем также малым (горизонтальными или, иначе, продольными смещениями точек оси при этом пренебрегаем).

-угол поворота сечения ( ) – угол, на который разворачивается рассматриваемое сечение балки при деформации. Этот угол, согласно гипотезе Я.Бернулли, равен углу между касательной к упругой линии в заданном сечении и недеформированной осью.

Правило знаков для и :

-прогиб – положительный вниз (отрицательный вверх);

-угол поворота сечения – положительный по ходу часовой стрелки.

Связь между характеристиками деформаций балки

На расстоянии х от заделки выделим элемент оси балки длиной dx в исходном и деформированном состоянии (см. рис.). В сечении балки х погиб –, в сечении х+dx прогиб увеличился на величину d. Поскольку длина элемента мала, отрезок изогнутой оси заменим отрезком прямой, касательной к изогнутой оси в сечении х. Проведем от левого края деформированной оси балки до вертикальной прямой, соединяющей исходную и деформированную

28

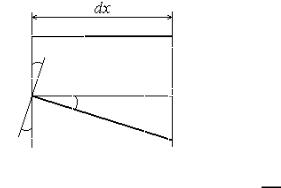
оси в сечении х+dx, горизонтальную прямую. Получили в результате прямоугольный треугольник с катетами dx и d.

d

Из рисунка видно, что tg dvdx . Поскольку прогибы малы, мал также и

	угол , что позволяет принять tg . Тогда
			dv		,	(14)
			dx

т.е. угол поворота сечения равен производной от прогиба по переменной х.

Уравнение упругой линии балки

Установим связь между характеристиками деформаций и внутренними усилиями, возникающими в сечении балки при ППИ. Предварительно отметим, что для рассматриваемых балок средней и большой длины (l5h) решающим фактором при определении деформаций является изгибающий момент М. Вклад поперечной силы Q при этом пренебрежимо мал, однако он увеличивается при уменьшении длины балки и для коротких балок должен учитываться в расчетах. Рассматриваем, как и ранее балки средней длины и длинные.

Напомним, что при выводе формулы для при чистом изгибе было получено соотношение между кривизной оси балки (1/ ) и изгибающим моментом в сечении (формула 5)

	1		M	,	(5)
			E I z

где E I z – изгибная жесткость балки.

В дифференциальной геометрии выражение для кривизны плоской кривой имеет вид:

				d 2v
1				dx2							(15)
								3
			dv				2		2
		1
			dx

Подставляя (15) в (5), получим связь между прогибом и изгибающим моментом

29

						3
d 2v		dv 2
						2		M
	1									.
dx2
		dx						EI	z

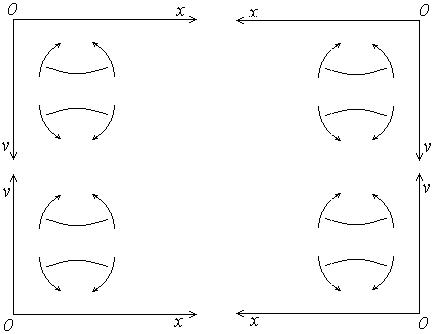
Знак в этой формуле определяется в зависимости от знака изгибающего момента и знака кривизны: если знаки момента и кривизны одинаковы – в формуле знак «+», если разные – знак «-». Заметим, что знак кривизны определяется используемой системой координат, знак же изгибающего момента от направления координатных осей не зависит, а определяется согласно характеру деформаций нижних и верхних волокон балки. В этой связи, ниже, в различных системах координат для участков балки с положительными и отрицательными изгибающими моментами приведены знаки кривизны оси

	M0;	1	0	M0;	1	0
	M0;	1	0	M0;	1	0

	M0;	1	0	M0;	1	0
	M0;	1	0	M0;	1	0

В системе координат, которую мы используем в расчетах (система 1), знаки моментов и кривизны для деформированных осей балок различны, поэтому в рассматриваемом уравнении принимаем знак «-»

						3
d 2v		dv 2
						2		M
	1									.	(16)
dx2
		dx						EI	z

Уравнение (16) является точным уравнением упругой линии балки. Это

дифференциальное уравнение второго порядка, обыкновенное, неоднородное,

нелинейное. Нелинейность приводит к определенным трудностям решения

такого уравнения. Однако, поскольку мы рассматриваем малые перемещения и

30