1.3. Предельные теоремы

Если монета бросается 100 раз подряд, то вероятность того, что

орёл выпадет 50 раз определяется по формуле биномиального распределения Однако вычислять столь большие величины как 100! затруднительно даже на вычислительной машине. Поэтому весьма важны предельные теоремы теории вероятностей.

Закон больших чисел.

Пусть Х₁,Х_2,…– независимые, одинаково распределённые сл.вел. с математическим ожиданием . Тогда их среднее арифметическое Y=стремится к с ростом n, т.е. для любого сколь угодно малого .

Р()

Согласно закону больших чисел число выпадения орла при 100- кратном бросании монеты будет ненамного отличаться в процентном отношении от 50.

Центральная предельная теорема.

Пусть Х₁, Х₂,…– независимые, одинаково распределённые сл.вел. с математическим ожиданием  и дисперсией ². Тогда сл.вел. будет иметь математическое ожиданиеи дисперсию. Приведём её к стандартному видуТогда согласно центральной предельной теореме в пределесл.вел.распределена по закону

С помощью центральной предельной теоремы можно найти, например, вероятность того, что при 100- кратном бросании монеты число выпадений орла Х будет заключено в интервале от 45 до 55. Сл.вел. Х есть сумма бернулиевских сл.вел. Х₁, Х₂, …, Х₁₀₀, каждая из которых равна 1 с вероятностью и 0 с вероятностью также. ПоэтомуЧисло 100 достаточно велико, чтобы считать, что величинараспределена по законуИмеем:

Здесь мы воспользовались чётностью функции из которой следует, чтоТеперь, обратившись к таблице функции ЛапласаФ(Х)= 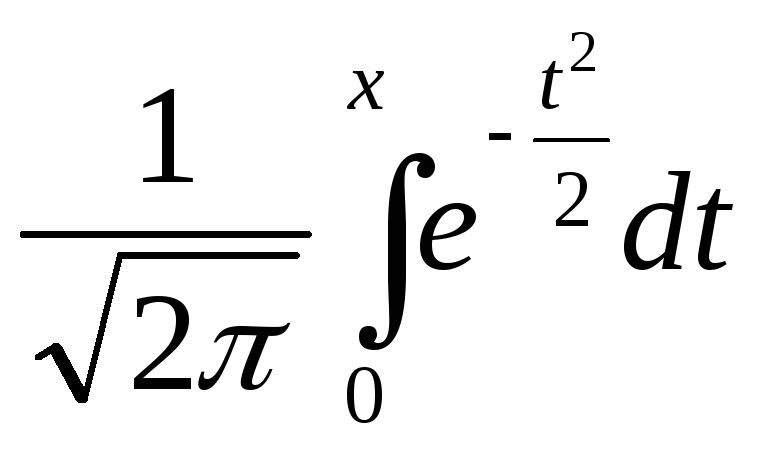, данной в Приложении, находим, чтоФ(1)=0,341 и искомая вероятность равна 0,682.

Пуассоновское приближение для биномиального распределения.

Пусть Х– биномиальная сл.вел.: Еслитак, чтоМХ= остаётся постоянным, то т.е. биномиальное распределение переходит в пуассоновское. Это позволяет приближённо вычислять биномиальные вероятности, когдаn велико, р мало, а их произведение nр не слишком малая и не слишком большая величина.

Пусть взято 100 семян, прорастающих с вероятностью 0,02. Какова вероятность, что хотя бы одно из семян прорастёт? (Р(А)=?).

Воспользуемся пуассоновским распределением с параметром

Р(А)=1-Р

1.4. Генеральная совокупность и выборка

Изучаемое множество, состоящее из большого числа объектов, называется в математической статистике генеральной совокупностью, а выбранное из него для изучения ограниченное число объектов- выборкой. Если объекты имеют некоторый числовой признак или характеристику, то случайный выбор объекта из генеральной совокупности порождает дискретную случайную величину. Число её значений заведомо не превышает объёма генеральной совокупности. При большом объёме генеральной совокупности, однако, такую случайную величину считают непрерывной и описывают функцией распределения, что значительно удобнее, чем хранить миллионы значений. Так, если генеральная совокупность- население страны, а числовой признак- возраст, то расстояние между соседними точками дискретного распределения составляет доли секунды и непрерывная модель вполне оправдана.

При таком подходе выборка (х₁, х₂,…, х_n) числовых значений признака из генеральной совокупности рассматривается как n независимых последовательных реализаций случайной величины Х. Выборочным средним называется среднее арифметическое элементов выборкиТак как элементы выборки– это случайные величины, то и выборочное среднее– случайная величина. ЕслиМХ=, DX=², то 1) М=, 2) Первое из этих равенств говорит о том, что выборочное среднее– несмещённая оценка математического ожидания, а второе- что точность этой оценки растёт с ростомn.

Выборочной дисперсией D_в называется величина Можно показать, чтот.е. выборочная дисперсия является смещённой оценкой дисперсии. Однако, её легко подправить так, чтобы получить несмещенную оценку.

Исправленной выборочной дисперсией называется величина

На практике разница между выборочной дисперсией и исправленной выборочной дисперсией существенна лишь при небольшом объёме выборки.

Если в выборке объёма n есть повторяющиеся значения, так что всего имеется k<n различных значений, то её удобно задать таблицей частот значений

х1	х2	…	хк
n1	n2	…	nк

при этом сумма частот равна объёму выборки: n₁+ n₂+…+ n_к= n.

В этом случае формулы для выборочного среднего и выборочной дисперсии запишутся в виде:

В медицине и биологии при изучении воздействия на живые организмы различных препаратов, а также в вопросах, связанных с маркетингом, возникает задача о сравнении средних двух генеральных совокупностей. Пусть имеется 2 распределения Х и Y: МХ=_х, DX=_х², МY=_у, DY=_у². С целью проверки равенства _х=_у из них извлечены выборки объёмов соответственно n и m, найдены средние и и исправленные выборочные дисперсиииЕсли_х=_у и объёмы выборок достаточно велики (не менее 30 каждая), то, опираясь на центральную предельную теорему, можно считать, что величина

распределена по закону (0,1). Поэтому, если  оказывается большим по абсолютной величине, то мы склонны отбросить гипотезу о равенстве математических ожиданий. Сформулируем точное правило.

Пусть взято малое положительное число , 01, которое в дальнейшем будем называть уровнем значимости. По таблице нормального распределения найдём _кр такое, что . Теперь, если абсолютное значение величины, то гипотезу о равенстве математических ожиданий отвергаем. Обычно полагаетсяпри этом _кр=1,95.

Рассмотрим пример. Пусть две выборки, объёмом 30 каждая, заданы таблицей частот:

	0	1	2	3
х	5	10	10	5
у	5	5	10	10

,

,

,

,

Так как _кр(0,05)=1,95 и 1,241,95, то при уровне значимости 0,05 нет оснований отвергать гипотезу о равенстве математических ожиданийМХ=МY.