
- •Роман Собкович, Наталія Кульчицька Основні методи доведення нерівностей
- •2014 Зміст
- •1.1. Доведення нерівностей за допомогою означення
- •1.2. Синтетичний метод доведення нерівностей
- •1.3. Аналітичний метод доведення нерівностей
- •1.4. Доведення нерівностей методом від супротивного
- •1.5. Метод підсилення при доведенні нерівностей.
- •1.6. Доведення нерівностей методом математичної індукції
- •1.7. Класичні нерівності між середніми та їх доведення
- •1.8. Наслідки з нерівності Коші та задачі на відшукання найбільших та найменших значень
- •2.1. Оцінка областей визначення та множини значень. Монотонність. Опуклість
- •2.2. Застосування властивостей квадратного тричлена
- •2.3. Застосування похідної
- •2.4. Застосування інтеграла.
- •2.5. Опуклі функції та їх застосування до доведення нерівностей. Нерівність Єнсена
- •2.6. Нерівність Юнга
2.4. Застосування інтеграла.
Використання інтегрального числення
при доведенні нерівностей використовує
наступні міркування. Нехай на проміжку
![]() задані дві неперервні функції
задані дві неперервні функції![]() та
та![]() і в усіх точках цього проміжку виконується
нерівність
і в усіх точках цього проміжку виконується
нерівність![]()
![]() .
Тоді на заданому відрізку виконується
також нерівність
.
Тоді на заданому відрізку виконується
також нерівність![]() .
Аналогічне твердження стосується також
випадків
.
Аналогічне твердження стосується також
випадків![]()
![]() ,
,![]()
![]() та
та![]()
![]() .
.
Алгоритм використання даного прийому
може виглядати наступним чином. Для
доведення нерівності
![]()
![]() розглядаємо функції
розглядаємо функції![]() та
та![]() ,
де
,
де![]() ,
,![]() .
Якщо виконується нерівність
.
Якщо виконується нерівність![]()
![]() ,
то стверджуємо, що вірна нерівність
,
то стверджуємо, що вірна нерівність![]() .
.
Задача 2.4.1. Довести, що при![]() виконуються нерівності
виконуються нерівності
![]() ,
,![]() .
.
Розв’язання. Оскільки на вказаному
проміжку виконується нерівність![]() ,
то
,
то![]() .
Звідси знаходимо
.
Звідси знаходимо![]() .
Інтегруючи одержану нерівність ще раз,
маємо
.
Інтегруючи одержану нерівність ще раз,
маємо
![]() .
.
З одержаної нерівності отримуємо, що
![]() .
.
Задача 2.4.2.Довести нерівність
![]() .
.
Розв’язання.Розглянемо функцію![]() ,
значення якої наявні в нерівності.
Оскільки кожний доданок
,
значення якої наявні в нерівності.
Оскільки кожний доданок![]() можна трактувати, як площу прямокутника
з висотою
можна трактувати, як площу прямокутника
з висотою![]() та основою, що дорівнює 1 (відстань між
точками
та основою, що дорівнює 1 (відстань між
точками![]() та
та![]() ),
то
),
то
![]() .
.
2.5. Опуклі функції та їх застосування до доведення нерівностей. Нерівність Єнсена
Розглянемо функцію
![]() ,
визначену та диференційовану на відрізку
,
визначену та диференційовану на відрізку![]() і позначимо через
і позначимо через![]() частину її графіка, що відповідає
відрізку
частину її графіка, що відповідає
відрізку![]() .
.
Ф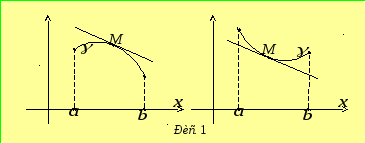 ункцію
ункцію![]() називають опуклою вгору (вниз) на відрізку
називають опуклою вгору (вниз) на відрізку![]() ,
якщо для довільної точки
,
якщо для довільної точки![]() крива
крива![]() лежить нижче (вище) від дотичної до
лежить нижче (вище) від дотичної до![]() ,
проведеної в точці
,
проведеної в точці![]() (рис. 1).
(рис. 1).
Серед деяких властивостей опуклих функцій відмітимо ті, які в подальшому використаємо при доведенні деяких нерівностей.
1. Якщо функція
![]() на відрізку
на відрізку![]() опукла вгору, то для двох довільних
різних точок
опукла вгору, то для двох довільних
різних точок![]() виконується нерівність
виконується нерівність
![]() .
.
2. Якщо функція
![]() на відрізку
на відрізку![]() опукла вниз, то для двох довільних різних
точок
опукла вниз, то для двох довільних різних
точок![]() виконується нерівність
виконується нерівність
![]() .
.
Д оведення
обох тверджень очевидне. Зокрема у
першому випадку достатньо побачити, що
довжина відрізка
оведення
обох тверджень очевидне. Зокрема у
першому випадку достатньо побачити, що
довжина відрізка![]() ,
який дорівнює
,
який дорівнює![]() ,
менша від довжини відрізка
,
менша від довжини відрізка![]() ,
який дорівнює
,
який дорівнює![]() (рис. 2).
(рис. 2).
3. Якщо функція
![]() на відрізку
на відрізку![]() опукла вгору і числа
опукла вгору і числа![]() не всі рівні між собою, то виконується
нерівність
не всі рівні між собою, то виконується
нерівність
![]() .
(*)
.
(*)
4. Якщо функція
![]() на відрізку
на відрізку![]() опукла вниз і числа
опукла вниз і числа![]() не всі рівні між собою, то виконується
нерівність
не всі рівні між собою, то виконується
нерівність
![]() .
(**)
.
(**)
Доведення двох останніх тверджень можна реалізувати за допомогою методу математичної індукції.
Нерівності (*), (**), які у математиці
називають нерівностями Єнсена, можуть
служити основою для складання та
доведення різних нерівностей. Достатньо
вибрати конкретну функцію, опуклу вгору
або вниз та замінити нею функцію
![]() .
.
Наведемо приклади подібних доведень.
Задача 2.5.1. Довести, що для різних![]() виконується нерівність
виконується нерівність
![]() .
.
Доведення. Для доведення достатньо
у співвідношенні (*) використати замість![]() функцію
функцію![]() ,
графік якої на вказаному відрізку
опуклий вверх.
,
графік якої на вказаному відрізку
опуклий вверх.
Задача 2.5.2.Довести, що для
довільних чисел![]() виконується нерівність
виконується нерівність
![]() .
.
Доведення. Тут ми повертаємося до
розгляду задачі 1.3.2. У цьому випадку
використовуємо співвідношення (**), а в
ролі![]() функцію
функцію![]() ,
графік якої при
,
графік якої при![]() опуклий вниз.
опуклий вниз.
Задача 2.5.3. Порівняти числа![]() та
та![]() .
.
Доведення. Розглянемо функцію![]() ,
графік якої на проміжку
,
графік якої на проміжку![]() опуклий вниз. Застосувавши нерівність
Єнсена у виді співвідношення (**), отримуємо
опуклий вниз. Застосувавши нерівність
Єнсена у виді співвідношення (**), отримуємо
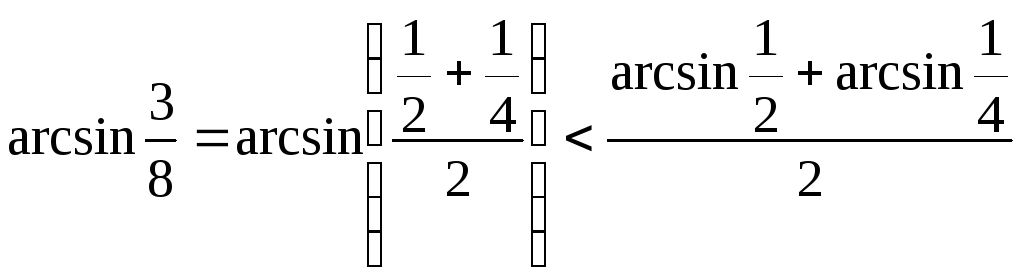 .
.
Тому
![]()
![]() .
.
Задача 2.5.4. Довести, що правильний![]() -кутник
має найбільший периметр серед усіх
вписаних в коло
-кутник
має найбільший периметр серед усіх
вписаних в коло![]() -кутників.
-кутників.
Доведення. Нехай![]() -кутник
-кутник![]() вписаний у коло з центром у точці
вписаний у коло з центром у точці![]() та радіусом
та радіусом![]() .
Позначимо
.
Позначимо![]() .
Тоді
.
Тоді![]() (знак строгої нерівності буде у випадку,
коли центр кола лежить поза многокутником).
Користуючись теоремою косинусів
отримуємо, що для периметра многокутника
(знак строгої нерівності буде у випадку,
коли центр кола лежить поза многокутником).
Користуючись теоремою косинусів
отримуємо, що для периметра многокутника![]() маємо
маємо
![]() .
.
Оскільки
![]() і функція
і функція![]() на вказаній множині значень опукла
вгору, то з нерівності Єнсена отримуємо,
що
на вказаній множині значень опукла
вгору, то з нерівності Єнсена отримуємо,
що
 ,
,
а саме останньому значенню дорівнює периметр правильного вписаного в коло многокутника.
Розглянемо, як нерівність Єнсена та
наведені міркування можна використати
для доведення класичних нерівностей
між середніми. Як ми уже знаємо (розділ
1.7), для
![]() додатних чисел
додатних чисел![]() такими є середнє арифметичне
такими є середнє арифметичне![]() ,
середнє геометричне
,
середнє геометричне![]() ,
середнє квадратичне
,
середнє квадратичне![]() та середнє гармонічне
та середнє гармонічне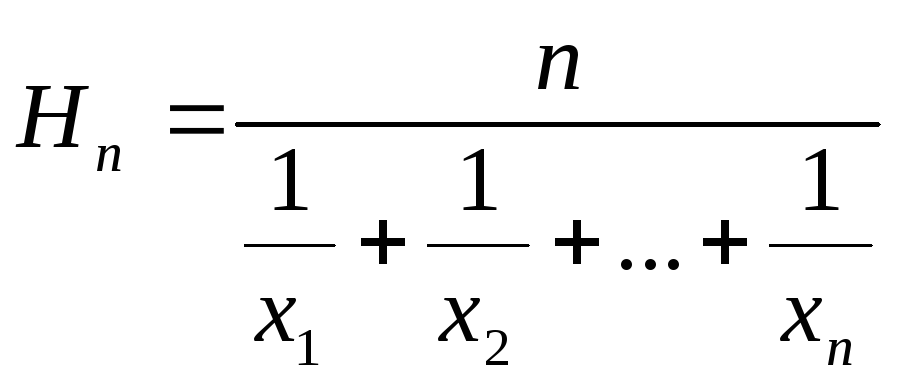 .
Ці середні величини знаходяться у
співвідношеннях
.
Ці середні величини знаходяться у
співвідношеннях![]() .
Знак рівності в усіх випадках виконується
тоді і тільки тоді, коли
.
Знак рівності в усіх випадках виконується
тоді і тільки тоді, коли![]() рівні. Доведемо строгі нерівності,
вважаючи
рівні. Доведемо строгі нерівності,
вважаючи![]() різними.
різними.
Для доведення першої нерівності
![]() ,
тобто
,
тобто
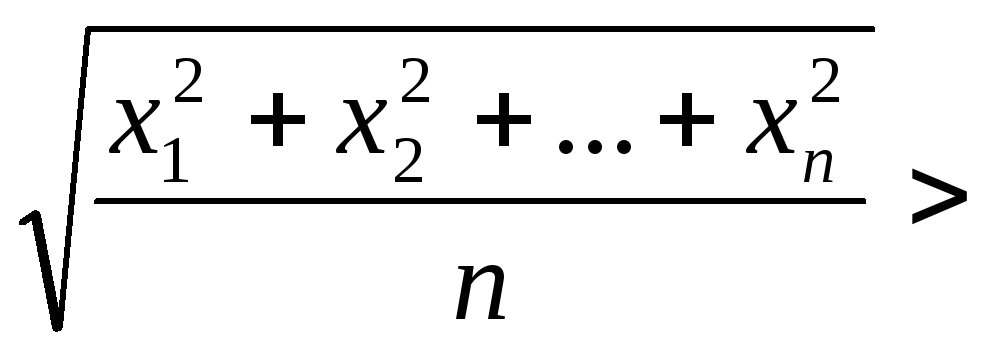
![]()
використаємо у ролі
![]() функцію
функцію![]() ,
графік якої опуклий вниз, та співвідношення
(**). Відповідно до нього отримуємо
,
графік якої опуклий вниз, та співвідношення
(**). Відповідно до нього отримуємо
![]() ,
,
звідки, добувши корінь з обох частин, дістаємо шукане співвідношення.
Для доведення другої нерівності
![]() ,
тобто
,
тобто
![]()
![]()
використаємо у ролі
![]() функцію
функцію![]() ,
графік якої опуклий вгору, та співвідношення
(*). Отримуємо
,
графік якої опуклий вгору, та співвідношення
(*). Отримуємо
![]()
або
![]() .
.
Потенціюючи одержаний вираз, отримуємо шукане співвідношення.
Для доведення останньої нерівності
![]() ,
тобто нерівності між середнім геометричним
та середнім гармонічним
,
тобто нерівності між середнім геометричним
та середнім гармонічним
![]()
 ,
,
знову використаємо функцію
![]() ,
тільки співвідношення (*) застосуємо до
чисел
,
тільки співвідношення (*) застосуємо до
чисел![]() .
Отримуємо
.
Отримуємо
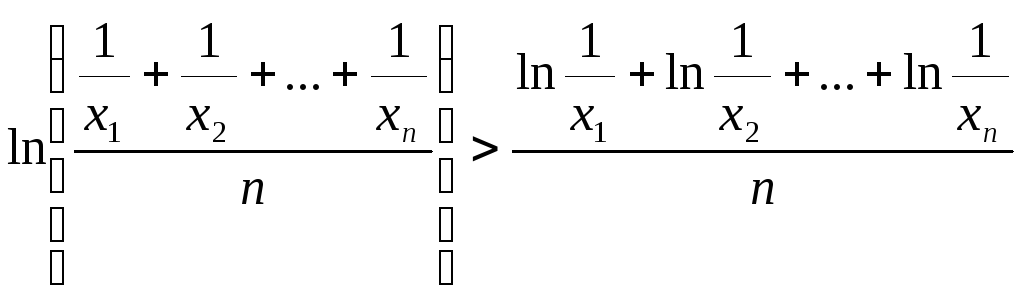
або
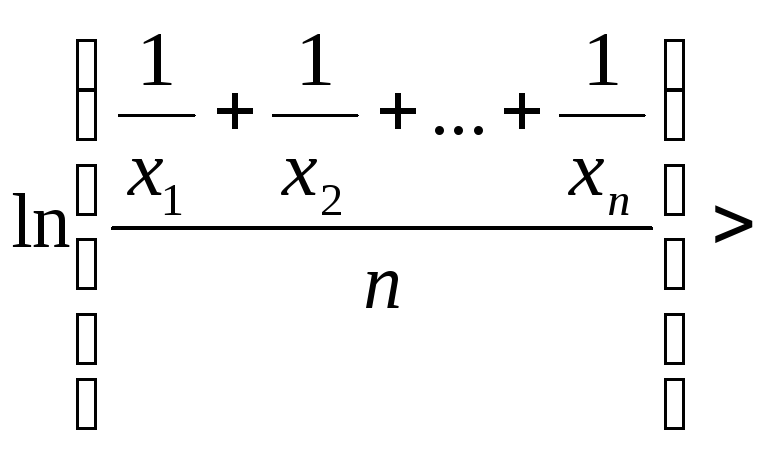
![]() ,
,
що фактично завершує доведення потрібної нерівності.
