
- •Роман Собкович, Наталія Кульчицька Основні методи доведення нерівностей
- •2014 Зміст
- •1.1. Доведення нерівностей за допомогою означення
- •1.2. Синтетичний метод доведення нерівностей
- •1.3. Аналітичний метод доведення нерівностей
- •1.4. Доведення нерівностей методом від супротивного
- •1.5. Метод підсилення при доведенні нерівностей.
- •1.6. Доведення нерівностей методом математичної індукції
- •1.7. Класичні нерівності між середніми та їх доведення
- •1.8. Наслідки з нерівності Коші та задачі на відшукання найбільших та найменших значень
- •2.1. Оцінка областей визначення та множини значень. Монотонність. Опуклість
- •2.2. Застосування властивостей квадратного тричлена
- •2.3. Застосування похідної
- •2.4. Застосування інтеграла.
- •2.5. Опуклі функції та їх застосування до доведення нерівностей. Нерівність Єнсена
- •2.6. Нерівність Юнга
2.2. Застосування властивостей квадратного тричлена
Ідея прийому доведень із застосуванням властивостей квадратного тричлена, полягає в наступному. Нехай у випадку, коли у нерівності наявний квадратний тричлен відносно деякої змінної, встановлено, що він не має коренів. Тоді при умові додатності старшого коефіцієнта потрібно, щоб дискримінант цього тричлена був від’ємним.
Навпаки, якщо нам вдається показати, що корені є, то цим самим ми фактично обґрунтовуємо, що дискримінант квадратного тричлена не може бути від’ємним. Іноді питання наявності коренів може виявитися дещо складнішим і тоді можна пробувати з’ясовувати, чи існують значення змінних, при яких вираз приймає значення різних знаків. Цього у випадку неперервності функції було б достатньо, щоб стверджувати факт наявності коренів.
Наведемо приклади задач.
Задача2.2.1. Якщо![]() ,
то
,
то![]() .
Довести.
.
Довести.
Доведення. Якщо![]() ,
то нерівність очевидна. Нехай
,
то нерівність очевидна. Нехай![]() .
Зведемо нерівність до виду
.
Зведемо нерівність до виду![]() та розглянемо квадратне рівняння
та розглянемо квадратне рівняння![]() .
Очевидно, що рівняння має корені (зокрема
коренем є значення
.
Очевидно, що рівняння має корені (зокрема
коренем є значення![]() ).
Тому дискримінант
).
Тому дискримінант![]() рівняння задовольняє умову
рівняння задовольняє умову![]() ,
звідки отримуємо потрібну нерівність
,
звідки отримуємо потрібну нерівність![]() .
Рівність можлива при рівних значеннях
всіх змінних.
.
Рівність можлива при рівних значеннях
всіх змінних.
Задача2.2.2. Для невід’ємних
чисел![]() довести нерівність
довести нерівність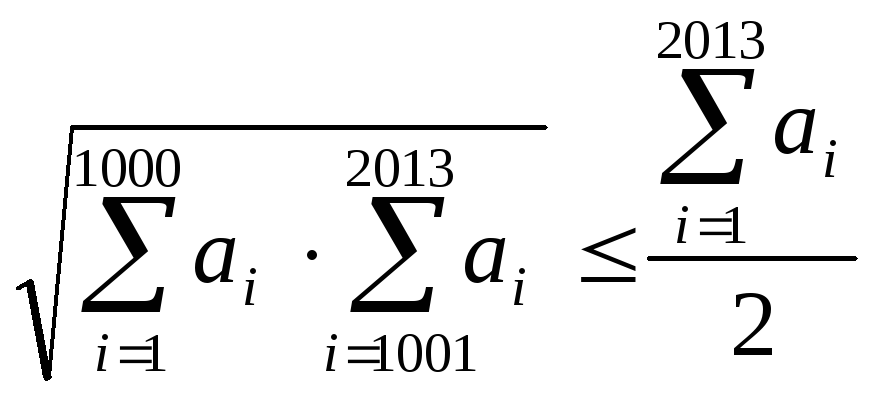 .
.
Доведення.Нехай![]() .
Запишемо нерівність у виді
.
Запишемо нерівність у виді
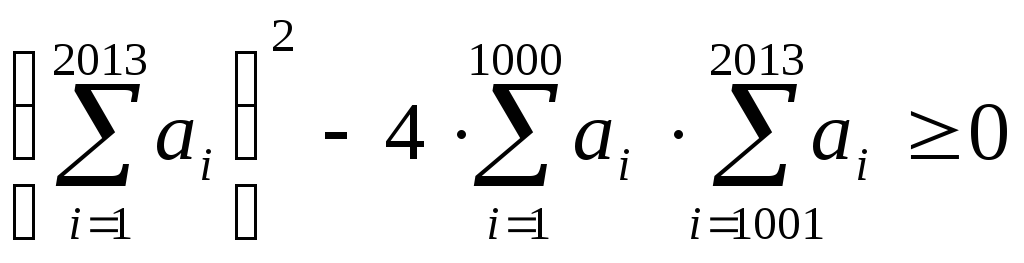
та розглянемо квадратне рівняння
![]() .
Очевидно, що рівняння має корені (зокрема
коренем рівняння є значення
.
Очевидно, що рівняння має корені (зокрема
коренем рівняння є значення![]() ).
Тому дискримінант
).
Тому дискримінант![]() рівняння задовольняє умову
рівняння задовольняє умову .
Звідси отримуємо потрібну нерівність.
Рівність можлива при рівних значеннях
всіх змінних.
.
Звідси отримуємо потрібну нерівність.
Рівність можлива при рівних значеннях
всіх змінних.
Задача 2.2.3.Довести, що при всіх![]() виконується нерівність
виконується нерівність
![]() .
.
Розв’язання. Розглянемо квадратний тричлен
![]() .
.
Знайдемо його значення в точках
![]() та
та![]() .
Маємо:
.
Маємо:
![]() ,
,
![]() .
.
Тепер, оскільки при
![]()
![]() ,
,
то можна стверджувати, що в точках
![]() та
та![]() функція приймає значення різні за
знаком. Тому на відповідному проміжку
існує корінь квадратного тричлена.
Отже, його дискримінант
функція приймає значення різні за
знаком. Тому на відповідному проміжку
існує корінь квадратного тричлена.
Отже, його дискримінант![]() додатний, а це доводить задану нерівність.
додатний, а це доводить задану нерівність.
При
![]() нерівність набуває виду
нерівність набуває виду![]() або
або![]() .
Записавши її у виді
.
Записавши її у виді![]() ,
бачимо, що при
,
бачимо, що при![]() вона вірна.
вона вірна.
Задача 2.2.4. Довести, що для всіх
дійсних значень![]() виконується нерівність
виконується нерівність![]() .
.
Розв’язання. Різницю![]() можна вважати дискримінантом квадратного
тричлена
можна вважати дискримінантом квадратного
тричлена![]() .
Даний тричлен має корені
.
Даний тричлен має корені![]() та
та![]() ,
тому його дискримінант не може бути
від’ємним. Знак рівності
можливий, коли ці корені рівні, тобто
при
,
тому його дискримінант не може бути
від’ємним. Знак рівності
можливий, коли ці корені рівні, тобто
при![]() або
або![]() .
.
Задача 2.2.5.Відомо, що один із
коренів рівняння![]() більший 2. Довести, що
більший 2. Довести, що![]() .
.
Доведення.Нехай![]() - корінь, про який іде мова в умові, тобто
- корінь, про який іде мова в умові, тобто![]() .
Маємо
.
Маємо![]() ,
,![]() .
Звідси
.
Звідси![]() або
або![]() .
.
Задача 2.2.6.Числа![]() такі, що
такі, що![]() .
Довести, що
.
Довести, що![]() .
.
Доведення.При![]() отримуємо нерівність
отримуємо нерівність![]() ,
яка не виконується тільки у випадку,
коли
,
яка не виконується тільки у випадку,
коли![]() .
Але тоді відповідно до умови матимемо
.
Але тоді відповідно до умови матимемо![]() ,
що неможливо. Отже,
,
що неможливо. Отже,![]() і нерівність при
і нерівність при![]() виконується.
виконується.
Нехай
![]() .
Розглянемо функцію
.
Розглянемо функцію![]() .
Оскільки
.
Оскільки![]() і
і![]() ,
то відповідно до умови отримуємо
,
то відповідно до умови отримуємо![]() .
Це означає, що на інтервалі
.
Це означає, що на інтервалі![]() знаходиться один із коренів квадратного
тричлена, тому його дискримінант
знаходиться один із коренів квадратного
тричлена, тому його дискримінант![]() .
.
Задача 2.2.7.Додатні числа![]() такі, що
такі, що![]() ,
,![]() .
Довести, що
.
Довести, що![]() .
.
Доведення. Короткий аналіз структури нерівності, яку потрібно довести, показує, що вираз
![]()
можна розглядати, як дискримінант квадратного тричлена
![]() .
.
Якщо ми зуміємо показати, що цей тричлен
приймає тільки додатні значення, то цим
самим доведемо, що
![]() .
Відповідно до умови квадратні тричлени
.
Відповідно до умови квадратні тричлени![]() та
та![]() такі, що при довільному
такі, що при довільному![]() виконуються нерівності
виконуються нерівності![]() ,
,![]() .
Очевидна також нерівність
.
Очевидна також нерівність![]() .
Додавши три одержані співвідношення,
отримаємо нерівність, яку доводимо.
.
Додавши три одержані співвідношення,
отримаємо нерівність, яку доводимо.
Задача 2.2.8.При яких значеннях
параметра![]() сума квадратів коренів рівняння
сума квадратів коренів рівняння![]() буде найменшою?
буде найменшою?
Розв’язання. Нехай![]() та
та![]() - корені заданого рівняння. За теоремою
Вієта маємо
- корені заданого рівняння. За теоремою
Вієта маємо![]() .
Тому
.
Тому
![]() .
.
Найменше значення одержаного виразу
дорівнює 1 і досягається воно при
![]() .
Залишається зауважити, що при
.
Залишається зауважити, що при![]() дійсні корені рівняння існують. Без
цієї перевірки вважати розв’язання
задачі завершеним не можна. Наприклад,
для аналогічної задачі з рівнянням
дійсні корені рівняння існують. Без
цієї перевірки вважати розв’язання
задачі завершеним не можна. Наприклад,
для аналогічної задачі з рівнянням![]() подібні міркування у вигляді перетворень
подібні міркування у вигляді перетворень
![]()
привели б до неправильної відповіді
![]() .
При цьому значенні
.
При цьому значенні![]() рівняння дійсних коренів не має.
рівняння дійсних коренів не має.
Задача 2.2.9.Довести, що для
будь-яких дійсних чисел![]() та
та![]() виконується нерівність
виконується нерівність![]() .
.
Доведення. Перетворимо заданий вираз наступним чином:
![]() .
.
Очевидно, що одержаний вираз не може
бути від’ємним, а значення
0 досягається при виконанні умов![]() ,
тобто при
,
тобто при![]() .
.
Даний результат можна було отримати і
за допомогою інших міркувань, зокрема
досліджуючи дискримінант лівої частини
нерівності, розглядаючи її, як квадратну
відносно змінної
![]() або
або![]() .
.
Задача 2.2.10. Довести нерівність![]() .
.
Доведення. Зробимо наступні перетворення:
![]() .
.
Отриманий вираз не може бути від’ємним,
а це доводить вказане в умові твердження.
Рівність можлива при![]() .
Цей самий результат випливає з того, що
дискримінант квадратного тричлена
.
Цей самий результат випливає з того, що
дискримінант квадратного тричлена![]() відносно змінної
відносно змінної![]() ,
який дорівнює
,
який дорівнює![]() ,
не може бути додатним.
,
не може бути додатним.
Задача 2.2.11. Довести нерівність![]() (приклад 1.2.6).
(приклад 1.2.6).
Доведення. Дискримінант квадратного
тричлена![]() відносно змінної
відносно змінної![]() ,
який дорівнює
,
який дорівнює![]() ,
не може бути додатним. Це означає, що
даний вираз не може приймати від’ємні
значення. Знак рівності досягається
при
,
не може бути додатним. Це означає, що
даний вираз не може приймати від’ємні
значення. Знак рівності досягається
при![]() .
.
Задача 2.2.12. Довести, що при
довільному дійсному![]() виконується нерівність
виконується нерівність
![]() .
.
Доведення. Перетворимо нерівність до виду
![]()
та розглянемо її ліву частину, як
квадратний тричлен відносно
![]() .
Дискримінант цього квадратного тричлена
.
Дискримінант цього квадратного тричлена![]() .
Оскільки
.
Оскільки![]() ,
то
,
то![]() .
Тому вираз
.
Тому вираз![]() не може приймати від’ємні
значення, що завершує доведення
нерівності. Знак рівності досягається
при
не може приймати від’ємні
значення, що завершує доведення
нерівності. Знак рівності досягається
при![]() .
.
Зауважимо, що в результаті нами одночасно отримано розв’язки відповідних тригонометричних рівняння та нерівності.
