1.8. Наслідки з нерівності Коші та задачі на відшукання найбільших та найменших значень

Повернемося до нерівності , де. Як було зауважено вище, знак рівності тут виконується тоді і тільки тоді, коли всі значеннярівні. Звідси можна отримати два цікавих факти, які мають ряд застосувань.

1. Якщо добуток є сталою величиною, то сумаприймає найменше значення. Прице значення дорівнює.

2. Якщо сума є сталою величиною, то добутокприймає найбільше значення. Привоно дорівнює.

Наведені міркування дозволяють доводити окремі нерівності з новими постановками задач.

Задача 1.8.1.Знайти найбільше і найменше значення функції

.

Розв’язання.Нехай,. Оскільки, то

.

Значення функції буде найменшим, коли найбільшим буде значення добутку .

Оскільки , то найбільше значенняпотрібно шукати при. Із нерівності Коші маємо. Але, тому. Найбільше значенняприйматиме при. Тоді:і найменше значення функції буде.

Найменше значення очевидно буде при. Примаємо,. Враховуючи ці значення, бачимо, що добуток буде мінімальним, оскількиприймає мінімальне значення, а-максимальне. Отже, прифункція приймає найбільше значення

.

Таким чином, найбільшим значенням буде а найменшим.

Задача 1.8.3.Знайти найбільше значення виразу, якщо.

Розв’язання. Згідно з умовою вираз(а, отже, і) прийматиме найбільше значення при=, тобто при. При цьому.

Задача 1.8.4.Знайти найменше значення виразу, якщо.

Розв’язання. Оскільки добуток виразівтає сталим (із умови випливає, що), то вираз прийматиме найменше значення при=, тобто при. При цьому, звідки.

Задача 1.8.5.Знайти найбільше значення функції.

Розв’язання.Призначення функції дорівнює 0. Призапишемо вираз для функції у виді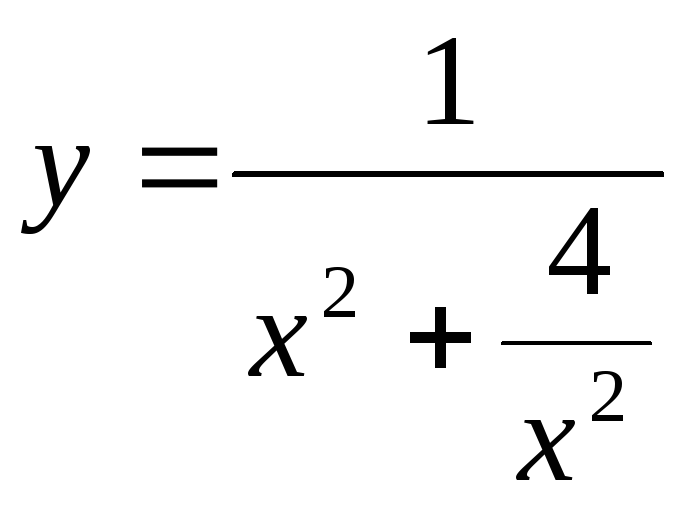. Дослідимо, коли знаменник виразу найменший. Зауваживши, що добуток виразівтає сталим числом, робимо висновок, що знаменник найменший при, тобто при. Значення функції при цьому є максимальним і буде дорівнювати.

Задача 1.8.6.Довести, що для довільних чиселвиконується нерівність

.

Доведення. Ми уже розглядали доведення даної нерівності, використовуючи нерівність Коші. Зупинимося на інших міркуваннях. Оскільки добуток чиселє сталою величиною, то їхня сума буде

.

Задача 1.8.7. Оцінити значення виразу.

Розв’язання.Нехай,. Тоді

і сума прийматиме найменше значення, коли добуток найбільший. Оскільки виразє сталим, то максимальне значення буде при, тобто, колиабо при. Значення заданого виразу у цьому випадку дорівнює. Одержали нижню оцінку виразу. Верхня оцінка випливає з нерівностей. Рівність досягається у точках.

Таким чином, .

Розділ 2. Застосування властивостей функцій при доведенні нерівностей

2.1. Оцінка областей визначення та множини значень. Монотонність. Опуклість

При доведенні нерівностей в окремих випадках доцільно проаналізувати область визначення та множину значень заданих в умові виразів. Цього іноді може виявитися достатньо для розв’язання задачі.

Задача2.1.1.Довести нерівність

.

Доведення. Нема потреби робити певні перетворення при доведенні даної нерівності. Достатньо, порівнюючи підкореневі вирази, побачити, що при довільнихтавиконується нерівність. Тому ліва частина приймає значення менші, ніж права.

Задача2.1.2.Придовести нерівність

.

Доведення. Очевидно, що

,,.

Тому ліва частина виразу приймає значення більші або рівні 1. Отже, нерівність виконується на всій області допустимих значень, тобто при . Знак рівності досягається при.

Задача2.1.3.Довести нерівність

.

Доведення. Проаналізуємо область визначення виразу. Для його лівої частини вона визначається системою нерівностей

з єдиним розв’язком . При знайденому значенні ліва частина нерівності набуває значення 2. Залишається зауважити, що в правій частині нерівності є сума двох обернених чисел, яка не менша 2. Знак рівності досягається при.

Задача 2.1.4.Довести нерівність

.

Доведення. Насамперед зауважимо, що ліва частина нерівності визначена на проміжкуі, монотонно зростаючи на цьому проміжку, приймає найменше значення у точці. Це значення дорівнює 2. Записавши праву частину нерівності у виді, бачимо, що значення цього виразу не перевищують 2, причому рівність двом досягається в єдиній точці. Порівнюючи множини значень обох частин заданого виразу, робимо висновок, що рівність можлива тільки при. Для інших значень змінних нерівність буде строгою.

Задача 2.1.5.Довести, що на всій області визначення виразу виконується нерівність

,

де кількість радикалів – довільне число.

Доведення. Очевидно, що структура виразу дозволяє суттєво спростити його, використовуючи перетворення лівої частини за допомогою співвідношення

.

Ми виберемо інший підхід, який є простішим. Побачивши, що вираз монотонно зростає на всій своїй області визначення, знаходимо його найменше значення. Воно, як легко бачити, придорівнює. Цим самим нерівність доведена.

При доведенні деяких нерівностей використовуються властивості опуклих функцій. Зокрема, якщо функція на відрізкуопукла вгору, то для двох довільних різних точоквиконується нерівність. Якщо ж функціяна відрізкуопукла вниз, то для двох довільних різних точоквиконується нерівність. Наведемо приклади.

Задача 2.1.6. Порівняти числа:

а) та,

б) та.

Розв’язання. У випадку а) розглянемо функцію, яка є опуклою вниз. Тому, використавши нерівність, дістаємо, що

.

У випадку б) розглядаємо функцію , яка є опуклою вгору. Використавши нерівність, дістаємо.

Задача 2.1.7.Числазадовольняють нерівності

,,.

Довести, що всі вони додатні.

Доведення.Насамперед зауважимо, що числає коренями кубічного рівняння

.

Очевидно, що для від’ємнихліва частина рівняння приймає від’ємні значення. Отже, корені можуть бути тільки додатними, що завершує доведення.

В окремих випадках у залежності від постановки задачі доцільно досліджувати необхідні умови. Наприклад, необхідною умовою того, щоб рівняння мало два корені, сума яких більша 2, а добуток був більший 3, відповідно до теореми Вієта, є виконання системи нерівностей. У даному випадку система несумісна і поставлена задача розв’язків не має. Але, якщо ми цю ж задачу сформулюємо для рівнянняі отримаємо системуіз розв’язками, то одержаної нерівності ще не достатньо, щоб вважати задачу розв’язаною. Обов’язково потрібно врахувати умову існування коренів у вигляді нерівності. Звідси, оскільки, отримуємо.

Зауважимо, що відшукання необхідних умов не є обов’язковим етапом розв’язування задач. Наприклад, при розв’язуванні нерівності нема потреби займатися знаходженням її області визначення, оскільки нерівністьрівносильна заданій.

Розглянемо подібну до попередньої наступну задачу.

Задача2.1.8.При яких значеннях параметрарівняннямає два корені, які обидва більші від 1?

Помилковий розв’язок, запропонований авторами даної задачі в одному із навчальних посібників, виглядає так. Умова задачі рівносильна системі нерівностей

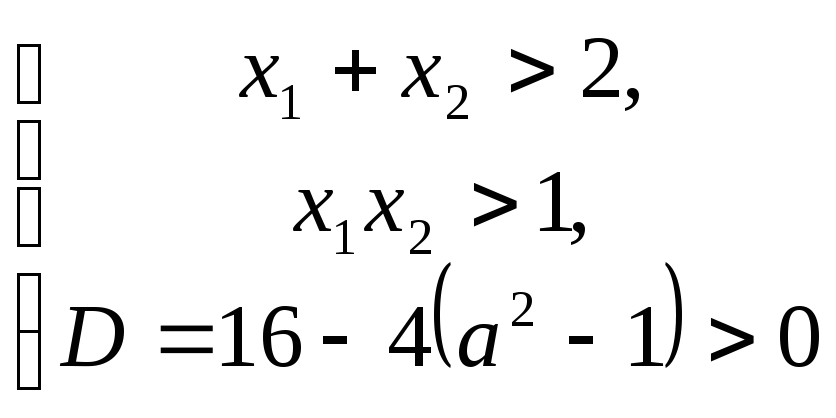(- корені рівняння),

звідки, оскільки перша нерівність системи виконується (сума коренів дорівнює 4), а друга записується у виді , отримуємо розв’язок.

Помилка у наведених міркуваннях полягає у тому, що записана система виражає необхідну, але не достатню умову того, що обидва корені більші від 1. Адже, щоб добуток двох чисел був більший 1, зовсім не обов’язково, щоб кожне з них перевищувало 1. Правильний розв’язок може виглядати наступним чином. Оскільки абсциса вершини параболи дорівнює 2 і розташована правіше точки, то для відшукання розв’язку задачі достатньо вимагати, щоб виконувалися умовита. Розв’язавши систему нерівностей, отримуємо.

Задача 2.1.9. При яких значеннях параметраточкає точкою екстремуму функції ?

Розв’язання. Згідно з умовою задачі, похіднау точціповинна перетворюватись у 0. Це дозволяє отримати значення. Проте, як легко переконатися, функціяу точціекстремуму не має.

Отже, точка при жодному значенні параметране може бути точкою екстремуму заданої функції.

Задача 2.1.10. При яких значеннях параметрасума квадратів коренів рівняннябуде найменшою?

Розв’язання. За теоремою Вієта. Тоді

,

але стверджувати, що значення , при якому одержаний вираз приймає мінімальне значення, є шуканим, ще рано. Потрібно додатково дослідити умову існування дійсних коренів. Знаходимо, звідкита. Як бачимо, числоодержаним інтервалам не належить. Тому, оскільки на знайдених інтервалах функціямонотонна, мінімальне значення виразубуде в одній із точок. Очевидно, що такою точкою є.