
- •Роман Собкович, Наталія Кульчицька Основні методи доведення нерівностей
- •2014 Зміст
- •1.1. Доведення нерівностей за допомогою означення
- •1.2. Синтетичний метод доведення нерівностей
- •1.3. Аналітичний метод доведення нерівностей
- •1.4. Доведення нерівностей методом від супротивного
- •1.5. Метод підсилення при доведенні нерівностей.
- •1.6. Доведення нерівностей методом математичної індукції
- •1.7. Класичні нерівності між середніми та їх доведення
- •1.8. Наслідки з нерівності Коші та задачі на відшукання найбільших та найменших значень
- •2.1. Оцінка областей визначення та множини значень. Монотонність. Опуклість
- •2.2. Застосування властивостей квадратного тричлена
- •2.3. Застосування похідної
- •2.4. Застосування інтеграла.
- •2.5. Опуклі функції та їх застосування до доведення нерівностей. Нерівність Єнсена
- •2.6. Нерівність Юнга
2.3. Застосування похідної
Розглянемо, як при доведені нерівностей можна використовувати похідну. Суть цього прийому полягає в наступному.
Нехай на певному проміжку
![]() із області визначення функцій
із області визначення функцій![]() та
та![]() потрібно довести нерівність
потрібно довести нерівність![]() .
Введемо в розгляд функцію
.
Введемо в розгляд функцію![]() .
Нехай похідна
.
Нехай похідна![]() має на відрізку, що розглядається, єдиний
корінь
має на відрізку, що розглядається, єдиний
корінь![]() ,
це значення є точкою мінімуму функції
,
це значення є точкою мінімуму функції![]() ,
а також виконується нерівність
,
а також виконується нерівність![]() .
Тоді цього достатньо, щоб стверджувати,
що на проміжку
.
Тоді цього достатньо, щоб стверджувати,
що на проміжку![]() виконується нерівність
виконується нерівність![]() .
.
Даний прийом можна використовувати і при доведенні числових нерівностей. Для цього спочатку вводять у розгляд деяку функцію, яка приймає задані числові значення у певних точках, після чого приступають до реалізації описаної вище схеми.
Наведемо приклади таких доведень.
Задача 2.3.1.Довести нерівність
![]() .
.
Доведення. ОДЗ:![]() .
Очевидно, що при
.
Очевидно, що при![]() ми отримуємо рівність. Розглянемо
функцію
ми отримуємо рівність. Розглянемо
функцію![]() .
Її похідна
.
Її похідна![]() дорівнює 0 в точці
дорівнює 0 в точці![]() і монотонно зростає (останнє випливає
з того, що її похідна
і монотонно зростає (останнє випливає
з того, що її похідна![]() додатна). Таким чином, для функції
додатна). Таким чином, для функції![]() точка
точка![]() є точкою екстремуму, а саме точкою
мінімуму. Тому для всіх
є точкою екстремуму, а саме точкою
мінімуму. Тому для всіх![]() ,
що належать ОДЗ, виконується нерівність
,
що належать ОДЗ, виконується нерівність![]() ,
що і потрібно було довести.
,
що і потрібно було довести.
Зауважимо, що одночасно нами фактично
розв’язане рівняння
![]() з єдиним коренем
з єдиним коренем![]() та нерівність
та нерівність![]() з розв’язками
з розв’язками
![]() .
.
Задача 2.3.2.При![]() виконується нерівність
виконується нерівність![]() .
Довести.
.
Довести.
Доведення.Розглянемо функцію![]() .
Знайшовши
.
Знайшовши![]() та
та![]() ,
бачимо, що друга похідна перетворюється
в 0 у точці
,
бачимо, що друга похідна перетворюється
в 0 у точці![]() і при переході через цю точку змінює
знак із «-» на «+». Це означає, що для
функції
і при переході через цю точку змінює
знак із «-» на «+». Це означає, що для
функції![]() точка
точка![]() є точкою мінімуму і
є точкою мінімуму і![]() .
Таким чином,
.
Таким чином,![]() на всій числовій осі. Звідси випливає,
що функція
на всій числовій осі. Звідси випливає,
що функція![]() монотонно зростає. Оскільки
монотонно зростає. Оскільки![]() ,
то при
,
то при![]() маємо
маємо![]() .
Нерівність доведена.
.
Нерівність доведена.
Одночасно нами отримано наступні результати:
рівняння
![]() має єдиний корінь
має єдиний корінь![]() ;
;
нерівність
![]() має розв’язки
має розв’язки![]() .
.
розв’язками нерівності
![]() є проміжок
є проміжок![]() .
.
Задача 2.3.3.Довести, що при![]() для всіх натуральних
для всіх натуральних![]() виконується нерівність
виконується нерівність![]() (нерівність Бернуллі).
(нерівність Бернуллі).
Доведення.При![]() нерівність вірна. Нехай
нерівність вірна. Нехай![]() .
Розглянемо функцію
.
Розглянемо функцію![]() .
Її похідна
.
Її похідна![]() перетворюється в нуль у єдиній точці
перетворюється в нуль у єдиній точці![]() ,
яка, як легко бачити,, є точкою мінімуму.
Тому для всіх
,
яка, як легко бачити,, є точкою мінімуму.
Тому для всіх![]() виконується нерівність
виконується нерівність![]() ,
тобто
,
тобто![]() .
З одержаного співвідношення випливає
нерівність Бернуллі.
.
З одержаного співвідношення випливає
нерівність Бернуллі.
Задача 2.3.4.Довести, що при![]() виконується нерівність
виконується нерівність
![]() .
.
Доведення. Розглянемо тільки випадок![]() ,
оскільки при
,
оскільки при![]() перепозначення змінних
перепозначення змінних![]() на
на![]() та
та![]() на
на![]() приведе нас до аналогічних міркувань.
При
приведе нас до аналогічних міркувань.
При![]() маємо очевидну рівність. Нехай
маємо очевидну рівність. Нехай![]() .
Введемо заміну
.
Введемо заміну![]() та розглянемо функцію
та розглянемо функцію![]() .
Очевидно, що похідна
.
Очевидно, що похідна![]() не перетворюється в нуль у жодній точці
і, оскільки
не перетворюється в нуль у жодній точці
і, оскільки![]() та
та![]() ,
то
,
то![]() ,
монотонно зростаючи, не може приймати
від’ємних значень.
Тому
,
монотонно зростаючи, не може приймати
від’ємних значень.
Тому![]() ,
що доводить задану нерівність.
,
що доводить задану нерівність.
Задача 2.3.5. Довести нерівність![]() (приклад 2.2.10).
(приклад 2.2.10).
Доведення. Нехай![]() .
Розглянемо функцію
.
Розглянемо функцію![]() .
Її похідна
.
Її похідна![]() перетворюється в нуль у точці
перетворюється в нуль у точці![]() .
Очевидно, що це є точка мінімуму і
.
Очевидно, що це є точка мінімуму і![]() .
Оскільки
.
Оскільки![]() ,
то
,
то![]() ,
що фактично і потрібно було довести.
Рівність виконується при
,
що фактично і потрібно було довести.
Рівність виконується при![]() .
.
Задача 2.3.6.Довести, що для всіх
дійсних![]() виконується нерівність
виконується нерівність![]() .
.
Доведення. Розглянемо функцію![]() .
Маємо
.
Маємо![]() .
Рівність похідної нулю досягається при
.
Рівність похідної нулю досягається при![]() .
Очевидно, що знайдене значення є точкою
мінімуму. Для значень
.
Очевидно, що знайдене значення є точкою
мінімуму. Для значень![]() буде виконуватися нерівність
буде виконуватися нерівність![]() .
Рівність виконується при
.
Рівність виконується при![]() .
.
Задача 2.3.7.Довести, що для всіх
дійсних![]() виконується нерівність
виконується нерівність
![]() .
.
Доведення. Розглянемо функцію![]()
![]() .
Похідна
.
Похідна![]() приймає значення 0 в єдиній точці
приймає значення 0 в єдиній точці![]() .
Очевидно, що це значення є точкою
мінімуму. Тому для значень
.
Очевидно, що це значення є точкою
мінімуму. Тому для значень![]() буде виконуватися нерівність
буде виконуватися нерівність![]()
![]() .
Рівність досягається при
.
Рівність досягається при![]() .
.
Задача 2.3.8.Довести, що![]() для всіх натуральних
для всіх натуральних![]() .
.
Доведення. Розглянемо функцію![]() та знайдемо її похідну. Маємо
та знайдемо її похідну. Маємо![]() .
Оскільки
.
Оскільки
![]() ,
,
то на проміжках
![]() ,
,![]() похідна має принаймні по одному кореню.
Більше коренів рівняння
похідна має принаймні по одному кореню.
Більше коренів рівняння![]() мати не може. Справді, рівняння
мати не може. Справді, рівняння![]() має єдиний корінь (оскільки
має єдиний корінь (оскільки![]() і
і![]() для достатньо великих
для достатньо великих![]() ).
Тому функція
).
Тому функція![]() має єдину точку екстремуму – а саме
точку мінімуму, а рівняння
має єдину точку екстремуму – а саме
точку мінімуму, а рівняння![]() у нашому випадку має тільки два корені.
Таким чином обґрунтовано, що похідна
у нашому випадку має тільки два корені.
Таким чином обґрунтовано, що похідна![]() на проміжку
на проміжку![]() приймає додатні значення і функція
приймає додатні значення і функція![]() зростає. Отже,
зростає. Отже,![]() .
Нерівність
.
Нерівність![]() на проміжку
на проміжку![]() виконується для довільних
виконується для довільних![]() ,
тому і для всіх натуральних
,
тому і для всіх натуральних![]() ,
вибраних у цій множині.
,
вибраних у цій множині.
Зауважимо, що інше доведення цієї нерівності методом математичної індукції наведене нами у виді задачі 1.6.3.
Задача 2.3.9.Довести нерівність![]() .
.
Доведення. Зробимо наступні перетворення:
![]() .
.
Перший множник отриманого виразу приймає
тільки додатні значення. Покажемо, що
і другий множник теж завжди додатний.
Для цього розглянемо функцію
![]() .
Її похідна
.
Її похідна![]() перетворюється в нуль в точках
перетворюється в нуль в точках![]() та
та![]() .
Легко переконатися, що при
.
Легко переконатися, що при![]() екстремуму нема, а точка
екстремуму нема, а точка![]() є точкою мінімуму. Оскільки
є точкою мінімуму. Оскільки![]() ,
то функція приймає тільки додатні
значення.
,
то функція приймає тільки додатні
значення.
Задача 2.3.10.Порівняти числа![]() та
та![]() .
.
Розв’язання. Порівняємо натуральні
логарифми цих чисел, тобто числа![]() та
та![]() ,
що рівносильне поставленій задачі,
оскільки функція
,
що рівносильне поставленій задачі,
оскільки функція![]() монотонно зростає на своїй області
визначення. Для цього розглянемо функцію
монотонно зростає на своїй області
визначення. Для цього розглянемо функцію![]() ,
визначену на інтервалі
,
визначену на інтервалі![]() .
Встановимо проміжки її монотонності.
Очевидно, що похідна
.
Встановимо проміжки її монотонності.
Очевидно, що похідна![]() перетворюється в нуль у точці
перетворюється в нуль у точці![]() .
Легко встановити, що це точка максимуму
і що на проміжку
.
Легко встановити, що це точка максимуму
і що на проміжку![]() функція монотонно спадає. Оскільки
цьому проміжку належать числа
функція монотонно спадає. Оскільки
цьому проміжку належать числа![]() та
та![]() ,
то більшому з них відповідає менше
значення функції. Тому
,
то більшому з них відповідає менше
значення функції. Тому![]() і
і![]()
![]() .
.
Задача 2.3.11.
Довести,щопри![]() виконується нерівність
виконується нерівність
![]() .
.
Доведення.
Доведемо нерівність
![]() ,
яка на вказаному проміжку рівносильна
заданій. Розглянемо функцію
,
яка на вказаному проміжку рівносильна
заданій. Розглянемо функцію![]() на інтервалі
на інтервалі![]() та доведемо, що на ньому вона зростає.
Для цього достатньо показати, що
та доведемо, що на ньому вона зростає.
Для цього достатньо показати, що![]() .
Маємо
.
Маємо
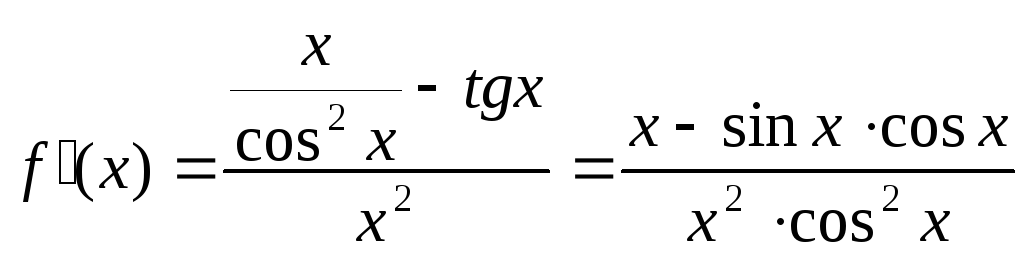 .
.
Оскільки знаменник похідної на вказаному
проміжку додатний, то покажемо, що
додатним є також чисельник, тобто, що
виконується нерівність
![]() .
А це випливає з нерівності
.
А це випливає з нерівності![]() для
для![]() та
та![]() при
при![]() .
Отже,
.
Отже,![]() і функція
і функція![]() зростає на інтервалі
зростає на інтервалі![]() .
Тому
.
Тому![]() для
для![]() або
або![]() .
.
