
- •Многочлени
- •§1. Многочлени від однієї змінної Кільце многочленів
- •§2. Подільність многочленів а) Ділення з остачею
- •Б) Ділення многочлена на лінійний двочлен
- •В) Подільність многочленів
- •Властивості подільності
- •Найбільший спільний дільник
- •Найменше спільне кратне
- •Г) Звідність многочленів
- •Д) Корені многочленів
- •§2.Многочлени над числовими полями а)Многочлени над полем с
- •Б) Многочлени над полем r
- •В) Многочлени над полем q
- •§3.Многочлени від багатьох змінних а) Загальні відомості
- •Б) Симетричні многочлени
Найбільший спільний дільник
4
Спільний
дільник многочленів f(x)
та g(x),
який ділиться на кожний інший спільний
дільник цих многочленів, називається
їх найбільшим
спільним
дільником
(НСД) і позначається (f,g).
НСД многочленів визначається однозначно
з точністю до сталого множника (оскільки,
якщо d(x)
– НСД , то
й c·d(x),
де
![]() ,теж НСД).
,теж НСД).
Многочлени f(x) та g(x) називаються взаємно простими, якщо кожний їхній спільний дільник є ненульовою константою, тобто (f,g)=1.
Розглянемо спосіб знаходження НСД (алгоритм Евкліда).
Нехай
дано многочлени f(x)
та g(x),
причому
![]() .
Виконаємо послідовне ділення з остачею:
.
Виконаємо послідовне ділення з остачею:
![]()
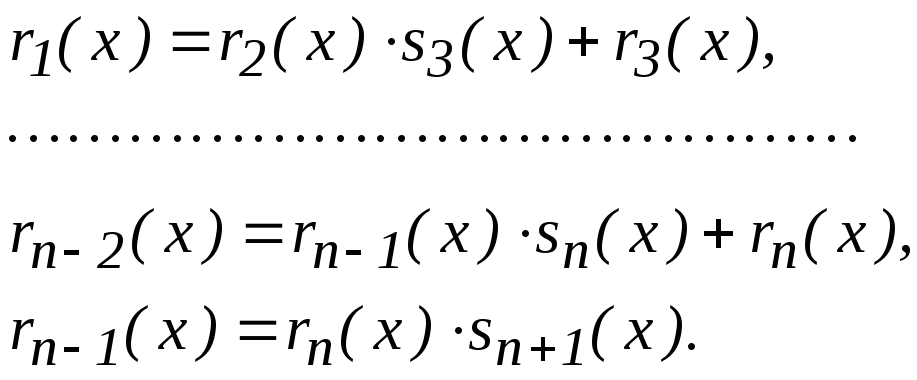
Тут
![]() оскільки послідовність степенів
многочленівg(x),
r1(x),
r2(x),...
є монотонно
спадною. Оскільки степінь r1(x)
не вищий за m-1,
де
m=deg
g,
то кількість кроків в алгоритмі не
перевищує m.
оскільки послідовність степенів
многочленівg(x),
r1(x),
r2(x),...
є монотонно
спадною. Оскільки степінь r1(x)
не вищий за m-1,
де
m=deg
g,
то кількість кроків в алгоритмі не
перевищує m.
Оскільки (f,g)=(g,r1)=(r1,r2)=(r2,r3)=…=(rn-1,rn)=(rn,0)=rn, то остання відмінна від нуля остача rn(x) в алгоритмі Евкліда і є НСД многочленів f(x) і g(x).
Приклад.
З допомогою алгоритму Евкліда знайти НСД многочленів
f(x)=x3–3x2+3x–1, g(x)=x3–1.
x3–3x2+3x–1=(x3–1)·1+(-3x2+3x)
x3–1=(-3x2+3x)·(![]() )+(x–1)
)+(x–1)
-3x2+3x=(x–1)·(-3x).
Отже, (f,g)=x–1.
НСД більшої кількості многочленів, зокрема, f1(x), f2(x),…, fn(x) шукають так:
d1(x)=(f1,f2), d2(x)=(d1,f3), d3(x)=(d2,f4), …, dn-1(x)=(dn-2,fn).
dn-1(x) і є НСД многочленів f1(x), f2(x),…, fn(x).
Якщо хоча б два многочлени із системи f1(x), f2(x),…, fn(x) взаємно прості, то НСД усіх цих многочленів дорівнює одиниці.
Якщо позначити d(x)=rn(x), то, піднімаючись вгору рівностями алгоритму Евкліда, можна отримати вираз
d(x)=f(x)·u(x)+g(x)·v(x),
тобто
![]() такі що(f,g)
виражається через f(x)
і g(x).
такі що(f,g)
виражається через f(x)
і g(x).
Найменше спільне кратне
Найменшим спільним кратним (НСК) многочленів f(x) та g(x) називається спільне кратне f(x) і g(x), на яке ділиться довільне інше спільне кратне цих многочленів. Позначається [f, g].
Теорема. Для довільних ненульових многочленів f(x), g(x) НСК існує і
визначається з точністю до сталого множника.
Доведення.
Для доведення розглянемо многочлен
![]() який,
очевидно, є спільним кратним f(x)
та g(x),
оскільки ділиться на кожний з них. Нехай
s(x)
–довільне інше спільне кратне многочленів
f(x)
і g(x).
Тоді
який,
очевидно, є спільним кратним f(x)
та g(x),
оскільки ділиться на кожний з них. Нехай
s(x)
–довільне інше спільне кратне многочленів
f(x)
і g(x).
Тоді
![]() і
і
![]() ,
звідкиs(x)=s1(x)·f(x),
а також
,
звідкиs(x)=s1(x)·f(x),
а також
![]() тобто
тобто
![]()
Замінимо f(x)=(f,g)·f1(x), g(x)=(f,g)·g1(x), де (f1,g1)=1. Звідси
![]() .
.
Із
(f1,g1)=1
випливає, що
![]() тобто s1(x)=g1(x)·t(x),
звідки
тобто s1(x)=g1(x)·t(x),
звідки
![]() Отже,
Отже,![]()
Це означає, що q(x) – найменше спільне кратне многочленів f(x) та g(x).
Якщо
q1(x)
– інше
НСК, то
![]() і
і![]() ,
тобтоql(x)
та
q(x)
відрізняються тільки сталим множником.▲
,
тобтоql(x)
та
q(x)
відрізняються тільки сталим множником.▲
Г) Звідність многочленів
Многочлен
f(х)![]() Р[x]
називається незвідним
у полі Р,
якщо він не є константою і не
має
дільників, відмінних від константи та
асоційованих з ним многочленів (аналог
простого числа). В іншому випадку
многочлен називають звідним
(аналог
складеного числа). Поняття звідності є
відносним і залежить від поля Р, над
яким розглядається многочлен.
Р[x]
називається незвідним
у полі Р,
якщо він не є константою і не
має
дільників, відмінних від константи та
асоційованих з ним многочленів (аналог
простого числа). В іншому випадку
многочлен називають звідним
(аналог
складеного числа). Поняття звідності є
відносним і залежить від поля Р, над
яким розглядається многочлен.
Приклад.
Многочлен
f(х)=x![]() незвідний
у полі Q, але звідний у полі R:
незвідний
у полі Q, але звідний у полі R:
f(x)=
(x-![]() )(x+
)(x+![]() );
);
многочлен
f(x)= x![]() +3
незвідний в полях Q, R, але звідний у полі
С:
+3
незвідний в полях Q, R, але звідний у полі
С:
f(x)=
(x-i![]() )(x+i
)(x+i![]() ).
).![]()
Якщо многочлен f(х) незвідний у полі Р, то він вже є добутком незвідних в даному полі многочленів (один співмножник). Якщо многочлен f(х) звідний у полі Р, то, розклавши його і всі його співмножники в добуток незвідних многочленів у даному полі, отримаємо зображення многочлена, яке називають розкладом многочлена f(х) на незвідні множники:
f(x)=р![]() (х)р
(х)р![]() (х)...р
(х)...р![]() (х),
де р
(х),
де р![]() (х)
– незвідні в полі Р, і=1,2,...,l.
(х)
– незвідні в полі Р, і=1,2,...,l.
Звідси випливає ще один запис многочлена f(x):
f(x)=[p![]() (x)]
(x)]![]() [p
[p![]() (x)]
(x)]![]() …[p
…[p![]() (x)]
(x)]![]() ,
,
де
р![]() (х)
– попарно різні (неасоційовані)
многочлени, незвідні в полі Р.
(х)
– попарно різні (неасоційовані)
многочлени, незвідні в полі Р.
Таке зображення називають канонічним розкладом многочлена f(x) в полі Р.
