2.3. Замкнутая гдс и ее уравнение

Впервые понятие замкнутой ГДС и ее уравнение изложены в [41].

Так как вся системная деятельность, соответствуя понятию замкнутости, должна быть реализована за счет внутренних ресурсов системы, то и процесс реализации взаимодействия элементов системы должен подчиняться этому требованию.

В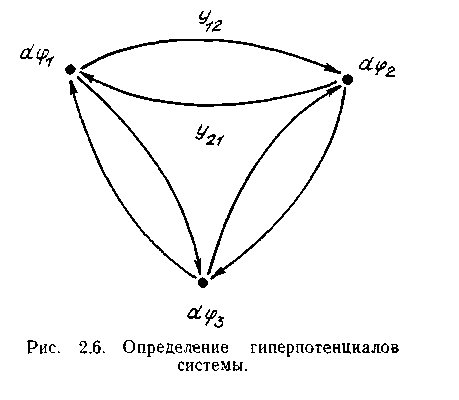заимодействие элементов обусловливается свойствами самих элементов. Способность элементов взаимодействовать отражена в теории ГДС введением понятия гиперкомплексного потенциала элемента системы. Обозначим эту величину φ_n. Полная системная совокупность потенциалов отдельных элементов φ образует гиперпотенциал всей системы.

Реализация взаимодействия — это превращение потенциальной возможности взаимодействуя конкретных элементов в их взаимосвязь.

Естественно, что степень связи между разными элементами может быть разной. Из этого следует, что и способность к образованию связей должна иметь относительный характер, определяемый как направлением взаимодействия, так и разновидностью взаимодействующих элементов.

В процессе взаимодействия каждый элемент системы, как это следует из условия замкнутости, расходует себя на образование всех своих взаимодействий с другими элементами. Даже процесс наблюдения за ходом реализации взаимосвязей — это тоже частный случай взаимодействия (элемент — наблюдатель), требующий расхода ресурса взаимодействий для наблюдаемого элемента. Сам факт наблюдения (учитывая важность измерительных операций в процессе становления научных концепций) основан на овеществлении потенциальных возможностей элементов к взаимодействию. Более того, то, что мы называем элементом ( в процессе измерения, восприятия), по сути своей есть не весь элемент, а только реализуемая во взаимодействии его часть.

Изложенные особенности, рассматриваемые в обратном порядке, позволяют представить элемент dφ_n как гиперкомплексную совокупность всех взаимодействий, реализуемых данным элементом со всеми элементами системы.

Проиллюстрируем сказанное конкретным примером одноуровневой ГДС третьего порядка (рис. 2.6), имеющей полный набор связей для каждого элемента.

Необходимо отметить, что произвольный элементА_п системы S и его гиперпотенциал φ_n (в более точном измерительном смысле dφ_n ) связаны функциональным отношением в виде

Двойная направленность стрелок у знака равенства в выражении (2.10) свидетельствует об условности выбора точки отсчета при раскрытии содержательного аспекта таких понятий, как элемент и гиперпотенциал; зачастую эти понятия отождествляются по содержанию в границах системной методологии.

Согласно изложенному с учетом одноуровневой ГДС третьего порядка (рис.2.6) запишем для первого элемента

гдеdφ_n — изменение (расход) первого элемента в процессе взаимодействий; y₁₂ — эквивалент удельной интенсивности взаимодействия первого элемента со вторым; y₁₃ — взаимодействие первого и третьего элементов; — знак взаимодействия.

Аналогично рассуждая, получаем для второго и третьего элементов

Для упрощения записи заменяем знак гиперкомплексного взаимодействия знаком обычного сложения, не забывая о его ГДС-характере.

Перенося все слагаемые в (2.11) — (2.13) в левую сторо­ну, группируя по индексам, получаем систему уравнений, описывающую ГДС согласно рис. 2.6

Перепишем(2.14), используя матричную форму записи

Обобщая полученные результаты и вводя сокращенную форму записи, определяем из (2.15}

где Y — полная матрица взаимодействий; φ — матрица гипер-потенциалов.

Выражение (2.16) представляет собой уравнение замкнутой ГДС. Правая часть, равная нулю, символизирует отсутствие внешних воздействий у рассматриваемой системы (случай идеальной, полной замкнутости).

Отметим ряд особенностей, вытекающих из анализа уравнения (2.16).

1. Известно, что частное решение матричного уравнения можно записать в виде [31]

где Δ_п — алгебраическое дополнение элемента у_пп матрицы Y; Δ — определитель матрицы Y.

Так как правая часть (2.16) всегда равна нулю, то в (2.17) получаем неопределенность, раскрывая которую (например, по правилу Лопиталя [31]), можно найти решение.

2. Из (2.16) и (2.17) для случая нетривиального решения следует необходимость

Выражение (2.18) назовем условием существования замкнутой ГДС.

Объединяя в одно целое (2.16) и(2.17), получаем полную систему уравнений замкнутой ГДС для случая дискретного (матричного) описания ее свойств

3. Понятие замкнутости — идеализированное понятие, которое никогда не может быть реализовано на практике во всей полноте. Поэтому в (2.18) с практических позиций точнее было бы говорить не о равенстве, а о стремлении к нулю. Эта особенность приводит к возникновению проблемы наблюдаем ости исследуемых объектов: чем больше нарушается требование (2.18), тем менее наблюдаем исследуемый объект.

4. В общем случае гиперпотенциал, как и другие системные понятия, может иметь сложную ГДС-структуру и отражаться с помощью гиперкомплексной матрицы, рассмотренной в предыдущих параграфах.

4. Важнейшая особенность матрицы взаимодействий Y — расположение единиц на ее главной диагонали. По своему содержанию эти единицы являются гиперкомплексными величинами, которые на практике могут быть овеществлены (воплощены в конкретную теоретическую или практическую форму) в любом виде. Все единицы матрицы Y отличаются друг от друга своим качественным содержанием в силу свойства гиперкомплексности. Это отличие выражается ее позиционным индексом, который совпадает с номером соответствующей клетки матрицы Y.

Гиперкомплексные единицы (в общем случае) не подчиняются обычным правилам сложения, а требуют соблюдения условий, реализующих гиперкомплексное взаимодействие.