31.6. Непрерывные случайные величины

Если множество значений случайной величины Xзаполняет (непрерывно) конечный или бесконечный промежуток на число­вой оси, то такая случайная величина называетсянепрерывной.

Можно дать другое, более строгое, определение, используя понятие функции распределения.

Случайная величина Xназываетсянепрерывной, если ее функция распределенияF(x) непрерывна на всей числовой оси.

Для непрерывной случайной величины Xпри любом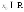имеет место равенство

а также

где F(x) – функция распределения величиныX.

Помимо функции распределения для непрерывных случай­ных величин существует еще один удобный способ задания зако­на распределения – плотность распределения вероятностей.

Пусть функция распределения F(x) данной непрерывной случайной величиныXнепрерывна и дифференцируема всюду, кроме, может быть, отдельных точек.

Плотностью распределения вероятностей непрерывной случайной величиныназывают первую производную от функ­ции распределения:

Часто вместо термина плотность распределенияисполь­зуют терминыплотность вероятностей, илидифференци­альная функция, или простоплотность.

Основные свойства плотности вероятностей

Пусть f(x) – плотность вероятностей.

1.

2.

График плотности распределения вероятностей f(x) называ­етсякривой распределения.

3.Вероятность того, что непрерывная случайная величинаХпримет значение, принадлежащее интервалу (a;b), определяется равенством

4.Функция распределенияF(x) выражается через плотность вероятностейf(x) формулой

Математическое ожидание непрерывной случайной ве­личины Хс плотностью распределения вероятностейf(x) находят по формуле

(31.16)

При этом математическое ожидание существует, если интеграл в правой части формулы (31.16) абсолютно сходится (это значит, что сходится интеграл

В частности, если все возможные значения принадлежат интервалу (a;b), то

Все свойства математического ожидания, указанные выше для дискретных случайных величин, сохраняются и для непре­рывных величин.

Дисперсия непрерывной случайной величины Х, возмож­ные значения которой принадлежат всей осиOx, определяется равенством

или равносильным равенством

В частности, если все возможные значения Хпринадлежат интервалу (a;b), то

или

Все свойства дисперсии, указанные для дискретных случай­ных величин, сохраняются и для непрерывных величин.

Среднее квадратичное отклонение непрерывной случай­ной величиныопределяется аналогичным образом, как и для дискретной величины:

На практике применяются и другие числовые характерис­тики непрерывных случайных величин.

МодойМ₀(Х) непрерывной случайной величиныХназыва­ется такое ее значение, при котором плотность вероятностей имеет максимум.

Медианой М_е(Х) непрерывной случайной величины Х называ­ется то ее возможное значение, которое определяется равенством

Геометрически медиану можно истолковать как точку, в ко­торой ордината f(x) делит пополам площадь, ограниченную кривой распределения.

Пример 1. Случайная величина X задана функцией распределения

Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (–1; 1).

Решение. Вероятность того, что X примет значение, заключенное в интервале (a; b), равна приращению функции распределения на этом интервале:

Положив a = –1, b = 1, получим

Пример 2. Пусть плотность вероятностей f(x) случайной величины X задана с помощью равенств

Найти коэффициент a.

Решение. Коэффициент a определяем с помощью равенства

отсюда

Пример 3. Плотность вероятностей случайной величины Х задана формулой

Найти ее числовые характеристики: математическое ожидание, дисперсию, среднеквадратическое отклонение.

Решение. Найдем математическое ожидание, используя формулу (31.16):

Вычислим дисперсию:

Отсюда найдем среднеквадратическое отклонение: