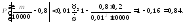31.10. Закон больших чисел

Под законом больших чиселв теории вероятностей понимается ряд теорем, в каждой из которых устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным.

Неравенство Маркова.Если случайная величинаХпринимает неотрицательные значения и имеет математическое ожиданиеM(X), то для любого > 0 имеет место неравенство:

Это неравенство, очевидно, равносильно следующему

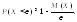
Неравенство Чебышева.Пусть имеется случайная величинаХс математическим ожиданиемM(X) и дисперсиейD(X). Каково бы ни было положительное число, вероятность того, что величинаХотклоняется от своего математического ожидания не меньше чем на, ограничена сверху числом

(31.19)

Неравенство Чебышева (31.19) можно записать в эквивалентной форме, если перейти от события 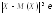к противоположному событиюТогда получим:

Если случайная величина Химеет биномиальное распределение с математическим ожиданиемM(X) = npи дисперсиейD(X) = npq, то неравенство Чебышева имеет вид

Для относительной частоты событияAвnнезависимых испытаниях, в каждом из которых оно может произойти с вероятностьюp, неравенство Чебышева примет вид

(31.20)

Неравенство Чебышева позволяет доказать ряд важных теорем, объеденных общим названием «закон больших чисел». Основная из этих теорем принадлежит самому П. Л. Чебышеву.

Теорема Чебышева.ПустьX₁,X₂, …,X_n, … – последовательность независимых случайных величин, имеющих дисперсии, которые ограничены одной и той же постояннойC. Тогда, каково бы ни было постоянное положительное число,

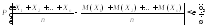
Из последнего неравенства следует предельное равенство

Теорема Чебышева показывает, что среднее арифметическое большого числа случайных величин как угодно мало отличается (с вероятностью близкой к 1) от среднего арифметического их математических ожиданий.

Если то теорема Чебышева примет вид

Теорема Бернулли. Пусть производится n независимых опытов, в каждом из которых с вероятностью p может наступить некоторое событие A. Если число наступлений этого события при n независимых испытаниях равно m, то для любого  > 0 выполняется

Теорема Бернулли утверждает устойчивость относительной частоты при постоянных условиях опыта. Устойчивость относительной частоты при переменных условиях опыта устанавливает теорема Пуассона.

Если в последовательности независимых испытаний p_i – вероятность появления события A в i – m испытании, а m – число появлений события при n испытаниях, то для любого  > 0 выполняется

Пример 1. Среднее число дождливых дней в году в данном районе равно 60. Оценить вероятность того, что в этом районе будет менее 200 дождливых дней в году.

Решение. Пусть Х – число дождливых дней в году. По неравенству Маркова

откуда получаем

Пример 2. Средний срок службы механизма равен 3 годам. Оценить снизу вероятность того, что данный механизм не прослужит более 18 лет.

Решение. Пусть случайная величина Х – срок службы механизма. Из условия задачи следует, что M(X) = 3. Требуется оценить снизу вероятность P(X) < 18, которую можно рассматривать как левую часть неравенства Маркова при условии, что  = 18. Тогда

Пример 3. Всхожесть семян некоторого растения составляет 80 %. Найти вероятность того, что при посеве 10 000 семян отклонение доли взошедших семян от вероятности того, что взойдет каждое из них, не превзойдет по модулю 0,01.

Решение.

Из условия следует, что n = 10 000,  = 0,01, p = 0,8, q = 0,2. В соответствии с формулой (31.20) получаем