31.8. Функция одного случайного аргумента

Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то эта случайная величина называется функцией случайного аргу­мента (случайной величины) Х. В этом случае пишут:

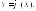
Если Х – дискретная случайная величина и функция монотонна, то возможные значенияY находят из равенства

где x_i– возможные значения случайной величиныХ.

Вероятности возможных значений случайной величины Yнаходят из равенства

Если – немонотонная функция, то различным зна­чениям случайной величиныХмогут соответствовать одинако­вые значения случайной величиныY. В этом случае вероятность повторяющегося значения случайной величиныYравна сумме вероятностей тех возможных значенийХ, при которых случай­ная величинаYпринимает одно и то же значение.

Математическое ожидание и дисперсия случайной величи­ны Yопределяются соответственно равенствами

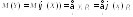
и

,

где

Если Х– непрерывная случайная величина с плотностью распределенияf(x) и если– дифференцируемая строго возрастающая или строго убывающая функция, то плотность распределенияg(y) случайной величины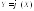выражается формулой

где – функция, обратная функции

Если же функциянемонотонная в промежутке воз­можных значенийХ, то весь указанный промежуток разбивается на n промежутков монотонности и обратная функция 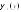нахо­дится на каждом из них. Плотность распределенияслучай­ной величиныопределяется в этом случае по формуле

Для нахождения математического ожидания и дисперсии слу­чайной величины можно воспользоваться формулами

Пример 1. Пусть закон распределения случайной величины Х имеет вид:

Х	–2	–1	0	1	2	3
P	0,1	0,2	0,4	0,02	0,15	0,13

Найти закон распределения величины

Решение. Возможные значения случайной величины Y это (–2)², (–1)², 0², 1², 2², 3², т. е. 0, 1, 4, 9. Их вероятности:

Таким образом, закон распределения случайной величины Y будет:

Y	0	1	4	9
P	0,4	0,22	0,25	0,13

Пример 2. Случайная величина Х равномерно распределена в интервале (–1; 1). Найти плотность вероятностей случайной величины Y = 3X.

Решение. Найдем плотность распределения f(x) случайной величи­ны Х. Величина Х равномерно распределена в интервале (–1; 1), поэто­му в этом интервале имеем

вне рассматриваемого интервала – f(x) = 0.

Так как функция y = 3x дифференцируема и строго возрастает, то применима формула

где – функция, обратная функцииy = 3x.

Найдем

Найдем

Найдем производную

Очевидно, что

Таким образом, Так какy = 3x, причем 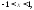тоСледовательно, в интервале (–3; 3) искомая плотность распределения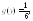вне этого интервала

Контроль:

31.9. Функция двух случайных аргументов

Рассмотрим систему двух случайных величин (X,Y). Если каждой паре (x,y) возможных значений случайных величинХиYсоответствует одно возможное значение, вычисляемое по определенному закону, случайной величиныZ, тоZназываютфункцией двух случайных аргументов X и Y:

Для практики важное значение имеет задача определения закона распределения суммы двух случайных величин: Z = X + Y.

Пусть ХиY– дискретные независимые случайные величины. Чтобы найти распределение функцииZ = X + Y, надо найти все возможные значенияZ. Для этого достаточно сложить каждое возможное значениеХсо всеми возможными значениямиY. Вероятности найденных значенийZравны произведениям вероятностей складываемых значенийХиY.

Если ХиY– непрерывные независимые случайные величины, то плотность распределенияg(z) суммыZ = X + Y(при условии, что плотность распределения хотя бы одного из аргументов задана в интервалеодной формулой) может быть найдена по формуле

или по равносильной формуле

где f₁,f₂– плотности распределения аргументов.

Если возможные значения аргументов неотрицательны, то плотность распределения g(z) величиныZ = X + Yнаходят по формуле

(31.17)

или по равносильной формуле

(31.18)

Формулы (31.17) и (31.18) называют формулами свертки, илиформулами композиции двух распределений, а функциюg(z) –сверткой функцийf₁(х) иf₂(х); закон распределения сум­мыZ = X + Yдвух независимых случайных величин называюткомпозицией (сверткой)законов распределения слагаемых.

Если обе плотности f₁(х) иf₂(у) заданы на конечных интервалах, то для отыскания плотностиg(z) величиныZ = X + Yцелесообразно сначала найти функцию распределенияG(z), а затем – плотность распределенияg(z):

Если ХиY– независимые случайные величины, заданные соответственно плотностями распределенияf₁(х) иf₂(х), то вероятность попадания случайной точки (X;Y) в областьDнаходят по формуле

Пример 1. Дискретные независимые случайные величины X и Y заданы распределениями:

Х	1	3		Y	2	4
P	0,2	0,8		P	0,4	0,6

Найти распределение случайной величины Z = X + Y.

Решение. Возможные значения Z есть суммы каждого возможного значения X со всеми возможными значениями Y:

Найдем вероятности этих возможных значений. Для того чтобы Z = 3, достаточно, чтобы величина X приняла значение x₁ = 1 и величина Y – значение y₁ = 2. Вероятности этих возможных значений, как следует из данных законов распределения, соответственно равны 0,2 и 0,4. Так как аргументы Х и Y независимы, то события X = 1 и Y = 2 независимы и, следовательно, вероятность их совместного наступления по теореме умножения равна

Аналогично найдем:

Напишем искомое распределение, предварительно сложив вероятности несовместных событий

Z	3	5	7
P	0,08	0,44	0,48

Осуществим контроль:

Пример 2. Найти закон распределения суммы Z = X + Y, если величины X и Y независимы и каждая из них распределена равномерно на отрезке [0; 1].

Решение. Имеем

и

Величина Z = X + Y принимает в этом случае значения из промежутка [0; 2], вне этого промежутка ее плотность вероятностей равна нулю.

При имеем:

Так как при t < 0 равен нулю первый множитель f₁(t) подынтегрального выражения, а при t > z равен нулю второй множитель заменим интервал по всей оси интервалом по отрезку [0;z].

При имеем:

При равен нулю второй множительибо тогдаприt > 1 равен нулю первый множитель f₁(t).

Таким образом,

Пример 3. Заданы плотности распределения независимых равномерно распределенных случайных величин X и Y:

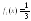в интервале (0; 3), вне этого интервала

в интервале (0; 3), вне этого интервала

Найти функцию распределения и плотность распределения случайной величины Z = X + Y. Построить график плотности распределения g(z).

Решение. По условию, возможные значения X определяются неравен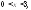ством возможные значенияY – неравенством Отсюда следует, что возможные случайные точки (X; Y) расположены в квадрате OABC (рис. 31.7).

Рис. 31.7

По определению функция распределения равна

Неравенству x + y < z удовлетворяют те точки (z; y) плоскости xOy, которые лежат ниже прямой x + y = z (эта прямая отсекает на осях Ox и Oy отрезки, равные z). Если же брать только возможные значения x и y, то неравенство x + y < z выполняется только для точек, лежащих в квадрате OABC ниже прямой x + y = z.

С другой стороны, так как величины Х и Y независимы, то

где S – величина той части площади квадрата OABC, которая лежит ниже прямой x + y = z.

Очевидно, величина площади S зависит от значения z.

Если тот. е.

Если 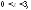то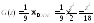(рис. 31.7).

Если то(рис. 31.8).

Рис. 31.8

Площадь фигуры OAHKC найдена как разность между площадью квадрата OABC (которая равна 3² = 9) и площадью прямоугольного треугольника HBK, т. е.

Если z > 6, то

Таким образом, искомая функция распределения такова:

Найдем плотность распределения:

График плотности распределения g(z) изображен на рис. 31.9.

Рис. 31.9