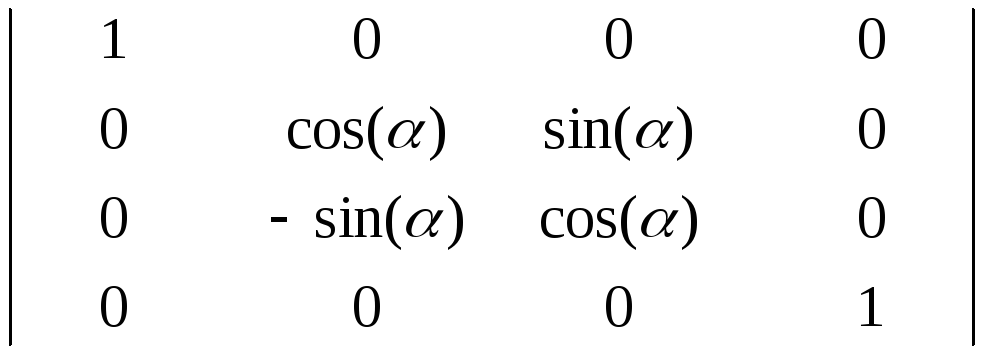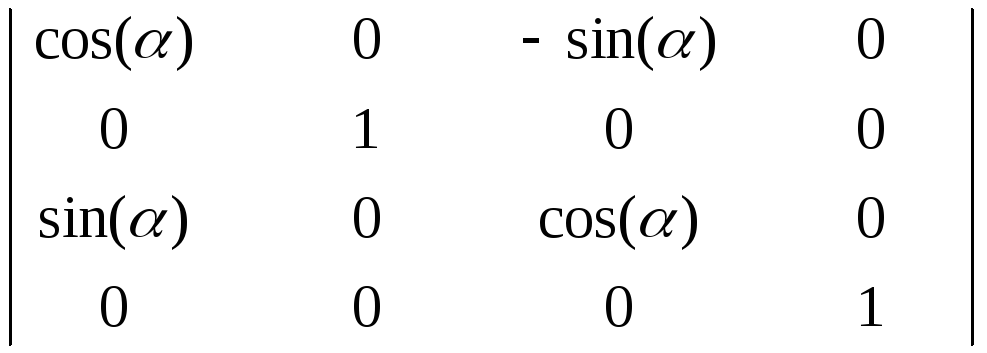Варіанти завдання

Таблиця 2.1

Параметри завдання для практичного виконання

№ п/п	Фігура	Параметри траєкторії руху крапки
1.	Трикутник	x = 1:0.1:6
2.	Прямокутник	x = 1:0.2:6
3.	Квадрат	x = 1:0.1:5
4.	Паралелограм	x = 1:0.1:6
5.	Ромб	x = 1:0.1:7
6.	Трикутник	x = 1:0.2:8
7.	Прямокутник	x = 1:0.1:6
8.	Квадрат	x = 1:0.1:5
9.	Паралелограм	x = 1:0.2:6
10.	Ромб	x = 1:0.1:7
11.	Трикутник	x = 1:0.1:8
12.	Прямокутник	x = 1:0.2:6
13.	Квадрат	x = 1:0.1:5
14.	Паралелограм	x = 1:0.1:6
15.	Ромб	x = 1:0.1:7
16.	Трикутник	x = 1:0.2:8
17.	Прямокутник	x = 1:0.1:6
18..	Квадрат	x = 1:0.1:5
19.	Паралелограм	x = 1:0.2:6
20.	Ромб	x = 1:0.1:7

Контрольні запитання

1. Що таке анімація?

2. Які існують методи побудови анімації?

3. Назвіть основні типи анімації?

4. Поясніть технологію побудови анімацію методом «покадрових рухів».

5. Поясніть технологію побудови анімацію методом «ключових кадрів».

6. Що таке морфінг?

7. Що собою представляє розрахункова анімація?

8. Яка різниця між імітацією і анімацією?

9. Яким чином може бути побудована анімація в середовищі MATLAB?

10. Якими способами може задавить перетворення при побудові анімації?

Практична робота №3 Перетворення у тривимірному просторі

Мета роботи: практичне вивчення математичних основ комп’ютерної графіки та ознайомлення з можливостями графопобудови у тривимірному просторі в MATLAB.

Інформаційна частина

Перетворення у тривимірному просторі.

Абсолютно всі операції, які можна виконувати у двомірному просторі, можуть бути застосовані і для тривимірного простору. Це обумовлюється тим, що будь-яка фігура двомірного простору, з додаванням третьої координати, може бути представлено у тривимірному просторі. Це ніби зсув двомірної фігури по перетинаючій її площині із з’єднанням їх крайніх полігонів. В будь-якому випадку, для фігур у тривимірному просторі застосовуються ті ж самі методи та операції перетворення, і при роботі в однорідних координатах матриці перетворень/операцій будуть складатися не з трьох, а з чотирьох стовпців.

Зсув фігури. Операція зсуву реалізовується з використанням матриці перетворення (зсуву) з попереднім представленням фігури у системі однорідних тривимірних координат:

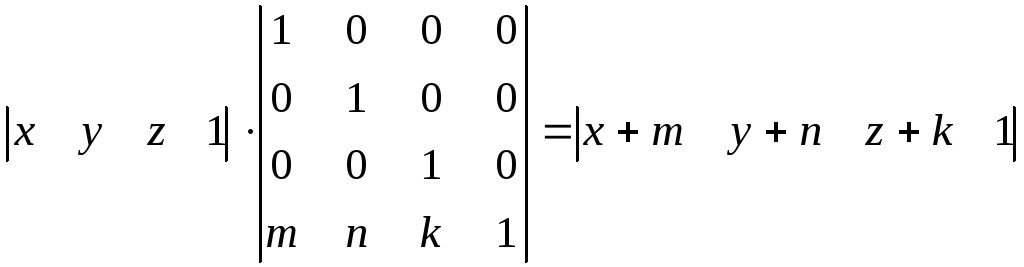
Масштабування фігури. Операція масштабування реалізовується з використанням матриці перетворення (зміни масштабу) з попереднім представленням фігури у системі однорідних тривимірних координат:

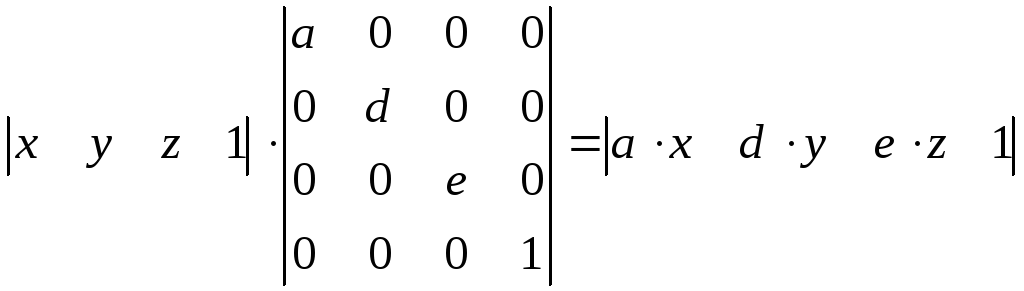
Загальне повне масштабування фігури. Операція загального повного масштабування відрізняється від попередньої тим, що масштабування виконується з використанням коефіцієнта масштабу, який задається в рядку і стовпці однорідних координат:

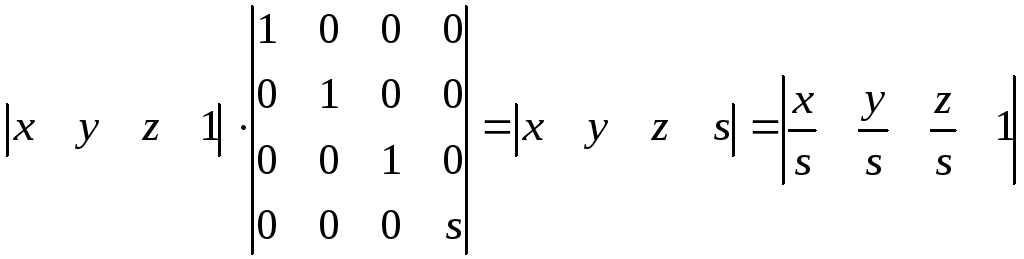
Поворот фігури навколо точки (m, n, k) на кут α.

Аналогічно, як і для двомірного перетворення, необхідно розкласти дану операцію на базові (найпростіші) операції, а саме: 1) перенесення тіла на вектор A(-m,-n,-k) для суміщення точки (m, n, k) з початком координат, 2) поворот тіла на кут α; 3) перенесення тіла на вектор A'(m, n, k) для повернення його у вихідне положення. Якщо уявити, що фігура представлена набором точок (вершин фігури), можна записати наступні операції: 1) - 3) з кожної з них; в матричної формі це представляється наступним чином (R(α) – матриця повороту навколо осі x, y або z):

Матриці повороту навколо осей x, y, z на кут α, матимуть наступний вигляд:

Rx =
Ry =
Rz =