Инжинерная графика,начертательная геометрия, лекции / Конспект Лекций НачерГеом 2093 (ДонИЖТ)

5. МЕТОДЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА

План

5.1Цель преобразования чертежа

5.2Метод замены плоскостей проекций

5.3Метод плоско-параллельного перемещения.

5.4.Вращение вокруг линии уровня

5.5 Вращение вокруг оси перпендикулярной плоскости проекций

5.1 Цель преобразования чертежа

Решение многих задач в начертательной геометрии значительно упрощается, если геометрические объекты занимают частное положение, т.е. проецируются в натуральную (или в минимальную) величину.

Цель преобразований чертежа – достичь того, чтобы прямая или плоскость общего положения стала параллельной (или перпендикулярной) плоскости проекций, т.е. проецировалась в натуральную (или в минимальную) величину.

Кметодам преобразования комплексного чертежа относят следующие:

-метод замены плоскостей проекций;

-метод плоско-параллельного перемещения;

-методы вращения вокруг линии уровня и вокруг оси перпендикулярной плоскости проекций.

5.2 Метод замены плоскостей проекций

Этот метод заключается в том, что положение геометрических объектов в пространстве остается неизменным, а систему плоскостей проекций дополняют новой плоскостью

проекций, параллельной или перпендикулярной заданной прямой или плоскости и обязательно перпендикулярной π1 или π2. На новую плоскость проекций заданная прямая

или плоскость будет проецироваться в натуральную или минимальную величину, а после разворота новой плоскости проекций в общую плоскость чертежа эту величину можно измерить.

На рис. 5.2.1 показано, как введена новая плоскость проекций π4 (π4 π1), которая по оси х14 пересекает π1. Расстояние от точки А до А1 (координата ZА) сохраняется и у А4 – проекции т. А на π4, следовательно А4А14=А2А12=АА1= ZА; после совмещения плоскости π4 с π1 по оси х14 проекция А1 и новая проекция А4 лежат на одной линии связи, перпендикулярной к новой оси проекции х14.

Рисунок 5.2.1

31

Способом замены плоскостей проекций найдем натуральную величину отрезка прямой общего положения (рис 5.2.2).

Для определения натуральной величины отрезка АВ вводим новую плоскость проекций π4 так, чтобы π4 была перпендикулярна π1. При этом π4 должна быть параллельной АВ, т.е. А1В1 должна быть параллельной оси х14 – линии пересечения π4 и π1. Развернув π4 в плоскость чертежа, получим проекцию А4В4, равную н.в. АВ. Чтобы построить проекцию прямой АВ на π4 необходимо из А1 и В1 провести перпендикулярно х14 линии связи в плоскость π4 и отложить в π 4 от оси х14 расстояния, равные координатам Z точек А

иВ. На концах отложенных отрезков получим А4

иВ4. Проекция А4В4 является искомой проекцией прямой АВ в натуральную величину.

Рисунок 5.2.2

Определим расстояние между двумя параллельными прямыми (рисунок 5.2.3).

Для решения этой задачи необходимо выполнить замену плоскостей проекций дважды, поскольку прямые занимают общее положение относительно

плоскостей проекций. Сначала вводим π4 (π4 π1 и

π4║а║в, т.е х14║а1║в1) и определяем натуральную

величину прямых а и в, как а4 и в4. Далее вводим π5

(π4 π5, а также π5 а	и π5 в, т.е. х45 а4 и х45 в4) и
получаем проекции а5	и в5 в минимальную величину –
каждая прямая проецируется на π5 в точку, т.к. она

перпендикулярна π5. Чтобы построить проекции прямой а5 и в5 на π5 необходимо из а4 и в4 провести перпендикулярно х45 линии связи в плоскость π5 и отложить в π5 от оси х45 расстояния, равные расстояниям от а1 и в1 до х14. На концах отложенных отрезков получим а5 и в5. Откладываемые равные расстояния на рисунке отмечены одинаковыми

засечками.	Искомым	расстоянием	между
параллельными прямыми		а и в в данном случае
является расстояние между проекциями а5 и в5.

Рисунок 5.2.3

32

Определим натуральную величину двугранного угла при ребре АВ (рисунок 5.2.4).

Известно, что двугранный угол спроецируется в натуральную величину, если его проекция будет в виде плоского угла, при этом ребро, при котором он образован, должно быть спроецировано в точку. Решение задачи начнем с анализа положения ребра АВ относительно плоскостей проекций. Ребро АВ является отрезком фронтальной прямой, т.е. на π2 АВ спроецировано в натуральную величину (АВ = А2В2). Следовательно, для решения задачи достаточно выполнить один раз замену плоскостей проекций, чтобы получить проекцию АВ в минимальную величину. Вводим плоскость π4, при условии π4 π2 и

π4 АВ, т.е х24 А2В2. Откладываем в π4 от х24 расстояния, равные координатам Y точек А, В, С, D.

Они где измеряются от А1, В1, С1, D1 по линиям

связей до Х12 и отмечены засечками в π1 и π4. В π4 получаем плоский угол с вершиной А4 ≡ В4, который

определяет натуральную величину двугранного угла.

Рисунок 5.2.4

Построим н.в. треугольника АВС методом замены плоскостей проекций (рисунок 5.2.5). Для решения этой задачи необходимо преобразовать систему плоскостей проекций таким образом, чтобы треугольник АВС оказался параллельным одной из плоскостей проекций. В нашем случае все стороны занимают общее положение, следовательно, ни одна из сторон не спроецирована в натуральную величину. Поэтому, необходимо построить в треугольнике АВС прямую частного положения – горизонталь h (можно

фронталь).		Вводим	плоскость π4		(π4 π1	и
π4 h,	т.е	х14 h1)	и	получаем	проекцию
прямой	h	в точку А	4,	а плоскости АВС		в

прямую А4В4С4. Вторая замена: вводим плоскость π5 перпендикулярно π4 и параллельно АВС, т.е х45║ А4В4С4. На плоскость π5 треугольник АВС проецируется без искажения (А5В5С5), в н.в.

Рисунок 5.2.5

5.3 Метод плоско-параллельного перемещения.

Этот метод заключается в том, что заданную прямую или плоскость общего

положения перемещают таким образом, чтобы привести её в частное положение, параллельное или перпендикулярное какой-либо плоскости проекций. Для этого одну из проекций заданной прямой или плоскости перемещают в плоскости чертежа до положения параллельного иди перпендикулярного оси (х).

33

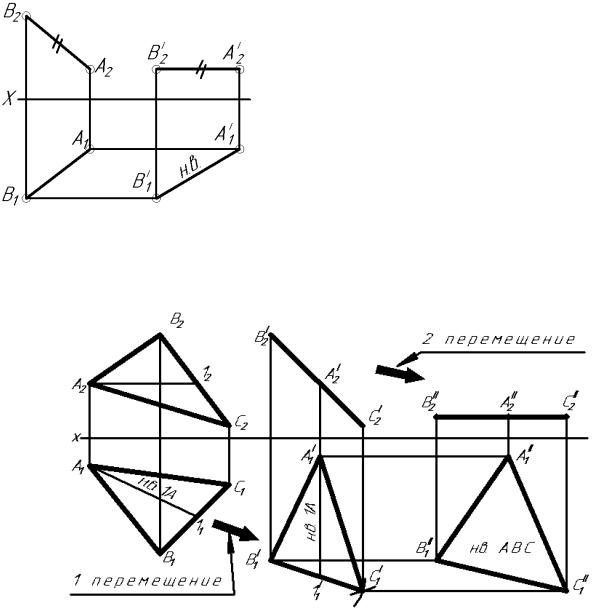
	Определим натуральную величину отрезка АВ
	способом плоско-параллельного перемещения (рисунок
	5.3.1). Переместим в π2	фронтальную проекцию А2В2 в
	новое положение АI2ВI2	, параллельное оси х. при этом
	прямая АВ займет частное положение, параллельное π1,
	т.е спроецируется на π1 в н.в (проекция АI1ВI1). Проекции
	АI1 и ВI1 найдем на пересечении горизонтальных линий
	связи из А1 и В1 с вертикальными линиями связи из АI1 и
	ВI1, соответственно. Аналогичным образом можно было
	бы переместить в π1 горизонтальную проекцию А1В1 в
Рисунок 5.3.1	положение, параллельное оси х, а на π2 получить
	проекцию АВ в н.в.

Определим натуральную величину треугольника АВС способом плоско-параллельного перемещения (рисунок 5.3.2).

Рисунок 5.3.2

В нашем случае все стороны занимают общее положение, следовательно, нужно построить горизонталь или фронталь и относительно этой прямой осуществлять перемещение треугольника АВС. Построим горизонталь 1А в проекциях А212 и А111. Первое перемещение проекции А1В1С1 производим в π1 таким образом, чтобы треугольник АВС занял проецирующее положение по отношению к π2, т.е чтобы 1А спроецировалась на π2 в точку а весь треугольник – в прямую (т.е. в перемещенной проекции A|1B|1C|1 горизонталь А|11|1 оси х). Второе

перемещение – осуществим в π2: расположим АI2ВI2СI2 параллельно оси х плоскости π1 в новое

положение A||2B||2C||2. При этом АВС будет параллелен π1 и полученная проекция A||1B||1C||1 является натуральной величиной треугольника АВС.

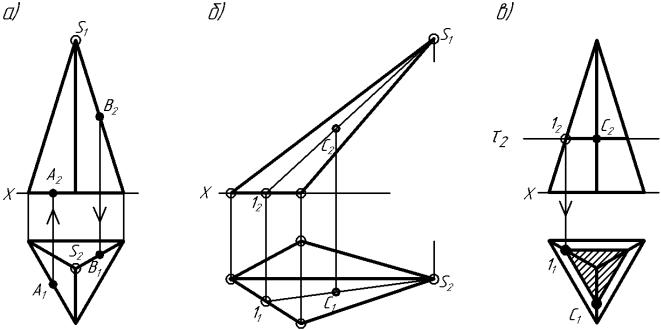
5.4. Вращение вокруг линии уровня

Линиями уровня называют горизонталь и фронталь. Чтобы придать заданной геометрической фигуре (плоскости) частное положение (на этом принципе основано решение задач любым способом преобразования чертежа), ее вращают вокруг горизонтали или фронтали до тех пор, пока данная фигура не расположится параллельно плоскости проекции, спроецировавшись в н.в. (рисунок 5.4.1).

34

Рисунок 5.4.1

В качестве примера рассмотрим плоскость, заданную пересекающимися перпендикулярными прямыми АО h, которая вращением вокруг горизонтали h приведена в положение

параллельное π1. Если радиус вращения ОА займет положение, параллельное плоскости π1, то новая горизонтальная проекция проекция О1А|1 будет равна н. в. ОА. Значит на комплексном чертеже (правая часть рисунка 5.4.1) достаточно любым способом найти н.в. ОА (напр. методом треугольника), отложить её как О1А|1 перпендикулярно h1 (по теореме о проецировании прямого угла), и плоскость АО h будет параллельна π1. Для нахождения новых проекций

любой точки, лежащей в плоскости АО h, можно использовать вспомогательную прямую, на которой лежали бы: искомая точка и точки пересечения вспомогательной прямой с АО и h.

Рис. 5.4.1 иллюстрирует общий принцип построения при решении задач методом вращения вокруг линии уровня.

		Определим угол между двумя пересекающимися
		прямыми m	и n (рисунок 5.4.2).
		Для решения задачи строим фронталь 12, вокруг
		которой будем вращать прямые m и n до положения,
		при котором угол между m и n, т.е. вся плоскость m n
		спроецируется в н.в. на π2. Согласно теореме о
		проецировании прямого угла из проекции точки
		пересечения	прямых А2	строим перпендикуляр к
		проекции прямой 1222 и на их пересечении получим
		О2. При вращении плоскости m n вокруг 12 проекция
		точки А2 будет описывать дугу, радиус которой r =
		ОА, после вращения, должен спроецироваться в н.в.
		Определим значение радиуса вращения r (н.в. ОА)
		методом прямоугольного треугольника. Для этого
		перпендикулярно О2А2 из А2			строим отрезок А2А*
		равный разнице YА – YО, измеренной на π1 (отмечен
		засечкой). Соединив О2 с концом отложенного отрезка
		А*, получим	r = н.в.ОА	– радиуса вращения.		В π2
	Рисунок 5.4.2	перпендикулярно 1222 из О2			строим отрезок	О2А/2
		длиной r. (вокруг прямой 1222			осуществили вращение

до положения параллельного π2) и получ кем н. в. угла между m и n, а также плоскости, которую эти прямые определяют.

35

5.5 Вращение вокруг оси перпендикулярной плоскости проекций

1-у проекцию фигуры вращают вокруг оси перпендикулярной плоскости проекций, чтобы 2- ая спроецировалась в н.в.

	Найдем н.в. АВ (рисунок 5.5). Развернем
	вращением вокруг				прямой	а	(а	π2, т. В а)
	отрезок АВ до положения параллельного π1. Для
	этого	в	π2	проекцию		А2В2		разворачиваем
	относительно			В2	в новое положение АI2В2,
	параллельное оси х. При этом						АВ займет частное
	положение, параллельное π1, т.е спроецируется на π1
	в н.в (проекция АI1В1). Положение АI1 найдем на
	пересечении горизонтальной лини связи из А1 с
	вертикальной линией связи из АI2							. Аналогичным
	образом можно было бы развернуть в π1
	горизонтальную проекцию А1В1						в положение, ║-ое
Рисунок 5.5	оси х,	а	на	π2	получить проекцию АВ в н.в.

Выводы:

Метод замены плоскостей проекций реализуется путем введения новой плоскости проекций относительно неподвижной прямой или плоскости общего положения, которая спроецируется на новую плоскость проекций в натуральную или в минимальную величину в зависимости от того параллельна или перпендикулярна данная прямая или плоскость новой плоскости проекций.

Метод плоско-параллельного перемещения заключается в перемещении и повороте одной из проекций прямой или плоскости общего положения до положения параллельного (или перпендикулярного) оси х, чтобы другая проекция этой прямой или плоскости стала проецироваться в натуральную (или минимальную) величину.

Метод вращения вокруг линии уровня предусматривает неподвижность плоскостей проекций, а заданная плоскость должна оборачиваться вокруг своей линии уровня до положения параллельного плоскости проекций, которое соответствует проекции радиуса вращения в натуральную величину на данную плоскость проекций.

Все методы обязательно требуют для плоскостей введения линий уровня: фронтали или горизонтали.

Определить натуральную величину плоскости общего положения можно, применив метод замены плоскостей проекций или метод плоско-параллельного перемещения дважды; для определения н.в. отрезка достаточно одного раза.

Вопросы для самопроверки

1.Для чего нужны методы преобразования комплексного чертежа?

2.Какие способы преобразования чертежа рассмотрены в разделе?

3.В чем заключается различие между способами преобразования чертежа?

4.Какое положение в системе плоскостей проекций занимает дополнительная плоскость?

5.Какое количество плоскостей нужно ввести, чтобы определить натуральную величину треугольника, занимающего общее положение?

6.В чем заключается метод плоско-параллельного перемещения?

7.В чем заключается метод вращения вокруг линии уровня?

8.Какие задачи можно решать, используя рассмотренные методы?

Задачи для самостоятельной работы.

1.Определить н.в. плоскости АВС, - А (80;25;35), В (55;10;60), С(40;45;45) методами: а) замены плоскостей проекций; б) плоско-параллельного перемещения;

в) вращения вокруг линии уровня.

2. Найдите н.в. двугранного угла, образуемого плоскостями АВС и АВD: А (65;25;25),

В (40;7;50), С (15;50;40), D (25;5;20).

36

6. МНОГОГРАННИКИ

План

6.1Основные понятия. Точки на поверхности многогранников.

6.2Пересечение многогранников прямыми.

6.3Сечения многогранников плоскостями.

6.4Пересечение многогранников.

6.5Построение разверток поверхностей многогранников.

6.1 Основные понятия. Точки на поверхности многогранников.

Многогранником называется геометрическое тело, поверхность которого со всех сторон образована пересекающимися плоскими многоугольниками

Главные элементы поверхности многогранника:

-грани – плоскости, образующие поверхность многогранника;

-ребра – линии пересечения сопредельных граней;

-вершины – точки пересечения ребер.

Многогранники бывают выпуклые и вогнутые. Выпуклым называется многогранник, вся поверхность которого расположенная по одну сторону от любой его грани. Правильным многогранником называют такой выпуклый многогранник, у которого все грани – одинаковые правильные многоугольники, и все многогранные углы при вершинах равны (тетраэдр,

гексаэдр - куб, октаэдр, додекаэдр, икосаэдр).

Построение комплексных чертежей многогранников сводится к построению проекций их геометрических элементов: граней, ребер, вершин, то есть проекций плоских фигур, отрезков прямых и точек, правила изображение которых были изучены ранее.

Наиболее распространены в инженерной практике: призмы и пирамиды.

Призма – многогранник, две грани которого одинаковые многоугольники, лежащие в параллельных плоскостях (основания призмы), а другие грани – параллелограммы (боковые грани). Наиболее распространенные виды призм:

1.прямоугольный параллелепипед (включая куб) - боковые грани являются одинаковыми прямоугольниками, перпендикулярными прямоугольным основаниям;

2.прямая призма - боковые грани и ребра перпендикулярны основаниям (рисунок 6.1.1, а);

3.наклонная призма – боковые грани образуют с основаниями непрямые углы (рис. 6.1.1,б, в).

Рисунок 6.1.1

Пусть т. В (рисунок 6.1.1 а ), лежащая на передней боковой грани призмы, задана одной проекцией В2. Т.к. названная грань является горизонтально-проецирующей плоскостью, то на π1 она проецируется в прямую, на которой по линии связи определяем В1. Пусть т. А, лежащая на

37

верхнем основании призмы, задана одной проекцией А1. Т.к. названная грань является

фронтально-проецирующей плоскостью, то на π2 она	проецируется в прямую, на
которой по линии связи определяем А2.
Пусть т. С (рисунок 6.1.1 б ) задана одной проекцией С2	и лежит на наиболее удаленной
от π2 боковой грани наклонной призмы. Т.к. названная грань является плоскостью общего

положения, то для нахождения С1 проводим в этой грани через известную проекцию т.С вспомогательную прямую 12, на горизонтальной проекции которой находим С1. Т.е. сначала проводим во фронтальной проекции грани 1222 через С2, после по линиям связи находим точки 11 и 21, далее на 1121 по линии связи находим С1.

Пусть т. С (рисунок 6.1.1 в ) задана одной проекцией С2 и лежит на наиболее удаленной от π2 боковой грани наклонной призмы. Т.к. названная грань является плоскостью общего положения, то для нахождения С1 заключаем т. С во вспомогательную секущую плоскость горизонтального уровня, которую зададим фронтальным следом τ2. Плоскость τ пересечет ребра призмы в точках 1, 2, 3, фронтальные проекции которых 12, 22, 32 – точки пересечения τ2 с фронтальными проекциями ребер призмы. По линиям связи на соответствующих горизонтальных проекциях ребер найдем 11, 21, 31. Треугольник 123 является контуром сечения призмы плоскостью τ, образующие контур сечения прямые 12, 23, 13 – лежат в боковых гранях призмы, т. С лежит на контуре сечения (прямой 12) в заданной грани. На проекции 1121, лежащей на наиболее удаленной от π2 горизонтальной проекции боковой грани находим по линии связи С1.

Т.о., проекции точек на поверхности многогранника находят с помощью:

-линий связи, если грань, на которой расположена искомая точка, является проецирующей плоскостью (рисунок 6.1.1 а );

-вспомогательных прямых (рисунок 6.1.1 б ) или вспомогательных секущих плоскостей (рисунок 6.1.1 в ), если грань, на которой расположена искомая точка, является плоскостью общего положения.

Пирамида – многогранник, одна грань которого произвольный многоугольник (основание пирамиды), а другие грани – треугольники (боковые грани), которые имеют общую вершину. Пирамиды бывают прямые (рисунок 6.1.2 а, в) и наклонные (рисунок 6.1.2 б ). У прямой пирамиды вершина, в которой пересекаются боковые грани, проецируется в центр тяжести основания, лежащего в плоскости проекций.

Рисунок 6.1.2

38

На рисунке 6.1.2 а показано нахождение неизвестной проекции точки по одной известной проекции и заданному местоположению точки. Для точки А задана проекция А1 и местоположение на ребре основания пирамиды. Т.к. основание пирамиды на π2 проецируется в прямую, то на этой прямой по линии связи находят А2. Для т. В задана В 2 и местоположение на боковом ребре, на горизонтальной проекции которого по линии связи находят В1.

Пусть т. С (рисунок 6.1.2 б ) задана одной проекцией, например, С2 и лежит на наиболее удаленной от π2 боковой грани наклонной пирамиды. Для нахождения С1 проводим в этой грани через известную проекцию т. С вспомогательную прямую 1S, на горизонтальной проекции которой находим С1. Т.е. сначала проводим во фронтальной проекции грани 12S2 через С2, после по линиям связи находим точки 11 и S1, далее на 11S1 по линии связи находим

С1.

Пусть т. С (рисунок 6.1.2 в ) задана одной проекцией С2 и лежит на ребре (может лежать на боковой поверхности) пирамиды. Для нахождения С1 заключаем т. С во вспомогательную секущую плоскость горизонтального уровня, которую зададим фронтальным следом τ2. Плоскость τ пересечет ребро пирамиды в точке 1, фронтальная проекция которой 12 – точка пересечения τ2 с фронтальной проекцией данного ребра пирамиды. По линии связи на соответствующей горизонтальной проекции ребра найдем 11, из которой параллельно линиям основания пирамиды на π1 построим контур сечения пирамиды плоскостью τ. Искомая проекция С1 лежит на контуре сечения в заданной грани поверхности пирамиды. Находим С1 на пересечении линии связи из С2 с контуром сечения в заданной грани.

6.2 Пересечение многогранников прямыми.

Задача сводится к построению точек пересечения прямой в с плоскостями – гранями пирамиды (рисунок 6.2 а – исходный).

Порядок построений:

1. Заключаем прямую в (рисунок 6.2 б ) во фронтально-проецирующую плоскость σ (след σ2), которая пересекает ребра пирамиды в точках 1, 2, 3 (проекции 12, 22, 32).

2. По линиям проекционной связи на горизонтальных проекциях ребер пирамиды находим горизонтальные проекции 11, 21, 31 и соединяем их в горизонтальную проекцию контура сечения пирамиды плоскостью σ.

3. Т.к. прямая в и контур сечения лежат в одной плоскости σ, то они пересекаются: А1, В1

– проекции точек пересечения. Т.к. контур сечения лежит на поверхности пирамиды, то А1, В1 – проекции искомых точек пересечения прямой в с поверхностью пирамиды.

4. По линиям связи на в2	находим А2 и В2.
Определяем видимость в	относительно
пирамиды в проекциях.

Рисунок 6.2

39

6.3 Сечения многогранников плоскостями.

Важнейшей практической задачей является нахождение натуральной величины сечения многогранника плоскостью. На комплексном чертеже пирамиды (рисунок 6.3.1), основанием которой является правильный шестиугольник, пирамиду пересекает фронтально-проецирующая

плоскость σ (задана следом σ2).

Рисунок 6.3.1

Сначала находим фронтальные проекции точек 1…6, в которых σ (σ2) пересекает ребра пирамиды. Далее по линиям связей находим горизонтальные и профильные проекции точек 1…6 на горизонтальных и профильных проекциях ребер пирамиды. Следующий шаг – соединение одноименных проекций точек 1…6 на всех трех плоскостях проекций и получение соответствующих проекций линии контура сечения пирамиды плоскостью σ. Для нахождения н.в. сечения использованы изученные ранее метод замены плоскостей проекций (π4 совпадает с σ, т.е. х24 совпадает с σ2) и метод плоско-параллельного переноса (фронтальная проекция сечения плоско-параллельным перемещением расположена параллельно оси х).

40