Инжинерная графика,начертательная геометрия, лекции / Конспект Лекций НачерГеом 2093 (ДонИЖТ)

8. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ

План

8.1Линия пересечения поверхностей, общий порядок её построения.

8.2Способ вспомогательных секущих плоскостей.

8.3Способ вспомогательных секущих концентрических сфер.

8.1 Линия пересечения поверхностей, общий принцип её построения.

Линией пересечения поверхностей называется линия, состоящая из всех общих точек пересекающихся поверхностей. Чтобы построить линию пересечения строят ряд точек, принадлежащих обеим поверхностям, и соединяют их плавной кривой. Для построения общих точек двух пересекающихся поверхностей используют вспомогательные секущие плоскости или сферы.

Общий порядок построений.

1.Задаётся вспомогательная секущая плоскость или сфера, которая пересекает обе заданные поверхности по линиям (контурам сечений), имеющим в проекциях графически простую форму прямых и окружностей. Секущие плоскости или сферы проводят таким образом, чтобы контуры сечений пересекающихся поверхностей были параллельны или перпендикулярны плоскости проекций.

2.Отмечаются точки пересечения полученных контуров сечений, лежащих в одной секущей плоскости и принадлежащих обеим заданным поверхностям, т.е. искомой линии их пересечения.

3.Повторяются достаточное количество раз операции, изложенные в пунктах 1 и 2, после чего все отмеченные точки пересечения полученных контуров сечений последовательно соединяются в линию пересечения заданных поверхностей.

8.2 Способ вспомогательных секущих плоскостей

Построим линию пересечения конуса со сквозным трехгранным отверстием (рисунок 8.2.1 а). Вспомогательные секущие плоскости проведем параллельно основанию конуса (рисунок 8.2.1 б). Секущие плоскости проводятся так, чтобы каждая из них пересекала обе поверхности. В этом случае контурами сечений конуса будут окружности, проецирующиеся на π1 в н.в., а контурами сечений трехгранного выреза будут прямые, также проецирующиеся на π1 в н.в.

Первая плоскость α проведена через верхнее ребро трехгранного отверстия. Данное ребро и окружность радиусом R – это контуры сечений отверстия и конуса плоскостью α, лежащие в этой плоскости и проецирующиеся на π1 в н.в. В α в проекции на π1 эти ребро и окружность (контуры сечений) пересекаются в проекциях 11 и 21. По линиям связи найдем на α2 проекции 12 и 22. 1 и 2 – точки линии пересечения заданных поверхностей.

Аналогичным образом с помощью еще двух секущих плоскостей находим другие точки и последовательно соединяем их плавными кривыми в одну линию пересечения.

Рисунок 8.2.1

51

							Построим	линию пересечения кривых
						поверхностей: конуса и сферы (рисунок 8.2.2).
						Зададим на фронтальной проекции параллельно
						основанию конуса 5-7 вспомогательных секущих
						плоскостей (на рисунке даны только γ2 и β2) между
						А2	и В2, - проекциями граничных точек пересечения
						контуров обеих поверхностей. Каждая секущая
						плоскость пересекает конус и сферу по
						окружностям с радиусами, определяемыми на
						фронтальной проекции как расстояния от оси
						поверхности до её контурной образующей по
						линии следа секущей плоскости.
							Так секущая плоскость γ пересекает конус по
						окружности, радиус которой – расстояние от точки
						пересечения γ2		с осью конуса до точки пересечения
						γ2 с контурной образующей конуса; для сферы – это
						расстояние от точки пересечения γ2 с вертикальной
						осью сферы до точки пересечения γ2 с контурной
						криволинейной образующей сферы. Оба контура
						сечения – окружности, проецирующиеся на π1 в
						н.в.; центры их горизонтальных проекций
						совпадают с центрами горизонтальных проекций
						конуса и сферы соответственно. Окружности лежат
						в одной плоскости γ, т.е. они пересекутся в C1 и D1,
						по	которым	на γ2 найдем C2 и D2. Остальные
						необходимые точки линии пересечения находим с
	Рисунок 8.2.2					помощью других секущих плоскостей.
Рассмотрим			построение			линии
пересечения			тора	с	цилиндром
(рисунок		8.2.3).		В		качестве
вспомогательных						секущих
плоскостей				использованы
фронтальные плоскости.					Построение
показано для плоскости α (задана α1).
Плоскость пересекает тор по двум
окружностям, радиусы которых АО и
ОВ, а цилиндр – по образующим 1 и
2.	На		чертеже		построены
фронтальные			проекции			этих
окружностей и образующих. Точки
пересечения			К2, L2,		M2	и N2
являются фронтальными проекциями
этих точек, принадлежащих линии
пересечения.			Их	горизонтальные
проекции совпадают с окружностью,

в которую проецируется цилиндр на плоскость π1.

Рисунок 8.2.3

52

8.3 Способ вспомогательных секущих концентрических сфер

Слово «концентрических» означает, что все секущие сферы имеют один центр.

Этот способ применяется при построении линии пересечения поверхностей вращения, оси которых пересекаются. Вспомогательная секущая сфера пересекает поверхность вращения по окружности в случае, когда ее центр лежит на оси этой поверхности вращения.

На рисунке 8.3.1 оси поверхностей вращения (конуса и цилиндра) параллельны π2, и поэтому линии пересечения их с секущими сферами (окружности) проецируется на π2 в виде прямых. На π 1 (на рисунке не показано) эти линии пересечения проецировались бы в н.в. - в виде окружностей. Центры секущих сфер лежат на осях заданных поверхностей вращения.

Рисунок 8.3.1

В качестве примера рассмотрим построение линии пересечения прямого кругового конуса с наклонным цилиндром (рисунок 8.3.2). Оси конуса и цилиндра параллельны фронтальной плоскости проекций и пересекаются в проекции О2, которая принимается за центр вспомогательных секущих сфер. А2 и В2 – проекции точек пересечения контуров пересекающихся поверхностей, определяются без дополнительных построений.

Радиус секущей сферы нужно

выбирать в пределах от Rmin до Rmax . Rmax – радиус наибольшей сферы –

расстояние от центра до наиболее удаленной точки пересечения контурных образующих заданных поверхностей (точка А2). Rmin – радиус наименьшей сферы, вписанной в одну поверхность вращения (коническую) и пересекающей другую (цилиндр).

Рисунок 8.3.2

Наименьшая сфера вписана в коническую поверхность и определяет точку С линии пересечения конуса и цилиндра..

Коническую поверхность данная сфера пересекает по окружности, параллельной горизонту и проецирующейся в виде горизонтального отрезка 1222, а цилиндрическую поверхность эта сфера пересекает также по окружности, проецирующейся в виде 3242. Места пересечений этих отрезков (проекций окружностей) определяют проекции точек (т. С и конкурирующая с ней), принадлежащих линии пересечения заданных кривых поверхностей.

Последующие точки линии пересечения (например: D, N и конкурирующие с ними) получают аналогично, с помощью других вспомогательных секущих сфер (обычно 5-7 сфер).

53

Характерной особенностью рассмотренного примера является то, что проекция линии пересечения построена на одной плоскости проекций.

Если в обе пересекающиеся кривые поверхности может быть вписана сфера с центром в точке пересечения осей этих поверхностей, то последние пересекаются по двум плоским кривым. (Следствие из теоремы Монжа)

На рисунке 8.3.3 в пересекающиеся конус и цилиндр вписана сфера с центром в точке пересечения их осей О2. Линии пересечения конуса и цилиндра плоские кривые – эллипсы, проецирующиеся в отрезки прямых А2В2 и С2D2.

Рисунок 8.3.3

В ряде случаев может быть применен метод эксцентрических секущих сфер, отличающийся тем, что секущие сферы проводят из разных центров, лежащих на оси одной из пересекающихся поверхностей (но всегда так, чтобы сечения имели графически простую форму и точки пересечения сечений легко определялись, образуя линию пересечения заданных поверхностей).

Вопросы для самопроверки.

1.Какие способы применяют для построения линии пересечения кривых поверхностей, кривых и многогранных поверхностей?

2.Каков общий порядок построения линии пересечения поверхностей с помощью вспомогательных секущих сфер или плоскостей?

3.На чем базируется способ вспомогательных секущих сфер?

4.Как определяются минимальный и максимальный радиус секущей сферы

Задачи для самостоятельной работы.

3.Построить линию пересечения двух цилиндров с одинаковыми радиусами, оси которых параллельны π1 и пересекаются под углом 300.

4.Построить линию пересечения двух цилиндров с радиусами 60 мм и 45 мм, оси которых параллельны π2 и пересекаются под углом 450.

5.Построить линию пересечения двух цилиндров с радиусами 50 мм и 35 мм, оси которых параллельны π3 и пересекаются под углом 900.

54

9. РАЗВЕРТКИ КРИВЫХ ПОВЕРХНОСТЕЙ

План

9.1Цилиндрические поверхности.

9.2Конические поверхности.

Развертка кривой поверхности – это плоская фигура, образованная последовательным совмещением всех точек кривой поверхности с одной плоскостью.

9.1Цилиндрические поверхности

Вкачестве примера рассмотрим построение развертки боковой поверхности прямого кругового цилиндра, который пересечен фронтально-проецирующей плоскостью Σ (рисунок 9.1.1). Фигура, полученная в сечении – эллипс. Фронтальная проекция сечения (эллипса)

совпадает с проекцией (следом) секущей плоскости Σ2, а горизонтальная – с окружностью, в которую проецируется цилиндр на π1.

Строим развертку способом нормального сечения (необходимо иметь н.в. нормального сечения (периметр) и н.в. образующей цилиндра). Основание цилиндра, перпендикулярно его

боковой поверхности, т. е. является нормальным сечением, а проекции образующих на π2 даны в н.в.

Рисунок 9.1.1

Основание цилиндра делим в π1 на 12 равных частей, обозначив точки деления: 11, 21…121. Точки деления являются проекциями образующих цилиндра, проецирующихся на π2 в н.в. параллельно оси цилиндра. Фактически, необходимо цилиндрическую поверхность мысленно разрезать по образующей (точка 1) и развернуть её в плоскость чертежа. Чтобы сделать развертку окружности основания цилиндра с точками 1…12 в горизонтальный отрезок, следует определить длину этого отрезка по формуле: L=2πRОСН, где RОСН – радиус основания цилиндра; затем горизонтальный отрезок длиной L разбивают на 12 равных частей, начав и закончив с точки 10. Далее перпендикулярно построенному горизонтальному отрезку из точек 10…120 строим образующие цилиндра, на каждой из которых откладываем расстояния, измеренные от нижнего основания цилиндра до Σ2 по соответствующим образующим (измеряем

55

эти расстояния на π2). Концы отложенных на развертке расстояний соединяем плавной кривой с помощью лекала, в результате чего получаем линию сечения на развертке.

Для более полного представления о построении линии сечения и развертки цилиндра рассмотрим сечение наклонного (косого) цилиндра (рисунок 9.1.2).

Рисунок 9.1.2

Верхнее и нижнее основания цилиндра проецируются на π2 в отрезки прямых вместе со всеми точками на них лежащими, а на π1 в н.в., однако боковая поверхность цилиндра не занимает проецирующего положения. Все предварительные построения (деление основания цилиндра на 12 частей…, построение на чертеже из 12 точек образующих параллельных π2) проводим как в предыдущем случае. Построение развертки выполним способом нормального сечения, для чего зададим секущую плоскость Σ (Σ2) перпендикулярно образующим поверхности цилиндра. Контур сечения – окружность радиусом R, измеряемым на π2 по линии проекции сечения от оси до контурной образующей. Развернем окружность сечения в горизонтальный отрезок длиной 2πR. Разобьем горизонтальный отрезок на 12 равных частей, соответствующих образующим из точек 1…12 и построим эти образующие на развертке перпендикулярно горизонтальному отрезку. На образующих развертки вверх и вниз от горизонтального отрезка откладываем расстояния, измеренные на π2 по соответствующим образующим от Σ2 до верхнего (до точек 1…12) и нижнего оснований цилиндра. Верхние (точки 10…120) и нижние концы отложенных на образующих развертки расстояний соединяем плавными кривыми с помощью лекала.

56

9.2 Конические поверхности.

Рассмотрим построение развертки боковой поверхности конуса (рисунок 9.2.1).

	Рисунок 9.2.1
В результате пересечения конуса плоскостью (след		2) в сечении получается эллипс. Во
фронтальной плоскости проекция эллипса совпадает с		проекцией	секущей	плоскости 2.
Обозначим проекции точек	пересечения секущей	плоскости	(Δ2)	с некоторыми

образующими, а именно: точки		А2, В 2, расположенные на контурных образующих, и
С2 ≡ D2, расположенные	на образующих, занимающих положение профильных прямых.
Построим развертку	боковой	поверхности конуса. Фактически, разрежем конус по

контурной образующей (соответствует т. 1 основания конуса) и развернем в плоскость. Для этого радиусом, равным длине контурной образующей конуса (обозначим L), построим

круговой сектор, длина		дуги которого всегда равна			длине		окружности основания				конуса
2πRОСН. Для нахождения угла α при вершине сектора развертки составим пропорцию:
	Угол сектора α		=	угол всей окружности 3600			α	= 3600	α =	RОСН	3600
	длина дуги сектора 2πR			длина всей окружности 2πL		2πR		2πL		L
	ОСН						ОСН

Далее дугу сектора разбивают образующими на 12 равных частей (точки 10…120), после чего эти же образующие строят на чертеже конуса в двух проекциях (их используют как вспомогательные прямые) и определяют точки их пересечения с контуром сечения , т.е. с 2.: А, В, С, D… Проекцию в н. в. каждой из этих образующих (вместе с точками А, В, С, D…) получим, проецируя их на контурную образующую (соответствует 12 или 72), которая дана в н.в., как фронтальная прямая (при этом проекция D2 займет положение D2* ). Далее отметим на развертке точки А0, В0, С0, D0… на соответствующих комплексному чертежу и развертке образующих. Все эти точки соединим плавной кривой с помощью лекала.

Рассмотрим построение развертки боковой поверхности наклонного конуса (рисунок 9.2.2). Развертка строится с помощью 12-и вспомогательных образующих прямых, которыми

57

равномерно охвачена поверхность конуса путем разбиения окружности основания на 12 равных частей (точки 1…12). Определение н.в. каждой образующей выполнено на π2 благодаря вращению её горизонтальной проекции в π1 до параллельности оси х. На н.в. образующих перенесены проекции точек, полученных в результате сечения образующих конуса с 2

(А0,В0…).

Рисунок 9.2.2

Дальнейшее построение (рисунок 9.2.3) аналогично предыдущему построению развертки прямого конуса.

58

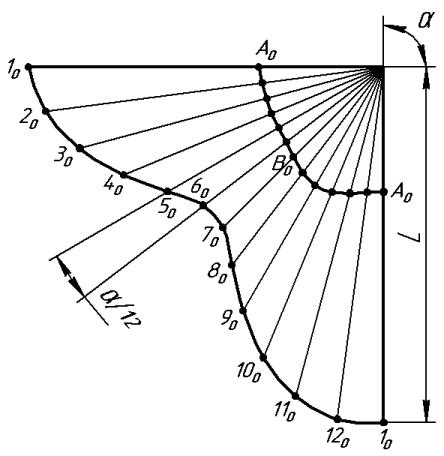
Рисунок 9.2.3

Вопросы для самопроверки.

1.Каков порядок построения разверток цилиндрических поверхностей?

2.Каков порядок построения разверток конических поверхностей?

3.Сформулируйте, в чем заключается способ нормального сечения и для каких поверхностей он применим?

4.Как определяется угол сегмента для развертки конической поверхности?

Задачи для самостоятельной работы.

1.Построить развертку прямого цилиндра с радиусом основания 20 мм и длиной образующей 45 мм, ось которого параллельна π1 , пересекает ось Z и наклонена к π2 под углом 300.

2.Построить развертку прямого конуса с радиусом основания 20 мм и длиной образующей 45 мм, ось которого параллельна π2 , пересекает ось Y и наклонена к π1 под углом 300.

59

Рекомендуемая литература.
1. Інженерна та комп’ютерна графіка: Підручник / В.Є Михайленко, В.М. Найдиш,	А.М.

Підкоритов, І.А. Скидан; За ред. В.Є. Михайленка. – 2-ге вид., перероб. – Вища шк., 2001. – 350с.: іл.

2.Інженерна графіка: Довідник / В.М. Богданов, А.П. Верхола, Б.Д. Коваленко та ін.; За ред. А.П. Верхоли. – К.: Техніка, 2001. – 268 с.

3.В. О. Гордон, М. А. Семенцов – Огиевский. Курс начертательной геометрии. Учеб. пособие /Под ред. Ю. Б. Иванова. – 23-е изд., перераб. – М.: Наука. Гл. ред. физ. – мат. лит., 1988. – 272 с.: ил.

4.А.В. Бубенников. Начертательная геометрия. М., 1985

60