§ 3. Точечные оценки

3.1Определение оценки и ее качество

Дана выборка генеральной случайной величины Х. Обозначим через числовую характеристику или параметр, связанный со случайной величиной Х. По данным выборки требуется найти приближенное значение . Определяется функция от выборочных значений. Эта функция называется оценкой. В известном смысле значения оценки должны быть близки к значению

Качество оценки определяется не по одной выборке, а по всему мыслимому набору выборок, то есть по случайной выборке Поэтому оценка является случайной величиной.

По разным выборкам мы будем получать различные значения оценки , но в среднем эти значения должны быть равны величине

Оценка называется несмещенной, если ее математическое ожидание равно истинному значению:

Чем больше объем выборки, тем оценка должна лучше оценивать истинное значение Чаще всего отклонение значений оценки от истинного значения должно быть мало при больших объемах выборки.

Оценка называется состоятельной, если при увеличении объема выборки вероятность того, что оценка мало отличается от истинного значения, приближается к единице. Запишем это в виде предельного соотношения:

, для любого

Разброс значений случайной величины будет тем меньше, чем меньше ее дисперсия. Нам бы хотелось, чтобы разброс значений оценки был минимальным.

Несмещенная оценка называется эффективной, если она имеет наименьшую дисперсию среди всех несмещенных оценок данной истинной величины.

3.2 Оценки моментов

В математической статистике моменты генеральной случайной величины Х называются еще теоретическими моментами. Напомним их определение.

Центральный момент k-го порядка:

Начальный момент k-го порядка:

Центральные моменты выражаются через начальные.

В роли величины выступает момент. При построении оценки используется обобщенная выборочная случайная величина построенная по выборке:

				,

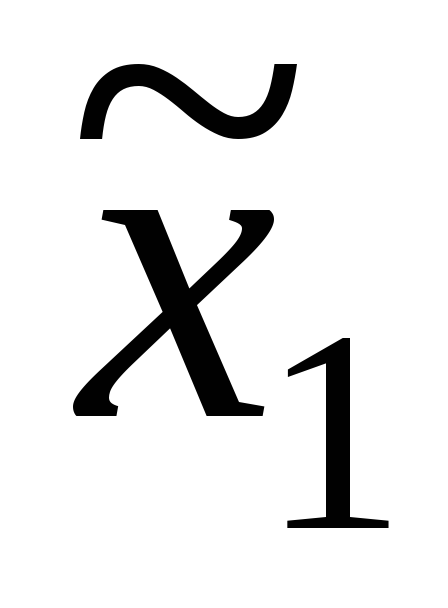
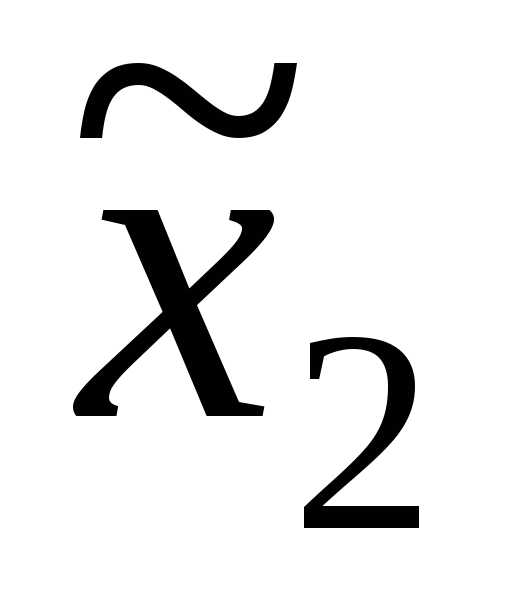
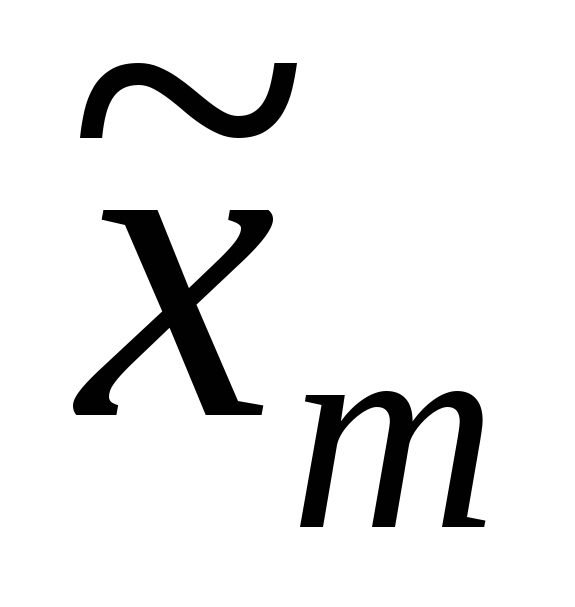
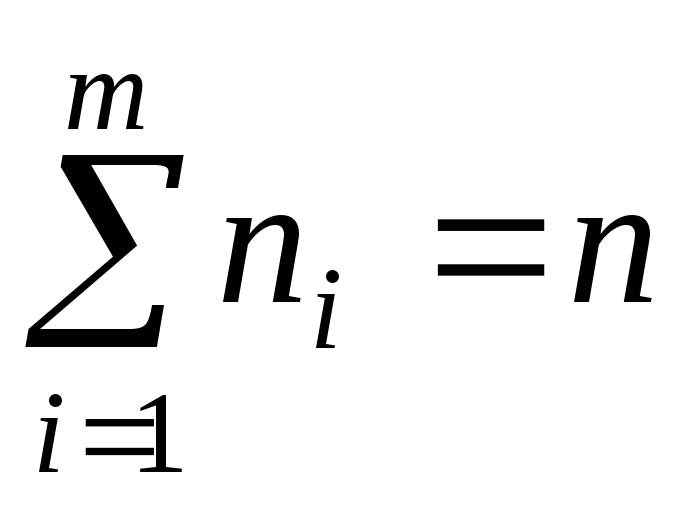
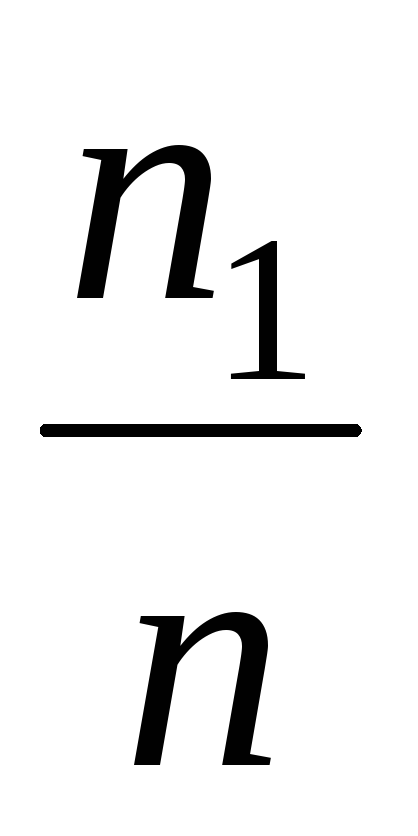
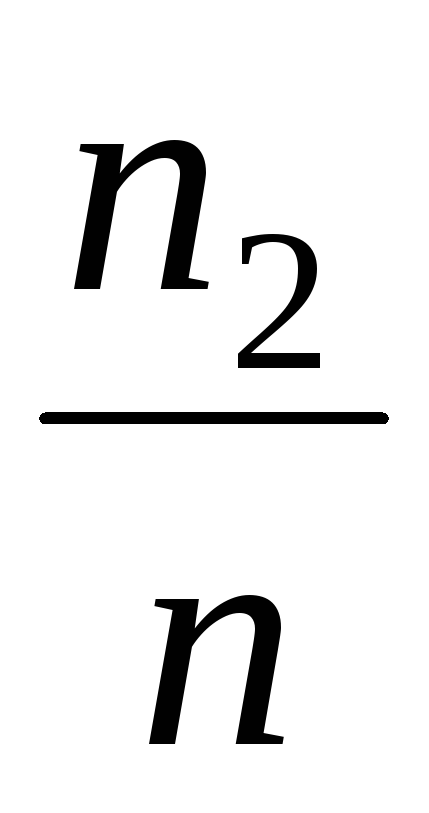
Выборочная случайная величина является дискретной. Начальный момент k-го порядка случайной величины

По необработанной выборке имеем:

Введем обозначение:

Согласно теореме Чебышева [2, §6], имеем:

для любого

Поэтому если истинная величина то в роли ее оценки будем брать то есть Оценка обозначается она еще называется выборочным (эмпирическим) моментом k-го порядка. Эти оценки являются состоятельными.

Аналогично вводятся и оценки центральных моментов:

Для необработанной выборки

Эти оценки также являются состоятельными. Из свойств математического ожидания вытекает несмещенность оценок начальных моментов:

Выборочные центральные моменты являются смещенными. Докажем смещенность выборочной дисперсии (центрального момента второго порядка). Для выборочной дисперсии вводится специальное обозначение:

Мы рассматриваем эту оценку как случайную величину. Раскроем квадрат под знаком суммы:

Найдем математическое ожидание каждого из слагаемых:

Тогда

Оценка корректируется с целью получения несмещенной оценки:

Несмещенная оценка дисперсии:

Пример 1. По выборке 2, 3, 2, 5, 3, 2 найти оценку математического ожидания (выборочное математическое ожидание).

Объем выборки п равен 6.

Найдем сумму всех выборочных значений:

Находим оценку математического ожидания:

Пример 2. По выборке найти несмещенную оценку дисперсии:

	0	2	3	5
	10	14	15	11

Объем выборки равен

Найдем оценку математического ожидания:

Найдем сумму квадратов отклонений от выборочного математического ожидания:

Находим несмещенную оценку дисперсии:

Можно считать, что где Х – генеральная случайная величина.