
- •Часть II Математическая статистика введение
- •§ 1. Задачи статистики. Понятие выборки
- •§ 2. Первичная обработка данных. Способы задания выборки. Эмпирический закон распределения
- •0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1.
- •§ 3. Точечные оценки
- •3.1Определение оценки и ее качество
- •3.2 Оценки моментов
- •3.3 Оценка функции распределения (эмпирическая функция распределения)
- •3.4 Оценка плотности распределения (гистограмма)
- •§ 4. Точечные оценки параметров распределения
- •4.1 Метод моментов
- •4.2 Метод максимального (наибольшего) правдоподобия
- •§ 5. Понятие интервальной оценки
- •5.1 Основные понятия
- •5.2 Доверительные интервалы для параметров нормального распределения
- •5.2.1Интервальные оценки для математического ожидания при известной дисперсии
- •5.2.2 Интервальные оценки математического ожидания при неизвестной дисперсии
- •5.2.3 Интервальные оценки дисперсии (среднеквадратического отклонения) при известном математическом ожидании
- •5.2.4 Интервальные оценки дисперсии (среднеквдратического отклонения) при неизвестном математическом ожидании
- •§ 6. Проверка статистических гипотез
- •6.1 Основные понятия
- •6.2 Гипотезы о математическом ожидании нормально распределенной генеральной случайной величины
- •6.3 Критерии согласия для предполагаемого закона распределения
- •6.3.1 Критерий согласия (критерий Пирсона)
- •6.3.2 Критерий Колмогорова
6.3 Критерии согласия для предполагаемого закона распределения
Не всегда есть
основания высказывать альтернативную
гипотезу ![]() в явном виде. Тогда выдвигается основная
гипотеза
в явном виде. Тогда выдвигается основная
гипотеза ![]() а конкурирующая гипотеза содержит
отрицание
а конкурирующая гипотеза содержит
отрицание ![]() Например:
Например:
![]() выборки двух
генеральных случайных величин, имеющих
равные дисперсии;
выборки двух
генеральных случайных величин, имеющих
равные дисперсии;
![]() выборки двух
случайных величин, имеющих не равные
дисперсии.
выборки двух
случайных величин, имеющих не равные
дисперсии.
В этом случае
проверка гипотезы состоит в выявлении
того, согласуется ли высказанное в
гипотезе ![]() предложение с выборочными наблюдениями
предложение с выборочными наблюдениями
![]() Такие критерии называются критериями
согласия.
Такие критерии называются критериями
согласия.
Рассмотрим основные гипотезы относительно закона распределения:
![]() выборка извлечена
из совокупности, имеющей распределение
с функцией
выборка извлечена
из совокупности, имеющей распределение
с функцией ![]()
Причем параметры
![]() могут быть указаны все или только
некоторые из них. Вместо функции
распределения может быть указан вид
закона распределения или плотность.
могут быть указаны все или только
некоторые из них. Вместо функции
распределения может быть указан вид
закона распределения или плотность.
Рассмотрим критерий
согласия ![]() и критерий Колмогорова.
и критерий Колмогорова.
6.3.1 Критерий согласия (критерий Пирсона)
Пусть ![]() выборка случайной величины Х.
На основе обработки данных мы можем
выдвинуть предположения о функции
распределения генеральной случайной
величины. Например, после построения
гистограммы проводится сравнение с
общими видами графиков плотностей
распределения известных законов. Если
высоты прямоугольников
выборка случайной величины Х.
На основе обработки данных мы можем
выдвинуть предположения о функции
распределения генеральной случайной
величины. Например, после построения
гистограммы проводится сравнение с
общими видами графиков плотностей
распределения известных законов. Если
высоты прямоугольников ![]() приблизительно одинаковые, то можно
предположить, что генеральная случайная
величина распределена равномерно.
приблизительно одинаковые, то можно
предположить, что генеральная случайная
величина распределена равномерно.
Итак, с заданным
уровнем значимости ![]() нужно проверить гипотезу
нужно проверить гипотезу ![]() генеральная совокупность имеет функцию
распределения
генеральная совокупность имеет функцию
распределения ![]()
Определим этапы проверки гипотезы:
1 этап. Разобьем
промежуток изменения выборочных данных
на r
интервалов ![]() без общих точек. Число членов выборки,
попавших в i-ый
интервал, обозначим
без общих точек. Число членов выборки,
попавших в i-ый
интервал, обозначим ![]() Величина
Величина ![]() показывает эмпирическую
вероятность попадания в i-ый
интервал.
Значение
показывает эмпирическую
вероятность попадания в i-ый
интервал.
Значение ![]() называют еще эмпирической частотой
попадания в i-ый
интервал.
называют еще эмпирической частотой
попадания в i-ый
интервал.
2 этап. Предположив
справедливость гипотезы ![]() вычисляем теоретическую вероятность
попадания в i-ый
интервал:
вычисляем теоретическую вероятность
попадания в i-ый
интервал: ![]() При подсчете теоретических вероятностей
есть определенные правила:
При подсчете теоретических вероятностей
есть определенные правила:
а)
В гипотезе ![]() указан вид распределения, но не все
параметры указаны. Пусть неизвестные
параметры
указан вид распределения, но не все
параметры указаны. Пусть неизвестные
параметры ![]() Далее сохраним обозначение s
– число оцененных параметров. В роли
значений параметров выступают их оценки
Далее сохраним обозначение s
– число оцененных параметров. В роли
значений параметров выступают их оценки
![]() (заметим, что в роли оценок не всегда
выступают оценки, приведенные в §4).
(заметим, что в роли оценок не всегда
выступают оценки, приведенные в §4).
б)
Объединение интервалов разбиения должно
покрывать всё множество значений
генеральной случайной величины: ![]() В противном случае проводится корректировка
первого и последнего интервалов
В противном случае проводится корректировка
первого и последнего интервалов ![]()
3 этап. Находятся
теоретические
частоты
![]() Если для некоторых интервалов
Если для некоторых интервалов ![]() то их объединяют с соседними так, чтобы
в итоге для каждого интервала теоретическая
частота была больше 5. При объединении
интервалов их эмпирические частоты
складываются. Новое число интервалов
обозначается
то их объединяют с соседними так, чтобы
в итоге для каждого интервала теоретическая
частота была больше 5. При объединении
интервалов их эмпирические частоты
складываются. Новое число интервалов
обозначается ![]()
4 этап. За меру отклонения выборки от гипотетического распределения принимают:
-
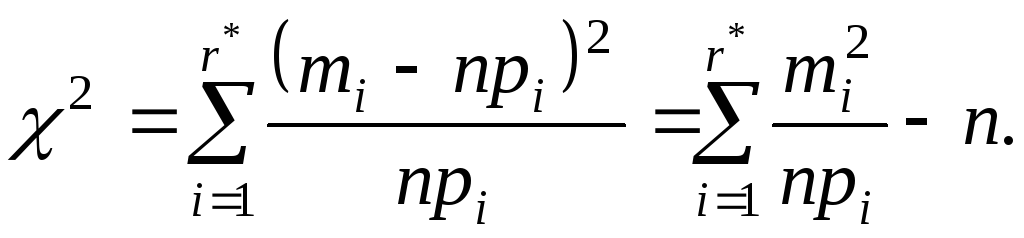
(6.3.1)
Значение критерия
![]() вычисленное по выборочным данным,
обозначим
вычисленное по выборочным данным,
обозначим ![]()
5 этап. При
выполнении гипотезы ![]() выборочным распределением
выборочным распределением ![]() будет
будет ![]() распределение с
распределение с ![]() степенью свободы. Для нахождения
критической точки используем таблицу
3: по
степенью свободы. Для нахождения
критической точки используем таблицу
3: по ![]() и
и ![]() находим
находим ![]() .
Критической областью является
.
Критической областью является ![]()
6 этап. Если
![]() то принимаем гипотезу
то принимаем гипотезу![]() Конечно, абсолютно истинной гипотезу
Конечно, абсолютно истинной гипотезу![]() не считаем.
не считаем.
Если
![]() то гипотезу
то гипотезу![]() отвергаем.
отвергаем.
Пример 1.
Даны эмпирические и теоретические
частоты попадания в каждый интервал
разбиения. Используя критерий ![]() при уровне значимости 0,05 проверить
гипотезу о нормальном распределении
генеральной случайной величины Х.
при уровне значимости 0,05 проверить
гипотезу о нормальном распределении
генеральной случайной величины Х.
-
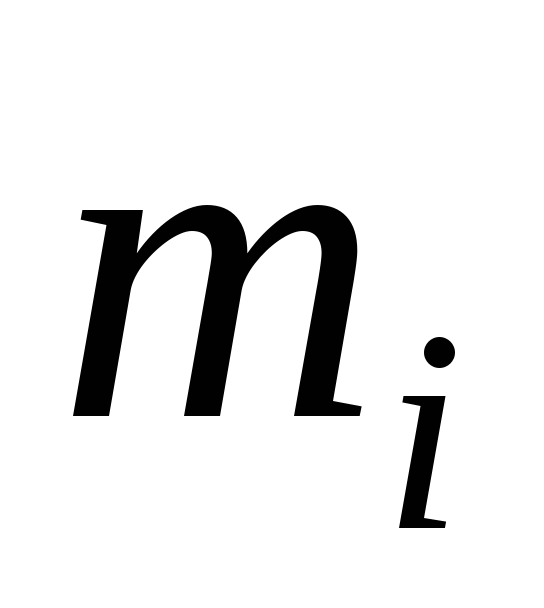
5
10
20
8
7
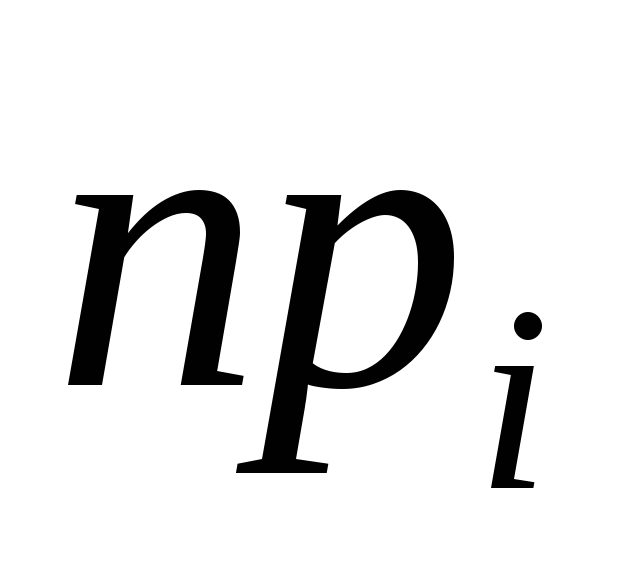
6
14
18
7
5
Здесь подсчет
теоретических и эмпирических частот
произведен. Гипотеза ![]() генеральная совокупность нормально
распределена. Тогда число оцененных
параметров
генеральная совокупность нормально
распределена. Тогда число оцененных
параметров ![]() Оценки параметров а
и
Оценки параметров а
и ![]() заранее вычислены, и с их использованием
найдены
заранее вычислены, и с их использованием
найдены ![]() Число интервалов
Число интервалов ![]() Объем выборки
Объем выборки ![]()
Найдем ![]()
![]()
![]()
![]()
Определим критическую
точку. Используем таблицу 3: при ![]() и числе степеней свободы
и числе степеней свободы ![]() имеем
имеем ![]()
Итак, ![]() и
и ![]() тогда
тогда ![]() и нет оснований отвергать гипотезу о
нормальном распределении генеральной
совокупности принимаем.
и нет оснований отвергать гипотезу о
нормальном распределении генеральной
совокупности принимаем.
Пример 2. Дан интервальный вариационный ряд (выборка задана интервально).
-
Интервалы

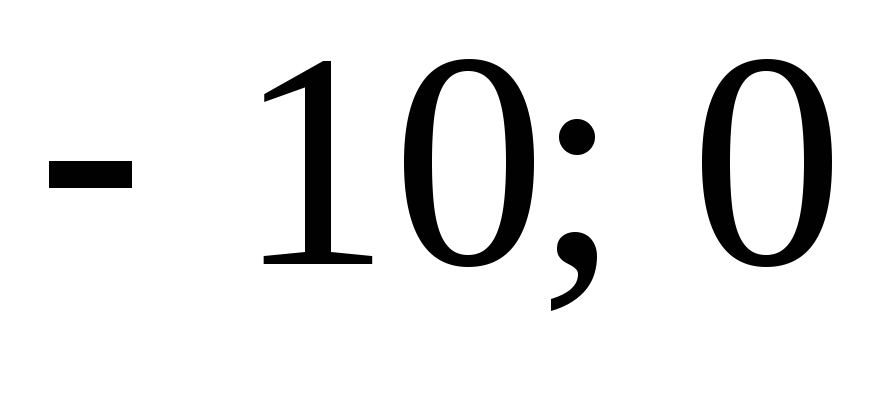
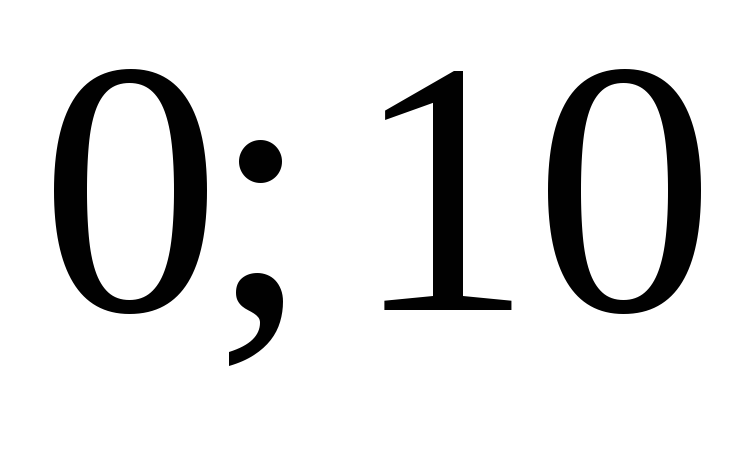
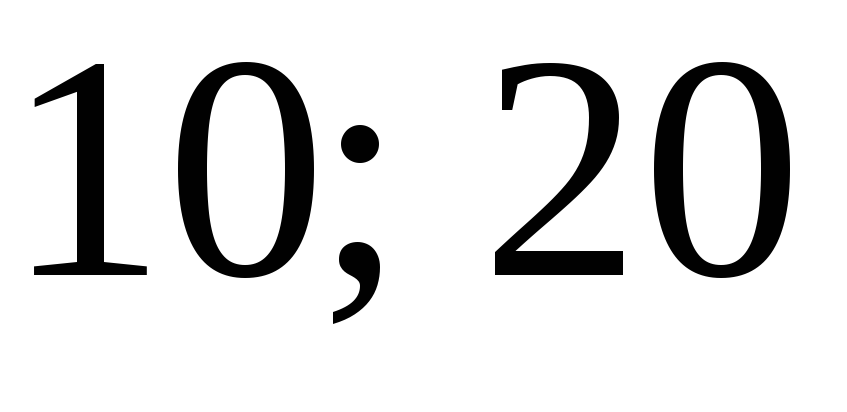
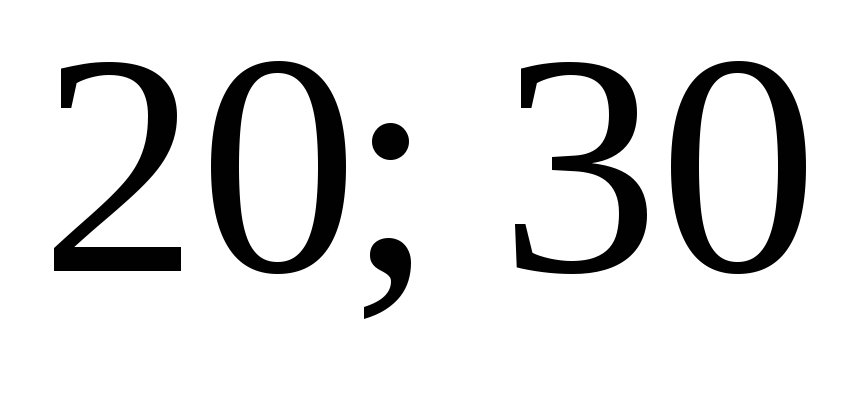
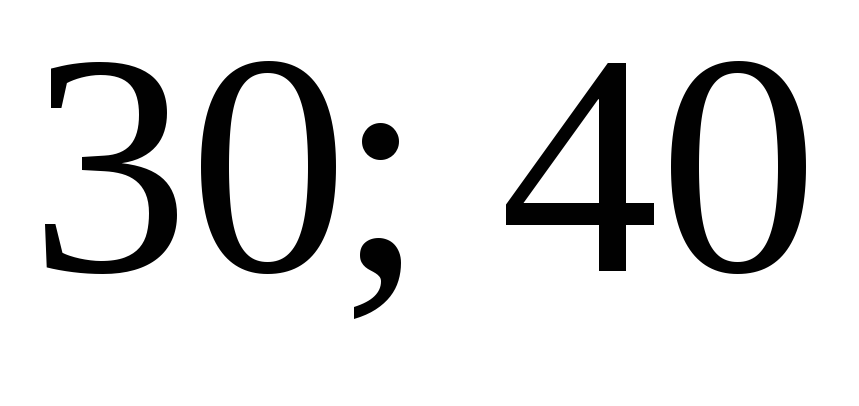
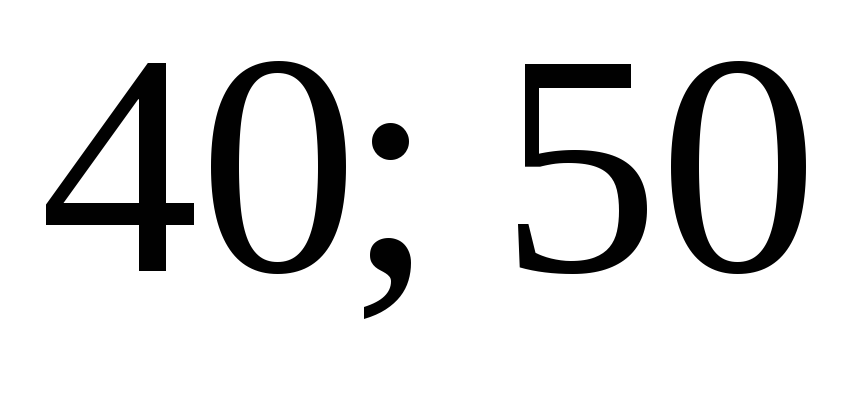
Частота
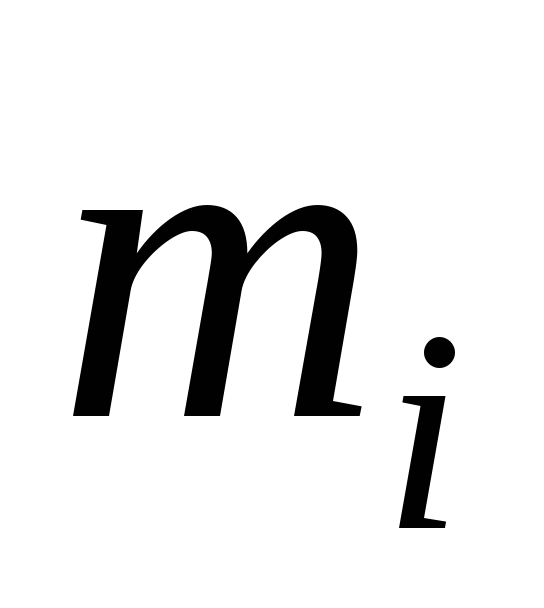
20
46
80
89
40
16
9
Гипотетическим является нормальное распределение.
При уровне значимости
![]() проверить, согласуется ли гипотеза о
нормальном распределении генеральной
случайной величины Х
с выборкой.
проверить, согласуется ли гипотеза о
нормальном распределении генеральной
случайной величины Х
с выборкой.
Объем выборки ![]()
Нужно оценить
параметры распределения. За выборочные
данные возьмем ![]() середины
интервалов.
середины
интервалов.
-
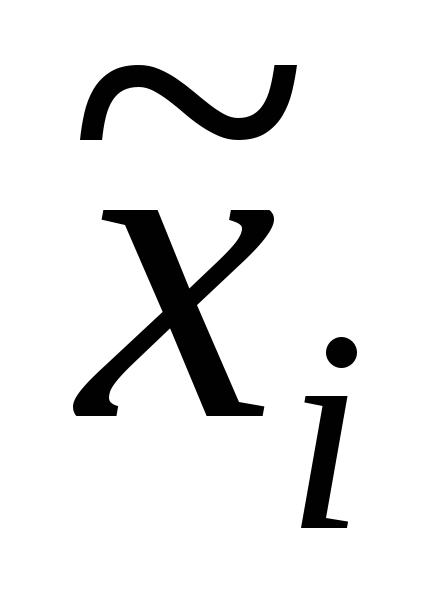
-15
-5
5
15
25
35
45
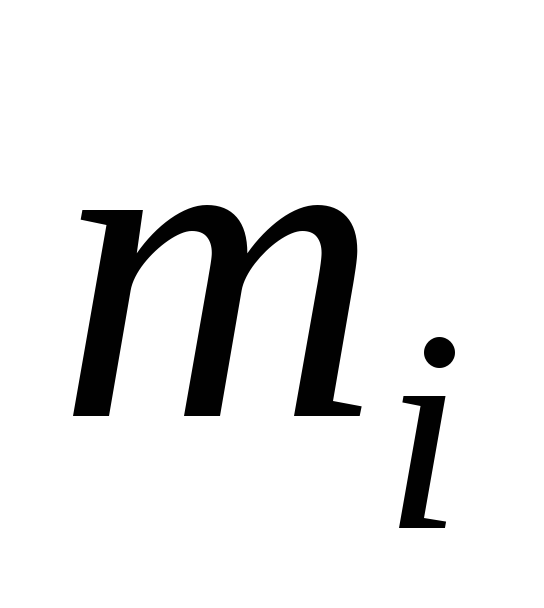
20
46
80
89
40
16
9
Найдем оценку математического ожидания:
![]()
Оценка параметра
а:
![]()
Вычислим несмещенную оценку дисперсии:
![]()
Оценка среднеквадратического отклонения:
![]()
Производится
подсчет теоретических попаданий в
каждый из интервалов. Используется
выражение ![]() функции
распределения нормального закона с
параметрами
функции
распределения нормального закона с
параметрами ![]() через
через ![]() функцию
Лапласа:
функцию
Лапласа:
![]() при
при ![]()
![]() при
при ![]()
Считается, что параметры равны их оценкам:
![]()
Нормально
распределенная случайная величина
принимает любое значение на числовой
оси. Поэтому при подсчете теоретических
вероятностей изменяется первый и
последний интервалы: первый интервал
![]() и последний
и последний ![]()
Находим теоретические вероятности:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Проведем проверку вычислений:
![]()
![]()
Занесем в таблицу
![]() эмпирические
частоты,
эмпирические
частоты, ![]() теоретические
вероятности и
теоретические
вероятности и ![]() теоретические
частоты с объемом выборки
теоретические
частоты с объемом выборки ![]()
-
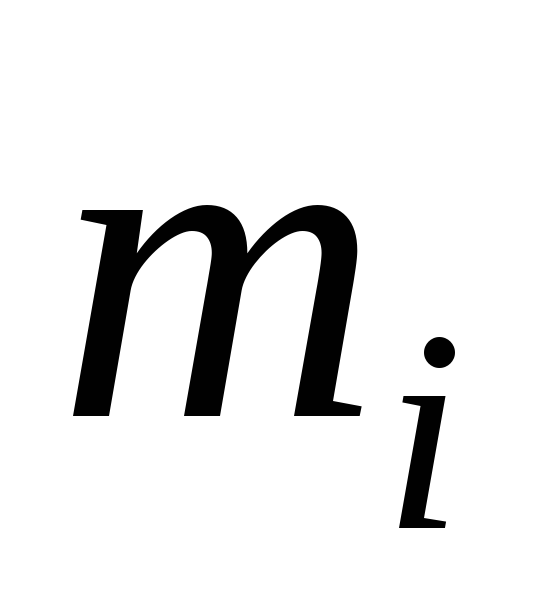
20
46
80
89
40
16
9
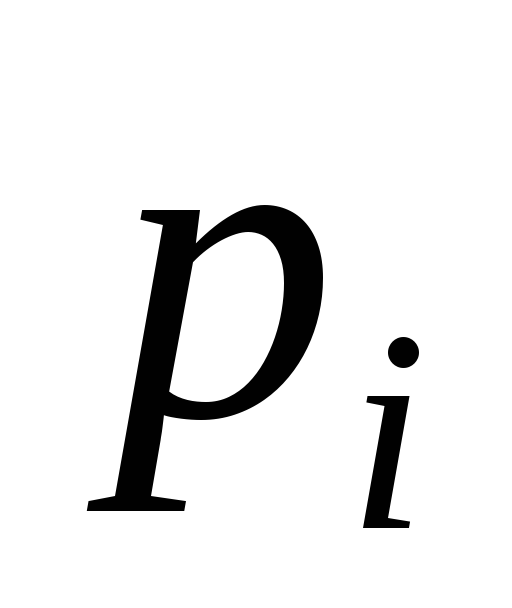
0,0688
0,1431
0,2682
0,2779
0,1686
0,0576
0,0158

20,64
42,93
80,46
83,37
50,58
17,28
4,74
В последнем интервале теоретическая частота меньше пяти:
![]()
Объединяем последний
интервал с предпоследним: в множество
![]() попало
попало ![]() членов выборки, теоретическая частота
попадания генеральной случайной величины
на
членов выборки, теоретическая частота
попадания генеральной случайной величины
на ![]() равна:
равна:
![]()
Число интервалов
после объединения ![]()
По формуле (6.3.1)
найдем ![]()
![]()
![]()
![]()
По таблице 3 найдем
критическую точку ![]() Подсчитаем число степеней свободы.
После объединения осталось 6 интервалов;
находились оценки двух параметров. При
Подсчитаем число степеней свободы.
После объединения осталось 6 интервалов;
находились оценки двух параметров. При
![]() и числе степеней свободы
и числе степеней свободы ![]() определяем
определяем ![]() Критической областью является
Критической областью является ![]()
Значение ![]() не превосходит
не превосходит ![]() Поэтому нет оснований отвергать гипотезу
Поэтому нет оснований отвергать гипотезу
![]() ,
то есть данные выборочные наблюдения
согласуются с гипотезой о нормальном
распределении генеральной случайной
величины Х.
,
то есть данные выборочные наблюдения
согласуются с гипотезой о нормальном
распределении генеральной случайной
величины Х.
Пример 3. Дана выборка генеральной случайной величины Х:
-

3
5
7
9
11
13
15
17
19
21

21
16
15
25
23
14
21
22
18
25
Используя критерий
![]() при уровне значимости
при уровне значимости ![]() проверить гипотезу о том, что случайная
величина Х
равномерно распределена на множестве
проверить гипотезу о том, что случайная
величина Х
равномерно распределена на множестве
![]()
Объем выборки: ![]()
По предположению
множество всех значений генеральной
случайной величины находится на отрезке
![]() Разобьем этот отрезок так, чтобы в каждом
интервале находилось одно выборочное
значение.
Разобьем этот отрезок так, чтобы в каждом
интервале находилось одно выборочное
значение.
Выберем следующее разбиение:
![]()
Эмпирические
частоты ![]() попадания в эти интервалы совпадают с
попадания в эти интервалы совпадают с
![]()
Найдем теоретические
вероятности попадания в интервалы
разбиения. Если случайная величина
равномерно распределена на отрезке ![]() и выполняется условие
и выполняется условие ![]() то
то
![]()
Параметры
распределения даны: ![]() Тогда:
Тогда:
![]()
![]()
![]()
![]()
![]()
Проведем проверку:
![]() Значение 1 не получено из-за округлений
в вычислениях.
Значение 1 не получено из-за округлений
в вычислениях.
Занесем в таблицу
эмпирические частоты
![]() теоретические вероятности
теоретические вероятности![]() и теоретические частоты
и теоретические частоты![]() :
:
-
i
1
2
3
4
5
6
7
8
9
10
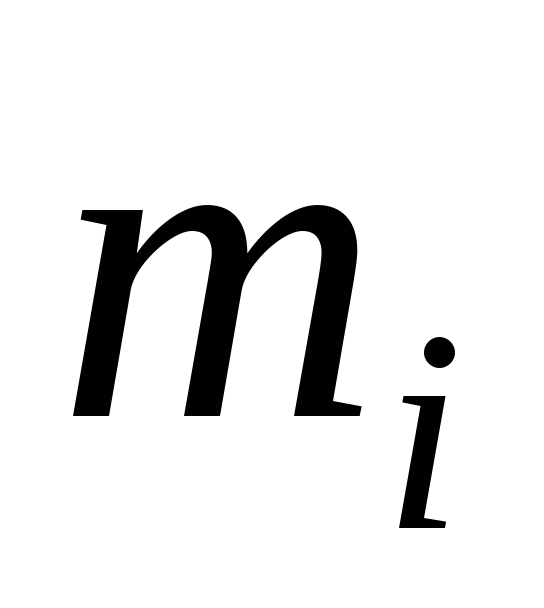
21
16
15
25
23
14
21
22
18
25
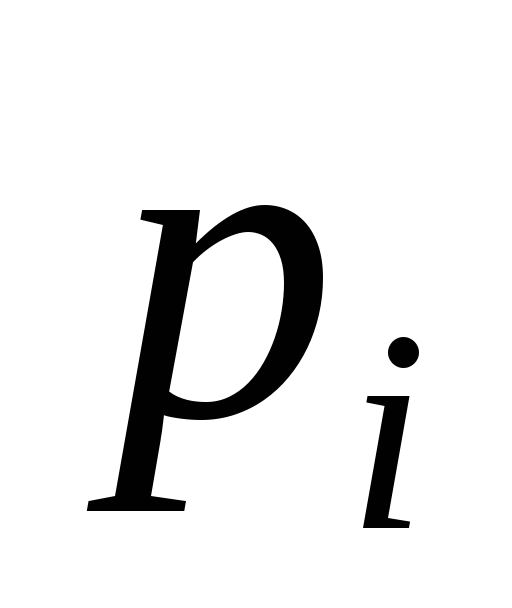
0,038
0,099
0,099
0,099
0,099
0,099
0,099
0,099
0,099
0,168

7,6
19,8
19,8
19,8
19,8
19,8
19,8
19,8
19,8
33,6
Все теоретические
частоты больше 5. Найдем наблюдаемое
значение критерия ![]() :
:
![]()
![]()
![]()
Определяется
критическая точка. В основной гипотезе
все параметры известны, поэтому число
оцененных параметров
![]() Всего 10 интервалов разбиения. Используем
таблицу 3: при
Всего 10 интервалов разбиения. Используем
таблицу 3: при![]() и числе степеней свободы
и числе степеней свободы![]() критическая точка:
критическая точка:![]() Критической областью является
Критической областью является![]()
Величина ![]() превышает
превышает
![]() Поэтому гипотеза о том, что случайная
величинаХ
распределена равномерно на
Поэтому гипотеза о том, что случайная
величинаХ
распределена равномерно на ![]() не согласуется с выборочными данными.
не согласуется с выборочными данными.
Пример 3. Одновременно подбрасывается четыре монеты, случайная величина Х показывает число выпадений герба. Приведена выборка генеральной случайной величины Х:
-
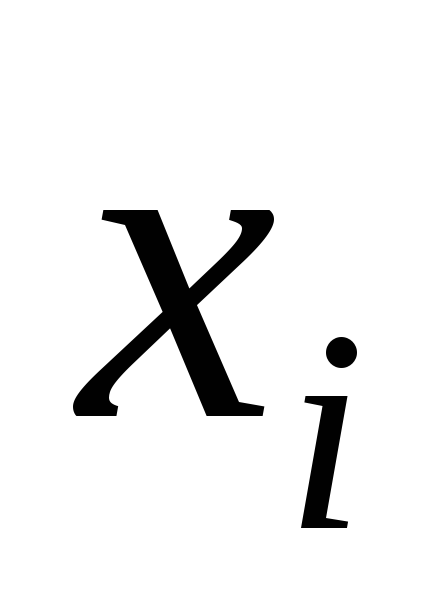
0
1
2
3
4

10
20
43
22
5
Используя критерий
![]() с уровнем значимости
с уровнем значимости![]() проверить гипотезу о том, что случайная
величинаХ
распределена по биномиальному закону.
проверить гипотезу о том, что случайная
величинаХ
распределена по биномиальному закону.
Объем выборки:
![]()
Параметрами
биномиального распределения являются
N
и р.
Число подбрасываемых монет равно 4,
поэтому
![]() Вероятность появления герба при
подбрасывании одной монеты неизвестна,
нужно оценить параметрр:
Вероятность появления герба при
подбрасывании одной монеты неизвестна,
нужно оценить параметрр:
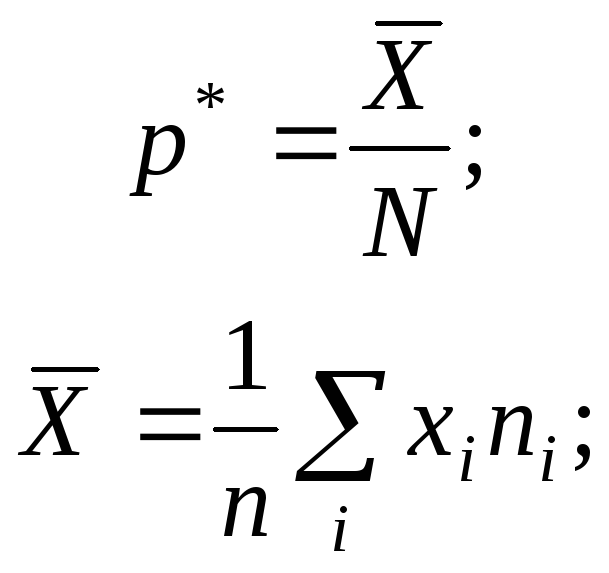
![]()
Множество выборочных
значений
![]() совпадает со множеством значений
случайной величиныХ.
Разбиваем отрезок
совпадает со множеством значений
случайной величиныХ.
Разбиваем отрезок
![]() на интервалы так, чтобы в каждый интервал
попало только одно выборочное значение:
на интервалы так, чтобы в каждый интервал
попало только одно выборочное значение:
![]()
Тогда:
![]()
Число интервалов
![]()
Используем формулу Бернулли:
![]()
Произведем
вычисление вероятностей
![]()
![]()
![]()
![]()
![]()
![]()
Занесем в таблицу
эмпирические частоты
![]() теоретические вероятности
теоретические вероятности![]() и теоретические частоты
и теоретические частоты![]() (объем выборки
(объем выборки![]() ).
).
-
i
1
2
3
4
5
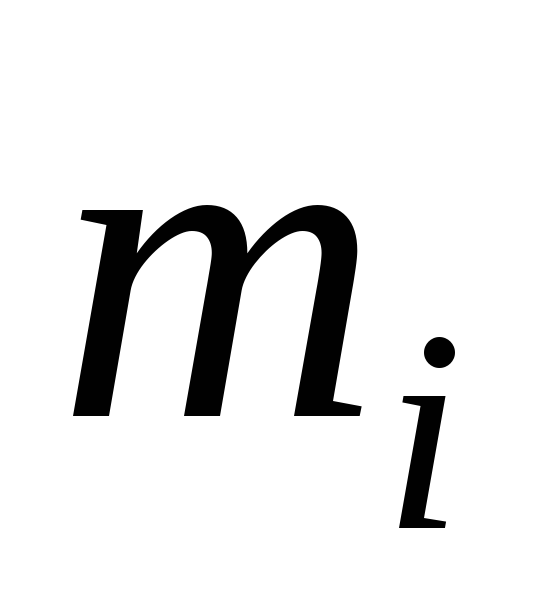
10
20
43
22
5
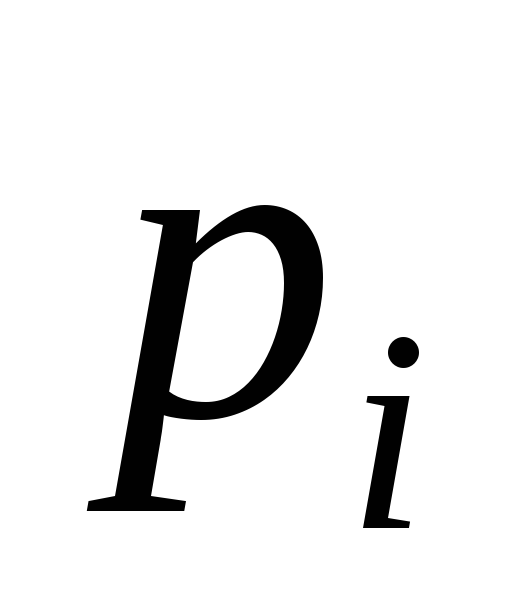
0,073
0,27
0,374
0,23
0,053
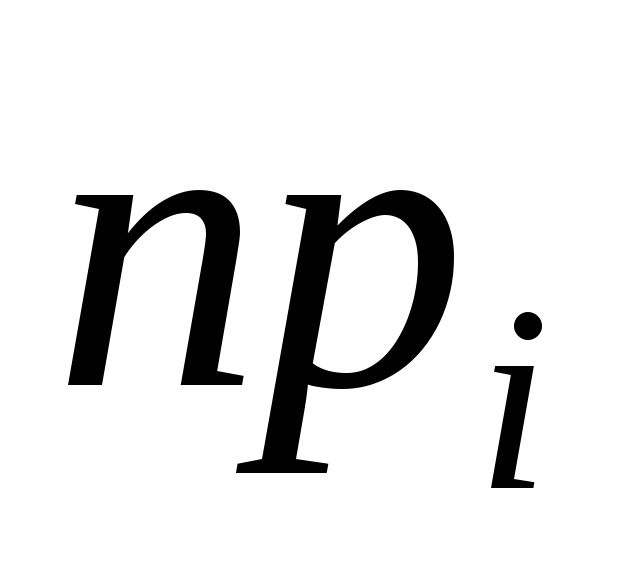
7,3
27
37,4
23
5,3
Все теоретические частоты больше 5.
Определим наблюдаемое значения критерия:
![]()
![]()
![]()
Находилась оценка
только одного параметра, поэтому
![]() Число выборочных значений равно числу
интервалов разбиения, поэтому
Число выборочных значений равно числу
интервалов разбиения, поэтому![]() Используем таблицу 3: при
Используем таблицу 3: при![]() и числе степеней свободы
и числе степеней свободы![]() определяем критическую точку
определяем критическую точку![]()
Наблюдаемое
значение критерия ![]() не превышает критическое значение
не превышает критическое значение
![]() Поэтому нет оснований отвергать гипотезу
о биномиальном распределении генеральной
случайной величиныХ.
Поэтому нет оснований отвергать гипотезу
о биномиальном распределении генеральной
случайной величиныХ.
