Диференціальні рівняння Латышев

Міністерство освіти і науки України

ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ АВТОМОБІЛЬНО-ДОРОЖНІЙ УНІВЕРСИТЕТ

МЕТОДИЧНІ ВКАЗІВКИ ТА ЗАВДАННЯ

до теми «Диференціальні рівняння»

Затверджено методичною радою університету протокол № 3 від 09.12.2010 р.

Харків

ХНАДУ

2010

Укладачі: Латишев В.Р. Небратенко О.В.

Кафедра вищої математики

Дані вказівки та завдання до самостійної роботи студентів інженерно-технічних та економічних спеціальностей складені у відповідності до діючих програм і охоплюють одну з найважливіших частин дисципліни «Вища математика», а саме «Диференціальні рівняння».

Мета даного видання – допомогти студентам у самостійній роботі по засвоєнню даного розділу.

Завдання для самостійної роботи розташовані в додатку. Кожне завдання має 18 прикладів і задач по кожній темі, що сприяє підвищенню якості індивідуальної роботи студентів. Завдання відображають такі теми:

•диференціальні рівняння першого порядку з відокремлюваними змінними, однорідні, лінійні і рівняння Бернуллі;

•диференціальні рівняння другого порядку, які допускають пониження порядку;

•лінійні однорідні і неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами;

•системи лінійних диференційних рівнянь із сталими коефіцієнтами.

3

1. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ПЕРШОГО ПОРЯДКУ

1.1. Загальні поняття та означення

Диференціальним рівнянням першого порядку називається рівняння виду

F(x, y, y′) = 0,

яке зв’язує незалежну змінну х, невідому функцію y=y(x) та її похідну y′.

Це рівняння може не містити явно x або y, але обов’язково має містити похідну y′ (у протилежному випадку воно не буде диференціальним).

Якщо рівняння можна розв’язати відносно y′, то його записують у вигляді

y′ = f (x, y)

і називають рівнянням першого порядку, розв’язаним відносно похідної. Загальним розв’язком диференціального рівняння в області G називається функція y=φ(x,с), яка залежить від аргументу

хі довільної сталої С, якщо вона задовольняє дві умови:

1)функція φ(x,с) є розв’язком рівняння при будь-якому значенні сталої С;

2)для довільної точки (x0,y0) є G можна знайти таке значення C=C0, що функція y=φ(x,с0),задовольняє початкову умову:

φ(x0 ,с0 ) = y0 .

Частинним розв’язком рівняння називається функція y=φ(x,с0), яка утворюється із загального розв’язку y=φ(x,с) при певному значенні сталої С=С0.

Якщо загальний розв’язок диференціального рівняння знайдено в неявному вигляді Ф (x,y,c) = 0, то такий розв’язок називають загальним інтегралом диференціального рівняння.

4

Рівність Ф(x,y,c0) = 0 у цьому випадку називають частинним інтегралом рівняння.

1.2.Диференціальні рівняння

звідокремлюваними змінними

Рівняння, яке можна звести до вигляду y′ = f (x) φ( y) ,

де f(x) і φ(y) – задані і неперервні на деякому інтервалі функції, називається диференціальним рівнянням з відокремлюваними змінними.

Щоб розв’язати рівняння треба замінити y′ на dydx , поділити обидві частини рівняння на φ( y) ≠ 0 і помножити на dx, тоді рівняння залишиться у вигляді φdy( y) = f (x) dx.

Оскільки рівняння містить тотожні рівні диференціали, то відповідні невизначені інтеграли відрізняються між собою на сталу величину, тобто

. ∫ φdy( y) = ∫ f (x) dx +c ..

Приклади.

1. Розв’язати рівняння:

(х+ xy2 )dx −(y + yx2 )dx = 0.

Розв’язання.

Оскільки це рівняння можна записати у вигляді x(1+ y2 )dx − y(1+ x2 )dy = 0,

5

то воно є рівнянням з відокремлюваними змінними. Поділивши обидві його частини на (1+ x2 )(1+ y2 )≠ 0 , дістанемо рівняння з відокремленими змінними:

x	dx −	y	= 0 або	2xdx	=		2 ydy	.
1+ х2		1+ y2		1+ х2
						1+ y2

Інтегруючи останнє рівняння, маємо:

ln	1+ x2	= ln	1+ y2	+ln		с		,	с ≠ 0.

Потенціюючи, дістаємо загальний інтеграл рівняння:

1+ x2 = с(1+ y2 ),

с ≠ 0 .

2. Знайти частинний розв’язок рівняння:

(1+ x2 )dy + ydx = 0,

який задовольняє початкову умову y(0)=1.

Розв’язання.

Відокремимо змінні і проінтегруємо дане рівняння:

dy

+

dx

= 0;

∫

dy

+ ∫

dx

= с;

ln

y

+ arctg x = c .

y

1+ x2

y

1+ x2

Дістали загальний інтеграл.

Використовуючи початкову умову, знайдемо С: ln1+arсtg y 0 = с,звідки с = 0.

Підставивши знайдемо сталу в загальний інтеграл, дістанемо шуканий частинний інтеграл:

ln y +arctg x = 0,звідки y =e arctg x частинний розв’язок.

6

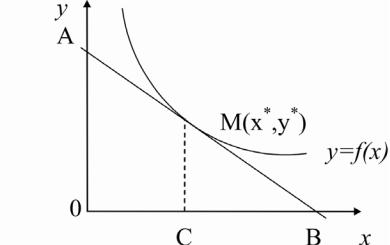
3. Знайти криву, яка проходить через точку М0(1;2), коли відомо, що у кожній точці кривої відрізок дотичної, який міститься між осями координат, ділиться точкою дотику навпіл.

Розв’язання.

Нехай М(x*,y*) – довільна точка шуканої кривої y=f(x).

Запишемо рівняння дотичної, проведеноїдоцієїкривоївточціМ:

y − y* = y′(x* ) (x − x* ),

де (x*,y*) – довільна точка дотичної (дивись малюнок).

Оскільки за умовою АМ=ВМ, то ОС=ВС, звідки ОВ=2ОС=2х*. У точці В дотична перетинає вісь ох, тому з рівняння дотичної при y = 0 дістанемо абсцису х точки В:

x = x* −

y*

.

′

*

)

y (x

Дістаємо рівняння x* −

y*

= 2x* або

y′

= −

1

.

′

*

)

y

x

y (x

Тому що М(x*,y*) взята довільно, то замінили x*, y* на x і y відповідно.

Відокремлюємо змінні і проінтегруємо останнє рівняння:

y

′

y

dy

y

dy

dx

= − x

;

dx = − x ;

y = − x ;

7

∫

dy

= −∫

dx

+ln

с

;

ln

y

= ln

с

;

y

x

x

y = cx – загальний розв’язок.

За умовою y(1) = 2, знаходимо с = 2, тому y = 2x – рівняння шуканої кривої.

1.3. Однорідні диференціальні рівняння

Диференціальне рівняння y′ = f (x, y) називається однорідним,

якщо функцію f (x, y) можна записати у вигляді φ xy , тобто

y′ = φ

y

,

а це можливо,

якщо функція

f (x, y) є

однорідною

x

функцією нульового виміру.

Зауваження.

називається однорідною функцією n-го виміру

Функція f (x, y)

відносно

змінних

x

та

y,

якщо для

довільного

числа t ≠ 0

виконується тотожність:

f (tx,ty) = tn f (x, y) .

Наприклад, функція

f (x, y) = x2 −2xy

– однорідна функція

другого виміру, оскільки

f (tx,ty) = (tx)2 −2(tx) (ty) = t2 (x2 −2xy) = t2 f (x, y) ,

а функція

f (x, y) =

2x −3y

– однорідна функція нульового виміру,

x + 2 y

оскільки

2(tx) −3(ty)

t(2x −3y)

2x −3y

f (tx,ty) =

=

= t0

= t0

f (x, y) .

tx + 2(ty)

t(x + 2 y)

x + 2y

8

Покажемо, що однорідні рівняння зводяться до рівнянь з відокремлюваними змінними підстановкою

u =

y

,

x

де u = u(x) – невідома функція.

Якщо

функція

y =u x

є

розв’язком

диференціального

рівняння і

y

′

′

′

′

′

+u =φ(u) . Відокремлюючи

= u x +ux

= u x +u , то

u x

змінні, дістаємо рівняння:

du

−u =

dx

.

φ(u)

x

Проінтегрувавши знайдемо:

∫

du

= ∫

dx

+ln

с

або

∫

du

= ln

cx

.

φ(u) −u

x

φ(u) −u

y

Підставимо

після

інтегрування замість u

відношення

і

x

дістанемо загальний інтеграл рівняння.

Приклад.

1. Розв’язати рівняння:

y′ =

x2 + y2

.

2x2

Розв’язання.

Якщо поділити чисельник і знаменник правої частини рівняння

y 2

2

1+

y

′

x

на x ≠ 0 ,

то будемо мати рівняння

=

, яке

є

y

2

однорідним.

Застосувавши підстановку

u

=

,

а

y =u x

і

x

y′ = ux′+u , дістанемо загальний інтеграл даного рівняння:

9

′

1+u2

′

1+u2

du

(u −1)2

u x +u =

;

u x =

−u;

x

=

;

2

2

dx

2

2du

=

dx

;

∫

2du

= ∫

dx

+ln

с

;

(u −1)2

(u −1)2

x

x

2

2

2x

−

= ln

сx

;

−

= ln

сx

;

= ln

сx

;

u −1

y

−1

x − y

x

2 x

Відповідь: cx = ex−y .

1.4. Лінійні диференціальні рівняння

Лінійним диференціальним рівнянням першого порядку називається рівняння виду:

y′+ρ(x) y = q(x),

де ρ(x) і q(x) – задані і неперервні на деякому проміжку функції.

Розв’язок цього рівняння шукають за методом підстановки у вигляді добутку y = u ϑ, де u = u(x), ϑ = ϑ(x) – невідомі функції,

причому одна з цих функцій довільна (але не рівна тотожно нулю).

Приклади.

1. Знайти загальний розв’язок рівняння:

y′

+

y

=

sin 2x

.

x

x

Розв’язання.

1

sin 2x

Це лінійне

рівняння в

якому ρ(x) =

,

q(x) =

.

Нехай

x

y = u ϑ, тоді y

′

′

′

x

= u ϑ+uϑ. Маємо:

′

′

uϑ

sin 2x

′

′

ϑ

sin 2x

u ϑ+uϑ +

=

;

u ϑ+u(ϑ + x ) =

.

x

x

x

10