архив прош.сесий / архив прош.сесий / L_3_2014_MMS_Bazova

1

ДЕРЖАВНИЙ УНІВЕРСИТЕТ ТЕЛЕКОМУНІКАЦІЙ

Кафедра вищої математики

ЗАТВЕРДЖУЮ Завідувач кафедри ______________

О. В. Барабаш "___" _____________20___ року

ЛЕКЦІЯ

з навчальної дисципліни

Математичні методи в соціології

Тема 1. Вступ до курсу “Математичні методи в соціології ”. Базовий матеріал до курсу із теорії ймовірностей: Випадкові величини одно-та двовимірні

Лекція 3. Базовий матеріал до курсу “Математичні методи в соціології ”із теорії ймовірно-

стей: Числові характеристики випадкових величин.

Навчальний час – 1,5 годин.

Для студентів Навчально-наукового інституту Гуманітарних технологій за напрямом підго-

товки 402 соціологія, освітньо-кваліфікаційного рівня бакалавр, спеціальністю 6.040201 ”соціологія

Навчальна та виховна мета: 1. Виведення формул розрахунку числових характеристик випадкової величини.

2. Навчити студентів застосувати отримані формули для розв’язання прикладів.

Обговорено та схвалено на засіданні кафедри “___” _________ 20___ року Протокол №____

Київ – 20__

2

Зміст

Вступ

1. Поняття незалежності випадкових величин. Закони розподілу суми, різниці, добутку не-

залежних випадкових величин.

2. Числові характеристики випадкової величини.

2.1. Характеристики положення: математичне очікування випадкової величини і його влас-

тивості; мода та медіана випадкової величини.

2.2.Характеристики розсіювання: дисперсія та середнє квадратичне відхилення випадкової величини, їхні властивості.

2.3.Початкові та центральні моменти випадкової величини. Характеристики форми: кое-

фіцієнти асиметрії та ексцесу Заключна частина.

Л I Т Е Р А Т У Р А

1. Барковський В.В., Барковська Н.В., Лопатін О.К. Теорія імовірностей та математична статистика. К.:ЦНЛ, – 2006 – 424 с.

Наочні посібники

Завдання на самостійну роботу

1.Вивчити матеріал лекції за підручником [1] (стор. 93-100) та наступним текстом лекції.

Вступ – в лекції розглядається базовий матеріал до курсу “Математичні методи в соціоло-

гії ”із теорії ймовірностей: Закони розподілу суми, різниці, добутку незалежних випадкових вели-

чин. Числові характеристики випадкових величин.

1. Поняття незалежності випадкових величин. Закони розподілу суми, різниці, добутку незалеж-

них випадкових величин Означення 1. Дві випадкові величини називають незалежними, якщо закон розподілу однієї

з них не змінюється від того, якого саме із своїх можливих значень набула інша величина.

Наприклад, якщо дискретна випадкова величина X може набувати значення хі (і=1,2, n),

а випадкова величина Y – значення уj (j=1,2, m), то незалежність випадкових величин X і Y озна-

чає незалежність подій X=хі й Y=уj (за будь-яких і=1,2, n та j=1,2, m). Інакше, випадкові вели-

чини називають залежними.

Дане визначення незалежності випадкових величин еквівалентне наступному, справедли-

вому як для дискретних так і для неперервних випадкових величин.

3

Означення 2. Випадкові величини X і Y називаються незалежними, якщо для всіх можли-

вих дійсних х, y справедлива рівність

			P ( X x) (Y y) P( X x) P(Y y) ,						(1)
тобто для всіх можливих дійсних х, y події ( X x) ; (Y y) – незалежні.
			Алгебраїчні операції над випадковими величинами
	Нехай дано дві дискретні випадкові величини X і Y у вигляді рядів розподілу:
X		х1		х2	…	хі		…	хn
Р		р1		р2	…	рі		…	рn
Y		у1		у2	…	уj		…	уm
Р		g1		g2	…	gj		…	gm

Означення 3. Сумою (різницею або добутком) дискретних випадкових величин X та Y на-

зивається випадкова величина, яка набуває всіх можливих значень вигляду хі+уj (хі уj або хі уj) (де

і=1,2, n; j=1,2, m) із імовірностями ріj того, що випадкова величина X набуде значення хі, а Y –

значення уj :
ріj=Р[(X=хі) (Y=уj)].	(2)
Якщо випадкові величини X та Y незалежні, тобто незалежними є події X=хі й Y=уj за будь
яких значень і=1,2, n; j=1,2, m, то за теоремою множення ймовірностей незалежних подій:
ріj=Р(X=хі) Р(Y=уj)=рі gj.	(3)
Із визначення добутку випадкових величин випливає наступне:

1) m–им степенем дискретної випадкової величини X, тобто Xт, називається випадкова величина, яка набуває значень хіт з тими самими ймовірностями рі, (i 1, 2,..., n) , що й сама вели-

чина X;

2) добутком kX дискретної випадкової величини X на сталу величину k називають випад-

кову величину, яка набуває значень kхі з тими самими ймовірностями рі, (i 1, 2,..., n) , що й сама величина X, оскільки сталу k можна розглядати як випадкову величину, що з імовірністю, яка до-

рівнює одиниці, набуває значення k.

Для суми та добутку випадкових величин, кількість яких більша двох і скінченна, мають місце переставний, сполучний та розподільний закони.

Означення 4. Дискретні випадкові величини Х1, Х2, , Хn називаються незалежними в суку-

пності, якщо закон розподілу кожної з них не змінюється від того, яких саме із їхніх можливих значень набувають всі інші випадкові величини чи випадкові величини довільної комбінації із до-

вільної кількості цих величин.

4

За побудови закону розподілу суми скажімо 3-х випадкових величин незалежних в сукуп-

ності, X+Y+Z, за теоремою множення ймовірностей незалежних в сукупності подій дістанемо:

ріjs=Р[(X=хі) (Y=уj) (Z=zs)]=Р(X=хі) Р(Y=уj) Р(Z=zs). (4)

Приклад 1. Задано закони розподілів двох незалежних випадкових величин X і Y:

					X								0				2				5
					Р								0,5				0,2				0,3
Y								-2						0				2				3
Р								0,1						0,2				0,4				0,3
		Знайти закони розподілів випадкових величин: а) U=3X; б) V=Y2;
		в) Z=X–Y.
		▼ а) Можливі значення випадкової величини U=3X будуть:
		U=3X				0				6			15						3 0;	3 2;	3 5
																	з тими самими ймовірностями,
																	що й для величини Х: 0,5; 0,3; 0,2.
		Р				0,5				0,3			0,2
			2														б) Можливі значення випадкової
		V=Y			0				4				9
																	величини V=Y2 будуть:
																							9 .
		Р			0,2				0,5				0,3				( 2)2 4,		02 0,	22	4, 32

Оскільки V=4 зустрічається двічі, то P(V 4) 0,1 0, 4 0,5 .

в) Ймовірності значень випадкової величини Z=X–Y отримуються множенням ймовірнос-

тей відповідних значень випадкових величин X та Y, оскільки ці величини незалежні. Наприклад,

якщо X=5, а Y=3, то випадкова величина Z=X–Y набуває значення Z=5-3=2 з ймовірністю:

P(Z 2) P(X 5) P(Y 3) 0,3 0,3 0, 09 .

Серед 12-ти можливих значень (3 4=12) є однакові:

Z=Х–Y=0: 0-0=0, 2-2=0;

Z=Х–Y=2: 0-(-2)=2, 2-0=2, 5-3=2.

Ймовірності однакових можливих значень додаємо:

Р(Z=0)=Р(Х=0) Р(Y=0)+Р(Х=2) Р(Y=2)=0,5 0,2+0,2 0,4=0,18;

Р(Z=2)=Р(Х=0) Р(Y= 2)+Р(Х=2) Р(Y=0)+Р(Х=5) Р(Y=3)=0,5 0,1+0,2 0,2+ +0,3 0,3=0,18.

Упорядковуючи можливі значення випадкової величини Х–Y в порядку зростання, отри-

маємо розподіл випадкової величини Z=Х–Y:

5

Z=Х–Y	-3	-2	-1	0	2	3	4	5	7
Р	0,15	0,2	0,06	0,18	0,18	0,12	0,02	0,06	0,03

9

Впевнимось, що pk 0,15 0, 2 0, 06 0,18 0,18 0,12 0, 02 0, 06 0, 03 1 .▲

k1

2.Числові характеристики випадкової величини. Моменти розподілу випадкової величини.

Функція розподілу ймовірностей повністю характеризує випадкову величину, проте вона часто є невідомою. На практиці немає потреби так докладно описувати випадкову величину, а

достатньо знати лише певні параметри, які несуть про неї істотну інформацію. Ці параметри є не-

випадковими числовими характеристики випадкової величини. Розлянемо найважливіші з них.

2.1. Характеристики положення: математичне очікування випадкової величини і його вла-

стивості; мода та медіана випадкової величини.

Математичне очікування

Означення 5. Математичним очікуванням випадкової величини Х, визначеної на просторі елементарних подій Ω, називають числову характеристику М(Х), яка виражає “середнє зважене за ймовірністю значення” випадкової величини, а саме:

якщо простір Ω дискретний, то математичне очікування M(X) визначається рівністю:

M ( X ) xi pi ,				(5)
	i 1
Нескінченна сума (5) повинна бути збіжною за модулем, тобто			xi		pi .
	i 1
У випадку обмеженого дискретного простору Ω
n
M ( X ) xi pi	=x1p1+x2p2+…+xnpn.			(6)

i 1

Отже, математичне очікування дискретної випадкової величини дорівнює сумі добут-

ків усіх її можливих значень на їхні ймовірності.

Математичне очікування неперервної випадкової величини вводиться у такий спосіб.

Нехай неперервна випадкова величина Х набуває значень з інтервалу [ ; ] і задана щіль-

ністю (густиною) розподілу f(x). Розіб’ємо інтервал на n елементарних проміжків: x1, x2 ,..., xn

і виберемо в кожному проміжку довільно точку хі (i 1, 2,..n) . Складемо суму добутків можливих

n

значень хі випадкової величини Х на ймовірності її попадання в проміжки хі, xi f (xi ) xi (до-

i 1

буток f(хі) хі приблизно рівний ймовірності попадання Х в інтервал хі). Перейшовши до границі в одержаному виразі, за прямування до нуля найбільшого з проміжків, отримаємо математичне очікування неперервної випадкової величини

6

β
M ( X ) x f (x)dx ,	(7)

α

Для математичного очікування неперервної випадкової величини, заданої на всій чис-

ловій осі, дістанемо

M ( X ) x f (x)dx ,	(8)

за умови абсолютної збіжності інтеграла.

Властивості математичного очікування

Математичне очікування має такі властивості:

1. На числовій осі можливі значення випадкової величини X розміщені зліва та справа від математичного очікування. Тому математичне очікування називають центром розподілу або

середнім значенням випадкової величини.

2. Математичне очікування від сталої величини С дорівнює самій сталій:

М(С)=С,

оскільки сталу С можна розглядати як випадкову величину, що з імовірністю, яка дорівнює оди-

ниці, набуває значення С, а тому М(С)=С1=С.

3. Сталий множник можна виносити за знак математичного очікування:

М(СХ)=СМ(Х),

	n	n
Справді,	M (CX ) (C xi ) pi	C xk pk CM ( X ) .
	i 1	i 1

4. Математичне очікування алгебраїчної суми двох незалежних випадкових величин дорів-

нює алгебраїчній сумі математичних очікувань цих величин:

М(Х Y)=М(Х) М(Y).

5. Математичне очікування добутку двох незалежних випадкових величин дорівнює добу-

тку їх математичних очікувань:

М(Х Y)=М(Х) М(Y).

6. Із застосуванням сполучного закону додавання та множення, для суми та добутку скін-

ченної кількості випадкових величин, кількість яких більша двох, на основі властивостей 4 та 5

дістанемо: математичне очікування суми (добутку) незалежних в сукупності випадкових величин дорівнює сумі (добутку) математичних очікувань цих величин.

Статистичний зміст математичного очікування

Нехай проведено n експериментів, в nі із яких (і=1,2k) випадкова величина Х набула зна-

чення хі (і=1,2k); отже, n1+n2+…+nk=n. Підрахуємо середнє арифметичне значення спостереже-

ної величини Х

7

M			n1x1 n2 x2 ... ni xi	x W	x W	... x W	x p	x p	... x p M (X ) .
	сер.арифм.
			n	1 1	1 2	i i	1 1	1 2	i i

Тут величини Wі=Wі(хі) – відносні частоти спостереженого значення хі випадкової величи-

ни Х, які наближено дорівнюють величині ймовірності події (Х=хі), рі Рі(Х=хі). Це обґрунтовуєть-

ся законом великих чисел за достатньо великої кількості числа n експериментів (див. матеріал на-

ступних лекцій).

Отже, математичне очікування випадкової величини наближено дорівнює середньому арифметичному із спостережуваних значень випадкової величини тим точніше, чим більше спо-

стережень здійснюється.

Приклад 2. Знайти математичне очікування суми Х очків, що випадають на верхній грані кожної з трьох підкинутих гральних кубиків.

▼Можливі значення випадкової величини Х належать дискретній множині

{3;4;5; 17;18}. Але немає потреби знаходити ряд розподілу величини Х – недоцільно знаходити ймовірності загалом нерівноможливих подій: Р(Х=3), Р(Х=4), Р(Х=18). Підемо значно простішим шляхом: Х=Х1+Х2+Х3, де Х1 – випадкова величина, що дорівнює числу очків на 1-му кубику, Х2 і Х3

– відповідно на 2-му і 3-му кубиках. Оскільки Х1, Х2, Х3 – незалежні випадкові величини, то

М(Х)=М(Х1)+М(Х2)+М(Х3). Закони розподілу величин Х1, Х2, Х3 однакові:

Хі; і=1,2,3	1	2	3	4	5	6
Р	1/6	1/6	1/6	1/6	1/6	1/6

Отже, М(Хі)=(1+2+3+4+5+6)/6=21/6=7/2, звідки дістанемо: М(Х)=3 (7/2)=10,5. ▲

Мода та медіана випадкової величини

Мода Мо дискретної величини Х – це таке значення із всіх її можливих значень хі, імовір-

ність якого рі найбільша.

Модою неперервного розподілу є те можливе значення Мо випадкової величини, за якого щільність розподілу f(x) має максимум.

Якщо ймовірність (для дискретної випадкової величини) або щільність ймовірності досягає максимуму не в одній, а в декількох точках, розподіл називають полімодальним. Існують також і розподіли, які не мають моди. Їх називають антимодальними.

Медіаною Ме неперервної випадкової величини Х називають те її можливе значення, для якого виконується рівність імовірностей таких подій:

P X Me P Me X
F (Me) F ( ) F ( ) F (Me)

F (Me) F (Me) F ( ) F ( ) 1

8

	F (Me)	1	.			(9)
	2
Отже, медіаною Ме випадкової величини Х є корінь рівняння F x 0,5 , де F(х) – функ-
ція розподілу ймовірностей.
Оскільки P X Me	P Me X				Me
					f (x)dx	f (x)dx , то якщо
						Me

провести пряму х=Ме на графіку щільності розподілу випадкової величини, то вона поділить пло-

щу криволінійної трапеції, яка обмежена згори функцією f(x), а знизу – віссю Оx, на дві рівновеликі

частини.

2.2. Характеристики розсіювання: дисперсія та середнє квадратичне відхилення випадко-

вої величини, їхні властивості.

Математичне очікування не дає достатньо повної інформації про випадкову величину,

оскільки може бути таке, що математичні очікування випадкових величин однакові, хоча можливі значення цих випадкових величин суттєво відрізняються і випадкові величини мають різний роз-

мах розсіювання відносно математичного очікування. Тому математичне очікування називають

центром розсіювання. Для того, щоб оцінити міру розсіювання можливих значень випадкової величини навколо її математичного очікування, використовують числову характеристику, яку на-

зивають дисперсією.

Розглянемо відхилення випадкової величини Х від її математичного очікування, тобто ви-

падкову величину Х–М(X). Обчислимо її математичне очікування: М[Х-М(Х)]=М(Х)-М(Х)=0, оскі-

льки математичне очікування випадкової величини є її числовий параметр, тобто стала величина,

тому М[М(Х)]=М(Х).

Отже, математичне очікування відхилення дорівнює нулю, оскільки від’ємні відхилення можливих значень випадкової величини від її математичного очікування в сумі компенсуються додатними, тому за міру розсіювання випадкової величини навколо її математичного очікування

розглядають не середнє значення відхилення, а математичне очікування (середнє значення) квад-

рата відхилення.

Означення 6. Дисперсією дискретної випадкової величини називають математичне очі-

кування квадрата відхилення випадкової величини від її математичного очікування:

D(X)=M[(X–M(X))2]=M(X2)–(M(X))2, (10)

оскільки M[X2–2XM(X)+(M(X))2]=M(X2)–2M(X) M(X)+(M(X))2 на підставі того, що математичне очі-

кування випадкової величини та її квадрата є постійні параметри.

Для неперервної випадкової величини Х, що набуває значень з інтервалу [ ; ] і задана щільністю (густиною) розподілу f(x), дисперсію знаходять за однією з наступних формул, які як і у

9

випадку формули (7) для математичного очікування, отримуються на основі формул (7, 10) із за-

стосуванням операції довільного поділу проміжку [ ; ] на n елементарних проміжківxi (i 1, 2,..n) , подальшого вибору в кожному з них довільно точки хі та граничного переходу у відповідній інтегральній сумі за прямування до нуля найбільшого з проміжків; при цьому добуток значення щільності розподілу на величину проміжку, f(хі) хі, приблизно рівний ймовірності попа-

дання хі в проміжок хі:

β
D( X ) (x M ( X ))2 f (x)dx 2,	(11)
α
або
β
D( X ) x2 f (x)dx (M ( X ))2 .	(12)

α

У випадку неперервної випадкової величини, заданої на всій числовій осі, проміжок

[ ; ] інтегрування в цих формулах потрібно замінити на ( ;+ ).

Слід пам’ятати, що дисперсія не може бути від’ємною величиною,

D(Х) 0.

Середнє квадратичне відхилення

Оскільки дисперсія має розмірність квадрата випадкової величини, за характеристику її ро-

зсіювання навколо математичного очікування беруть середнє квадратичне відхилення (X) –

корінь квадратний із дисперсії:

σ( X ) D( X )		(13)

Розмірність (X) співпадає з розмірністю випадкової величини X. На графіку щільності ро-

зподілу f(x) величина (X) зображається на осі ОX відстанню від М(X) в обидва боки.

Властивості дисперсії

випливають із її визначення за формулами (10) та відповідних властивостей математичного очіку-

вання.

1. Дисперсія сталої величини С дорівнює нулю:

D(С)=0.

2. Сталий множник можна виносити за знак дисперсії, попередньо піднісши його до квад-

рату:

D(CX)=С2D(X).

3. Дисперсія суми двох незалежних випадкових величин дорівнює сумі дисперсій цих вели-

чин:

D(X+Y)=D(X)+D(Y).

10

4. Дисперсія різниці двох незалежних випадкових величин дорівнює сумі дисперсій цих величин:

D(X–Y)=D(X)+D(Y).

5. Із застосуваням сполучного закону додавання, для суми скінченної кількості випадкових величин, кількість яких більша двох, на основі властивості дістанемо: дисперсія суми незалежних в сукупності випадкових величин дорівнює сумі дисперсій цих величин.

Відповідно, середнє квадратичне відхилення суми скінченної кількості взаємно незалеж-

них випадкових величин рівне:

σ( X1 X2 Xn ) 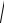σ2 ( X1) σ2 ( X2 ) ... σ2 ( Xn ) .

Нормування випадкової величини

Якщо від випадкової величини X віднімемо її математичне очікування, то дістанемо

центровану випадкову величину X0, математичне очікування якої дорівнює нулю:

X 0=Х-М(Х). (14) Справді, М(X0)=М[X-М(Х)]=М(Х)-М[М(Х)]=М(Х)-М(Х)=0.

Ділення центрованої випадкової величини на її середнє квадратичне відхилення назива-

ється нормуванням цієї випадкової величини.

Нормована випадкова величина X 0 X M ( X ) має нульове математичне очікування

σ(X )

й одиничну дисперсію.

Приклад 3. Знайти математичне очікування, дисперсію та середнє квадратичне відхилення дискретної випадкової величини X, якщо маємо її ряд розподілу:

X	0,1	2	10	20
Р	0,4	0,2	0,15	0,25

▼ Знайдемо математичне очікування випадкової величини X:

М(X)=0,1 0,4+2 0,2+10 0,15+20 0,25=0,04+0,4+1,5+5=6,94.

Знайдемо математичне очікування випадкової величини X2:

М(X2)=0,12 0,4+22 0,2+102 0,15+202 0,25=0,004+0,8+15+100=115,804.

Знайдемо дисперсію:

D(X)=M(X2)–(M(X))2=115,804–(6,94)2=67,6404.

Дисперсію ми могли знайти й за іншою формулою:

D( X ) M (( X M ( X ))2 ) (0.1 6.94)2 0.4 (2 6.94)2 0.2 (10 6.94)2 0.15 (20 6.94)2 0.25 18.71424 4.88072 1.40454 42.6409 67, 6404.

Результат той самий.