Mathcad - ЛР6

Вывод: В ходе проведенного численного эксперимента с заданными параметрами было промоделировано движение груза на пружином подвесе под воздействием силы, подчиняющейся синусоидальному закону. Во всех рассмотренных случаях колебания груза не являлись затухающими, т.к. в колебательной системе существовал источник энергии. Все вышеперечисленные три варианта отличались только лишь коэффициентом упругости пружины. Наблюдая за графиками можно сделать вывод, что чем большую упругость имеет пружина, тем сильнее отличия результирующих колебаний от вынуждающих. Стоит отметить, что частота вынуждающих колебаний была значительно выше частоты собственных колебаний системы, что не позволило проявится резонансу.

В последнем рассмотренном случае на груз подействовала сила такая, как если бы к существующему грузику подвесили бы ещё один. Пружина растянулась и подвергалась некоторое время затухающим колебаниям.

Задача 6.3. Разработать процедуры и решить приближенно задачу Коши для ОДУ 1 порядка вида (1),

используя

1.метод Эйлера первого порядка точности,

2.модифицированный метод Эйлера второго порядка точности,

3.метод Эйлера-Коши второго порядка точности,

4.неявный метод Эйлера первого порядка точности,

5.метод Рунге-Кутты 4 порядка точности (без использования встроенной функции)

с шагами h =	T − t0	и h / 2 . Для каждого метода оценить погрешность по правилу Рунге и вычислить
100

уточненное решение (см. ПРИЛОЖЕНИЕ 6.C). Для каждого метода построить на одном чертеже график приближенного решения (с шагом h / 2), график уточненного решения, график точного аналитического решения. Сделать выводы.

Теоретический материал:

Правило Рунге практической оценки погрешности (правило двойного пересчета):

Одним из наиболее простых, широко применяемых и достаточно эффективных методов оценки погрешности и уточнения полученного решения при численном решении ОДУ является правило Рунге. Для оценки погрешности решения дифференциального уравнения (разницы между точным и приближенным решением в узлах) применяют первую формулу Рунге:

		y(h / 2)					y(ti ) − yi(h / 2) ≈ εi(h) ,
где εi(h)	=			− y(h)
			2i		i		, i= 0, … , n – задает номера узлов сетки ti , построенной с шагом h , p – порядок
			2 p	−1
метода,	yi(h)		и y2(hi		/ 2)	- приближенные решения уравнения с шагом h и h / 2 соответственно в узле ti .

Уточненное решение вычисляется по формуле:

yi, уточн = y2(hi / 2) + εi(h) , i=0,…, n.

Явный метод Эйлера 1-го порядка:

yi+1 = yi + hf (xi , yi )

Неявный метод Эйлера 1-го порядка:

yi+1 = yi + hf (xi+1, yi+1 )

Усовершенствованный метод Эйлера 2-го порядка yi+1 = yi + hf (xi + 0.5h, yi + 0.5hf (xi , yi ))

Метод Эйлера-Коши 2-го порядка (схема «предиктор-корректор»):

y

= y + hf (t , y ),

y

= y + h

( f (t , y ) + f (t

, y

+1

))

i+1

i

i

i

i+1

i

2

i

i

i+1

i

Метод Рунге-Кутты 4-го порядка:

yi+1

= yi + h (ki(1)

+ 2ki(2)

+ 2ki(3) + ki(4) )

6

ki(1) = f (xi , yi ) , ki(2)

= f (xi + 0.5h, yi

+ 0.5hki(1) )

k (3)

= f (x

i

+ 0.5h, y

i

+ 0.5hk (2) ) ,

k(4) = f (x + h, y

i

+ h×k

(3) )

i

i

i

i

i

Исходные данные:

Правая часть уравнения:

f(t , y) := -t×y - t3

Начальное значение:

Число узлов сетки:

Решение задачи:

y0 := 3	Отрезок:	t0 := 0	T := 1
N := 100	i := 0 .. N

Шаг сетки: h :=	T - t0			h = 0.01	x := t0 + i×h
	N				i
	−	t2
yTrue(t) := 2 - t2 + e 2				- точное значение функции

1) Расчет методом Эйлера первого порядка точности:

eyler(f , y0, t0 , h, N) := y0 ¬ y0

for i Î 0 .. N - 1

yi+1 ¬ yi + h×f(t0 + i×h, yi)

y

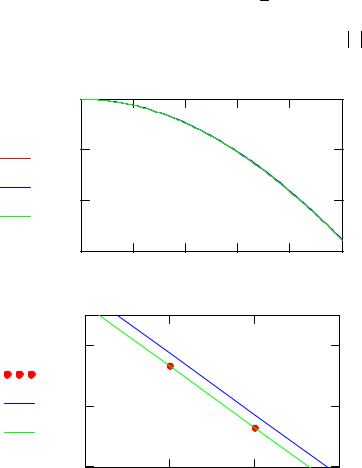
yE := eyler(f , y , t0 , h, N)		yE2 := eyleræf , y			, t0 , h	, 2Nö
0			è	0	2	ø
Ei := yE22×i - yEi		yE_Ci := yE22×i + Ei				mE := max(	E )	mE = 0.03319307271477
	3
yTrue(xi)	2.5
yE22×i
yE_Ci	2
	1.5 0	0.2	0.4		0.6	0.8
			xi
yTrue(xi) 2.24
yE22×i
yE_Ci	2.22
	2.20.72		0.73		0.74
			xi
2) Расчет усовершенствованным методом Эйлера второго порядка точности:

eylerEnh(f , y0 , t0 , h, N) :=		y0 ¬ y0
		for i Î 0 .. N - 1
		yi+1 ¬ yi + h×f(t0 + i×h + 0.5		×h, yi	+ 0.5×h×f(t0 + i×h , yi))
		y
yEEnh := eylerEnh(f , y , t0 , h, N)			yEEnh2 := eylerEnh	æf , y	, t0 ,	h	, 2Nö
0				è 0	2			ø
Ei := yEEnh22×i - yEEnhi	yEEnh_Ci		:= yEEnh22×i + Ei mEEnh := max(						E		)

mEEnh = 5.92028716900001 ´ 10- 5

	3
yTrue(xi)	2.5
yEEnh22×i
yEEnh_Ci 2
	1.5	0	0.2	0.4	0.6	0.8
					xi
yTrue(xi) 2.24
yEEnh22×i
yEEnh_Ci	2.22

2.2	0.73	0.74
0.72

xi

3) Расчет методом Эйлера-Коши 2-го порядка точности (схема "предиктор-корректор"):

eylerKoshy(f , y0, t0 , h, N) :=	y0 ¬ y0
	t10 ¬ 1
	for	i Î 0 .. N - 1
	yi+1 ¬ yi +		h		×éf(t0 + i×h, yi) + fét0 + (i + 1) ×h, yi + h×f(t0 + i×h, yi)ùù
		2			ë	ë			ûû
	y
yEK := eylerKoshy(f , y , t0 , h, N)		yEK2 :=			eylerKoshyæf , y	, t0 ,	h		, 2Nö
							2
0					è 0				ø
Ei := yEK22×i - yEKi	yEK_Ci := yEK22×i + Ei

	3					mEK := max(	E )
yTrue(xi)	2.5
						mEK = 6.63667365979669 ´ 10- 5
yEK22×i
yEK_Ci	2
	1.5	0	0.2	0.4	0.6	0.8
					xi
yTrue(xi) 2.24
yEK22×i
yEK_Ci	2.22
	2.20.72			0.73	0.74
					xi
4) Расчет неявным методом Эйлера первого порядка точности:

ImplicitEyler(f , y0 , t0 , h , N) :=

y0 ¬ y0

ys ¬ 1015

for

i Î 0 .. N - 1

yi+1 ¬ yi + h×f(t0 + i×h, yi)

> 10- 15

while

yi+1 - ys

ys ¬ yi+1

yi+1

¬ yi +

h

×éf(t0 + i×h, yi) + f[t0 + (i + 1) ×h , ys]ù

2

ë

û

y

yIE := ImplicitEyler(f , y

, t0 , h, N)

yIE2 :=

ImplicitEyleræf , y , t0 ,

h

, 2Nö

2

0

è

0

ø

Ei := yIE22×i - yIEi

yIE_Ci := yIE22×i + Ei

	3
yTrue(xi)	2.5
yIE22×i
yIE_Ci	2
	1.5 0	0.2	0.4	0.6	0.8
				xi

mIE := max( E )

mIE = 2.66292374223529 ´ 10- 5

yTrue(xi) 2.24

yIE22×i

2.22

yIE_Ci

2.20.72
	0.73		0.74
			xi

5) Расчет методом Рунге-Кутты 4-го порядка точности:

RungeKutt(f , y0, t0 , h , N) :=

y0 ¬ y0

for

i Î 0 .. N - 1

k1i ¬ f(t0 + i×h , yi)

k2i ¬ f(t0 + i×h + 0.5 ×h, yi

+ 0.5×h×k1i)

k3i ¬ f(t0 + i×h + 0.5 ×h, yi

+ 0.5×h×k2i)

k4i ¬ f(t0 + i×h + h, yi + k3i ×h)

y

¬ y +

h

×(k1

i

+ 2×k2

i

+ 2×k3

i

+ k4 )

i+1

i

6

i

y

yRK := RungeKutt(f , y , t0 , h, N)

yRK2 :=

RungeKuttæf , y , t0 ,

h

, 2Nö

0

è

0

2

ø

Ei := yRK22×i - yRKi

yRK_Ci := yRK22×i

+ Ei

mRK := max(

E

)

	3					mRK = 4.93886169201403 × 10− 10
yTrue(xi)
	2.5
yRK22×i
yRK_Ci	2
	1.5	0	0.2	0.4	0.6	0.8
					xi

yTrue(xi) 2.24

yRK22×i

2.22

yRK_Ci

2.20.72
	0.73		0.74
			xi

Произведем сравнение использованных методов по максимальной погрешности результата: 1) Метод Эйлера первого порядка точности:

mE = 0.03319307271477

2) Усовершенствованный метод Эйлера второго порядка точности:

mEEnh = 5.92028716900001 × 10− 5

3) Метод Эйлера-Коши 2-го порядка точности (схема "предиктор-корректор"):

mEK = 6.63667365979669 × 10− 5

4) Неявный метод Эйлера первого порядка точности:

mIE = 2.66292374223529 × 10− 5

5) Метод Рунге-Кутты 4-го порядка точности:

mRK = 4.93886169201403 × 10− 10

Вывод: В ходе проведенного численного эксперимента метод Рунге-Кутты четвертого порядка точности показал наилучший результат по точности. Наихудший результат был у метода Эйлера. Неявный метод Эйлера первого порядка позволил достичь точности, даже превосходящей точность метода более высокого порядка, метода Эйлера-Коши. Это объясняется тем, что в текущей

реализации неявного метода Эйлера применялось большое количество итераций минимизации погрешности на каждом шаге, что позволило значительно улучшить результат, но потребовало большее количество процессорного времени, по сравнению с методом Эйлера-Коши. Усовершенствованный метод Эйлера второго порядка приблизительно соответствовал методу Эйлера-Коши, что объясняется равенством их порядков точности.

Задача 6.4. Решить приближенно задачу Коши для ОДУ 3 порядка

a0 y′′′ + a1y′′ + a2 y′ + a3 y = f (t) y(A) = b1, y′(A) = b2 , y′′(A) = b3

на отрезке [A,B] с помощью встроенной функции rkfixed пакета MATHCAD с шагами h=0.1 и h=0.05 для систем ОДУ 1 порядка. Оценить погрешность по правилу Рунге. Построить график решения, найденного с шагом h=0.05.

Теоретический материал:

Сведение ОДУ 3 порядка к системе ОДУ 1 порядка:

y1′ = y2 y2′ = y3

y3′ = f (t) − a1y3 − a2 y2 − a3y1 a0

y1(A) = b1, y2( A) = b2 , y3( A) = b3 .

Исходные данные:

Функция правой части:

Отрезок:

f(t) := sin(2t) + 2×t - 1

A := 0 B := 2

a0 := 1 a1 := 1.4 a2 := 1.88 a3 := 18 y1 := 1.5 y2 := 2.9 y3 := 2

Шаг сетки: h := 0.1

Решение задачи:

i := 0 .. N		ti	:= t0 + i×h	Число узлов сетки:						N := B - A
										h
Формирование вектора правой части системы ОДУ (1) и вектора начальных
условий для применения встроенной функции rkfixed:
f1(t , y1, y2, y3) := y2
f2(t , y1, y2, y3) := y3
f3(t , y1, y2, y3) := f(t) - a1×y3 - a2×y2 - a3×y1
				a0
æy1 ö			æf1(t , y0 , y1 , y2) ö
y := çy2 ÷			D (t , y) := ççf2(t , y0 , y1 , y2) ÷÷						RK4_h := rkfixed(y, A , B , N , D)
ç	÷		ç	f3(t , y , y , y			)	÷
èy3	ø		è					ø
				0	1	2
График решения с шагом h=0.1
			5
			0		1				2
		RK4_hi , 1
			5
			10
					RK4_hi , 0
Шаг сетки:			h := 0.05	Число узлов сетки:						N := B - A	RK4_h_2 := rkfixed(y, A , B , N , D)
i := 0 .. N										h
График решения с шагом h=0.05
			5
			0		1				2
		RK4_h_2i , 1
			5
			10
				RK4_h_2i , 0
h := 0.1		N := B - A		i := 0 .. N
			h

Вычисление погрешности по правилу Рунге:

ERK4i :=	RK4_h_22×i, 1	− RK4_hi, 1	max(ERK4)	= 6.9292724536633 × 10- 6
	15

Вывод: В ходе проведенного численного эксперимента ОДУ 3-го порядка было решено через сведение к системе ОДУ 1-го порядка. Абсолютная погрешность,

вычисленная по правилу Рунге, составила 6.9292724536633 × 10- 6.

Задача 6.5. Задано линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами и

начальные условия:

y¢¢ + p × y¢ + q × y = f (t)

y(a) = b1 , y¢(a) = b2

Сведя уравнение к системе ОДУ 1-го порядка, найти численное решение задачи на отрезке t Î[A, B]

методом Эйлера-Коши с заданной точностью ε = 10−3 . ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

1.Свести уравнение к системе ОДУ 1-го порядка вида:

ìy¢ =

ïïz¢ =

í

ïy(a)

ïîz(a)

z

f (t) - p × z - q × y

=b1

=b2

2.Найти решение системы (см. ПРИЛОЖЕНИЕ 6.C) методом Эйлера-Коши c начальным шагом

h = B10- A .

3.Постепенно уменьшая шаг вдвое и оценивая каждый раз достигнутую погрешность по правилу Рунге, найти решение задачи с заданной точностью ε.

4.Вывести на один чертеж график полученного приближенного решения и график точного аналитического решения. Сравнивая приближенное и точное решение, оценить фактически достигнутую практическую погрешность.

5.Объяснить полученные результаты. Сделать выводы.

Теоретический материал:

ìy¢ = f (t, y, z) ïïz¢ = g(t, y, z)

íïy(t0 ) = y0 ïîz(t0 ) = z0

ti = t0 + h ×i h (yi , zi )

ìïyi+1 = yi + hf (ti , yi , zi ) ïzi+1 = yi + hg(ti , yi , zi )