
- •Контрольні питання:
- •Контрольні питання: Теоретичні відомості
- •Завдання:
- •Теоретичні відомості
- •Різні види рівнянь прямої лінії
- •Варіант № 1
- •Практична робота №7
- •Контрольні питання
- •Теоретичні відомості
- •Варіант 1
- •Завдання для самостійного виконання
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •3. Вычисление площадей плоских фигур
- •Задания для самостоятельного решения
- •4. Вычисление объёмов тел вращения
- •Задания для самостоятельной работы
- •5. Решение некоторых физических задач с помощью определённого интеграла
- •Задания для самостоятельного решения
- •Вопросы для самопроверки
Практична робота №1
Тема: Обчислення визначників. Дії з матрицями.
Мета: Навчитися обчислювати визначники різними способами, виконувати дії з матрицями.
Приклади виконання типових завдань:
Приклад
1:
Знайти суму і різницю матриць:
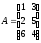 ;
;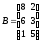 .
.
 ;
;
 .
.
Приклад 2: Дано матриці А та В. Знайти добуток АВ. Число стовпців матриці А дорівнює числу строк матриці В, тому добуток АВ можливий.
 ;
;
 .
.

 .
.
Приклад 3: Обчислення визначника:
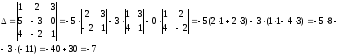
Завдання
Варіант 1
Обчислити самостійно визначник всіма відомими способами:
а) за визначенням;
б) перетвореннями.
1)
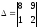 ;
2)
;
2)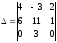 ;
3)
;
3) ; 4 )
; 4 )
 .
.
дії з матрицями:
а)
Дано матриці:
 ;
; .
.
Знайти: 1) А-В; 2) А+В; 3) 3А-В; 4) В+2А.
б)
Знайти добуток АВ матриць:
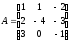 ;
;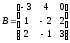 .
.
в)
Дано
матриці:
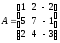 ;
;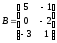 .Знайти
добуток BA.
.Знайти
добуток BA.
Варіант 2
Обчислити самостійно визначник всіма відомими способами:
а) за визначенням;
б) перетвореннями.
1)
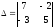 ;
2)
;
2)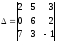 ; 3)
; 3)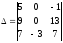 ;
4)
;
4)
дії з матрицями:
а)
Дано матриці:
 ;
; .
.
Знайти: 1) А-В; 2) А+В; 3) 3А-В; 4) В+2А.
б)
Дано
матриці:
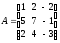 ;
; .Знайти
добуток АВ.
.Знайти
добуток АВ.
в)
Знайти добутки матриць АВ та ВА:
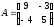 ;
;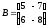 .
.
Варіант 3
Обчислити самостійно визначник всіма відомими способами:
а) за визначенням;
б) перетвореннями.
1)
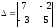 ;
2)
;
2)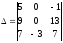 ;
3)
;
3)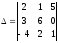 ;
4 )
;
4 )

дії з матрицями:
а)
Дано матриці:
 ;
; .
.
Знайти: 1) А-В; 2) А+В; 3) 3А-В; 4) В+2А.
б)
Дано
матриці:
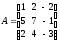 ;
;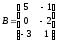 .Знайти
добуток BA.
.Знайти
добуток BA.
в)
Знайти добутки АВ та ВА матриць:
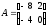 ;
;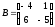 .
.
Варіант 4
Обчислити самостійно визначник всіма відомими способами:
а) за визначенням;
б) перетвореннями.
1)
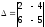 ;
2)
;
2)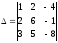 ;
3)
;
3) ;
4)
;
4)
дії з матрицями:
а)Дано
матриці:
 ;
; .
.
Знайти: 1) B-A; 2) А+2В; 3) 4А-В; 4) 3В+2А.
б)
Дано
матриці:
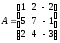 ;
;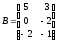 .Знайти
добуток АВ.
.Знайти
добуток АВ.
в)
Знайти добутки АВ та ВА матриць:
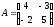 ;
; .
.
Варіант 5
Обчислити самостійно визначник всіма відомими способами:
а) за визначенням;
б) перетвореннями.
1)
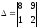 ;
2)
;
2)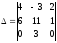 ;
3)
;
3) ;
4)
;
4)
дії з матрицями:
а)
Дано матриці:
 ;
; .
.
Знайти: 1) А-В; 2) B+A; 3) А+4В; 4) 2В-3А.
б)
Дано
матриці:
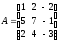 ;
;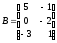 .Знайти
добуток BA.
.Знайти
добуток BA.
в)
Знайти добутки матриць АВ та ВА:
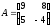 ;
;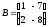 .
.
Варіант 6
Обчислити самостійно визначник всіма відомими способами:
а) за визначенням;
б) перетвореннями.
1)
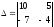 ;
2)
;
2)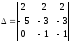 ;
3)
;
3)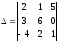 ;
4)
;
4) .
.
дії з матрицями:
а)
Дано матриці:
 ;
; .
.
Знайти: 1) А-В; 2) 2А+В; 3) 5А+2В; 4) В-3А.
б)
Знайти добуток матриць ВА:
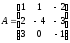 ;
;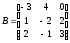 .
.
в)
Знайти добуток матриць АВ:
 ;
; .
.
Практична робота №2
Тема: Розв’язування систем лінійних рівнянь методом Гаусса, за правилом Крамера.
Мета: Узагальнення і систематизація знань з теми «Розв’язування систем лінійних рівнянь»
Завдання: Виконати завдання згідно вашому варіанту. Оформити роботу. Відповісти на контрольні запитання.
Зміст звіту: 1. Тема роботи. 2. Мета роботи. 3. Завдання до роботи. 4. Порядок виконання завдань. 5. Підсумки виконання роботи.
Контрольні питання:
Метод Гауса.
Розв’язок систем рівнянь за правилом Крамера.
Матричний метод розв’язку систем лінійних рівнянь
Розв’язок систем рівнянь за допомогою оберненої матриці.
ХІД РОБОТИ:
Типові приклади
1. Розв’язати систему лінійних рівнянь методом Крамера
У
випадку коли
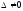
 система
має єдиний розв’язок, який знаходиться
за формулами Крамера:
система
має єдиний розв’язок, який знаходиться
за формулами Крамера: .
.
Розв’яжемо
систему
 .
.
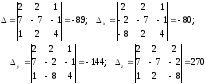
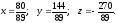
2. Розв’язати систему лінійних рівнянь методом Гауса.
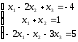

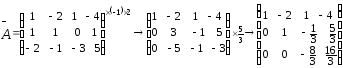 .
.
Система рівнянь
має вигляд
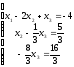 .
Із третього рівняння
.
Із третього рівняння
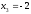 ,
дане значення підставимо у попереднє
рівняння
,
дане значення підставимо у попереднє
рівняння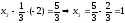 .
.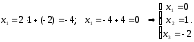
Варіант 1.
1. Розв’язати системи лінійних рівнянь за правилом Крамера і методом Гауса.
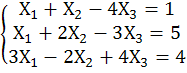
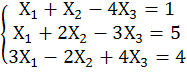 Б)
Б) 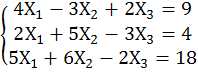

2. Розв’язати систему лінійних рівнянь за допомогою оберненої матриці.
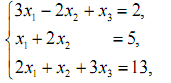
Варіант 2
1. Розв’язати системи лінійних рівнянь за правилом Крамера і методом Гауса.

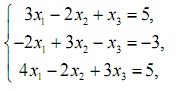
2. Розв’язати систему лінійних рівнянь за допомогою оберненої матриці.
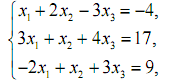
Варіант 3
1. Розв’язати системи лінійних рівнянь за правилом Крамера і методом Гауса.
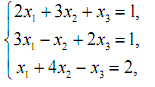
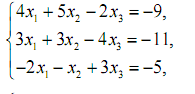
2. Розв’язати систему лінійних рівнянь за допомогою оберненої матриці.

Варіант 4
1. Розв’язати системи лінійних рівнянь за правилом Крамера і методом Гауса.
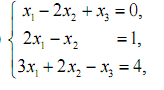
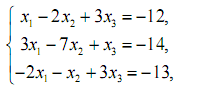
2. Розв’язати систему лінійних рівнянь за допомогою оберненої матриці.
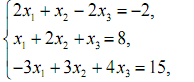
Варіант 5
1. Розв’язати системи лінійних рівнянь за правилом Крамера і методом Гауса.
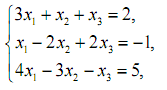
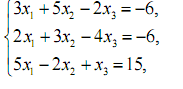
2. Розв’язати систему лінійних рівнянь за допомогою оберненої матриці.
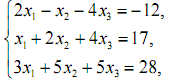
Варіант 6
1. Розв’язати системи лінійних рівнянь за правилом Крамера і методом Гауса.

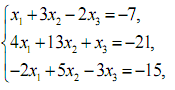
2. Розв’язати систему лінійних рівнянь за допомогою оберненої матриці.

Варіант 7
1. Розв’язати системи лінійних рівнянь за правилом Крамера і методом Гауса.
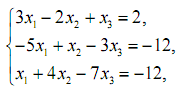
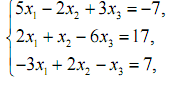
2. Розв’язати систему лінійних рівнянь за допомогою оберненої матриці.
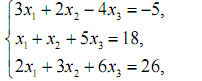
Варіант 8
1. Розв’язати системи лінійних рівнянь за правилом Крамера і методом Гауса.
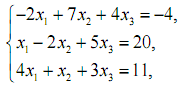

2. Розв’язати систему лінійних рівнянь за допомогою оберненої матриці.
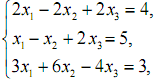
Варіант 9
1. Розв’язати системи лінійних рівнянь за правилом Крамера і методом Гауса.
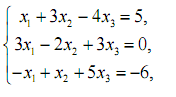
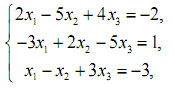
2. Розв’язати систему лінійних рівнянь за допомогою оберненої матриці.
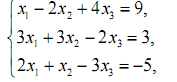
Варіант 10
1. Розв’язати системи лінійних рівнянь за правилом Крамера і методом Гауса.
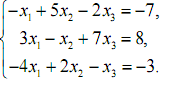
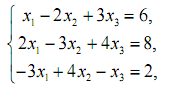
2. Розв’язати систему лінійних рівнянь за допомогою оберненої матриці.

Практична робота №3
Тема: Дії над векторами заданими власними координатами.
Мета: Повторити поняття вектора на площині та в просторі, поняття колінеарності і компланарності векторів, відпрацювати дії з векторами, познайомитись з векторним і мішаним добутками та їх використанням в геометрії.
Завдання: Виконати завдання згідно вашому варіанту. Оформити роботу. Відповісти на контрольні запитання.
Зміст звіту: 1. Тема роботи. 2. Мета роботи. 3. Завдання до роботи. 4. Порядок виконання завдань. 5. Підсумки виконання роботи.
Контрольні питання: Теоретичні відомості
Векторний і мішаний добутки векторів та їх властивості
Упорядкована
трійка некомпланарних векторів
 ,
,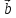 ,
,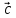 із загальним початком в точці О
називається правої, якщо найкоротший
поворот від вектора
із загальним початком в точці О
називається правої, якщо найкоротший
поворот від вектора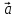 до вектора
до вектора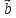 спостерігається
з кінця вектора з тим, що відбувається
проти руху годинникової стрілки. В
іншому випадку дана трійка називається
лівою.
спостерігається
з кінця вектора з тим, що відбувається
проти руху годинникової стрілки. В
іншому випадку дана трійка називається
лівою.

Векторним
добутком векторів
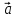 і
і називається
вектор
називається
вектор
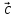 ,
що позначається
,
що позначається
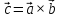 ,
або (
,
або (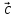 =
=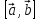 ,
який
задовольняє наступним трьом умовам:
,
який
задовольняє наступним трьом умовам:
1.
|
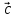 |
= |
|
= |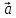 | |
| | | sin (
| sin (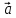 ^
^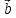 );
);
2.
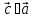 ,
,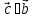 ;
;
3.
трійка
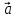
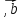 ,
,
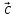 –
права.
–
права.
Основні властивості векторного добутку векторів:
1. ;
;
2.
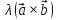 =
=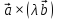 ;
;
3.
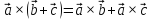 ;
;
4.
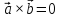 ,
якщо
,
якщо
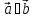 ;
;
5.
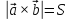 ,
де
,
де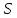 – площа
паралелограма, побудованого на векторах
– площа
паралелограма, побудованого на векторах
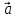 та
та
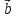 ,
що мають спільний початок у точці φ.
,
що мають спільний початок у точці φ.
Якщо
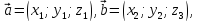 то векторний добуток виражається через
координати даних векторів
то векторний добуток виражається через
координати даних векторів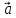 і
і
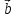 ,
таким чином:
,
таким чином:
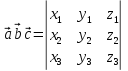
Приклад
1.
Дано вектори
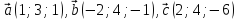 .
Потрібно встановити, чи компланарні
дані вектори, у разі їх некомпланарності
з'ясувати, яку трійку (праву або ліву)
вони утворюють, і обчислити об’єм
побудованого на них паралелепіпеда.
.
Потрібно встановити, чи компланарні
дані вектори, у разі їх некомпланарності
з'ясувати, яку трійку (праву або ліву)
вони утворюють, і обчислити об’єм
побудованого на них паралелепіпеда.
Розв’язання: Обчислимо:

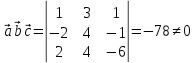
із
значення мішаного добутку випливає, що
вектори не компланарні і утворюють
ліву трійку, об’єм паралелепіпеда
побудованого на даних векторах
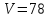 .
Відповідь:
.
Відповідь: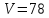 .
.
Приклад
2.
Обчислити площу паралелограма,
побудованого на
векторах
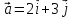 ,
,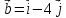 . Тут
. Тут
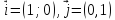 –
одиничні
вектори, взаємно перпендикулярні.
–
одиничні
вектори, взаємно перпендикулярні.
Розв’язання:
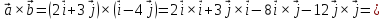
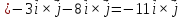 =
=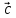 ,
,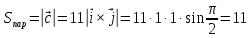 .
.
Відповідь:
 .
.
Приклад
3.
Показати, що вектори
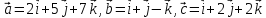 компланарні.
компланарні.
Розв’язання:
Якщо
вектори
 ,
,
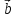 ,
,
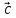 компланарні, то
компланарні, то
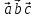 = 0.
= 0.
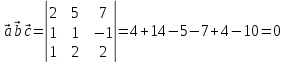
Мішаний
добуток векторів
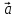 ,
,
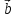 ,
,
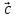 дорівнює 0, тому вектори
дорівнює 0, тому вектори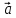 ,
,
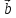 ,
,
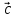 компланарні.
компланарні.
