dI		0	LI 2
	dA = dQ = dW = εci dq = −L		Idt = −LIdI	A =W = −∫LIdI =
		dt			2
			,	I

	W =	LI 2
		2 - энергия магнитного поля соленоида, определяется параметрами конкретной катушки и током, протекающим в
	ней.

Получим связь между энергией магнитного поля и его характеристиками. Пусть соленоид достаточно длинный, чтобы магнитное поле в нем можно было считать однородным, а индуктивность можно было рассчитывать по формуле

L = µ0µn2V

B = µ0 µnI . Подставив в формулу, получим :

Введем объемную плотность энергии магнитного поля:

ω

=

B2

=

µ

µH 2

=

BH

=

Br

H

M

0

2µ0 µ

2

2

2 .

W = B2 V

2µ0 µ .

Эта формула позволяет рассчитать энергию магнитного поля любой конфигурации:			dW = ωdV
W = ∫∫∫	B(x, y, z) H (x, y, z)	dV
2

ТЕМА IX. ЦЕПИ ПЕРЕМЕННОГО ТОКА.

§ 49. КОЛЕБАТЕЛЬНЫЙ КОНТУР. СВОБОДНЫЕ ЭЛЕТРОМАГНИТНЫЕ КОЛЕБАНИЯ В ИДЕЛЬНОМ КОНТУРЕ.

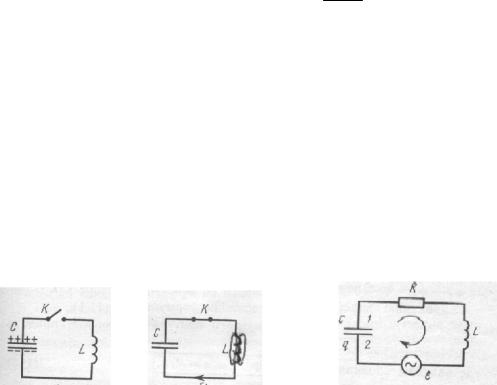
В цепи, содержащей конденсатор и катушку индуктивности , могут возникнуть электромагнитные колебания. Поэтому такая цепь называется колебательным контуром.

РИС.122 РИС.123 РИС.124

Если заряженный конденсатор замкнуть на катушку индуктивности, то в контуре возникает убывающий по величине ток (рис.122). Вследствие этого в катушке возникает ЭДС индукции, противодействующая убыванию тока, поддерживающая ток и после окончательной разрядки конденсатора. Следовательно, энергия электрического поля в конденсаторе переходит в энергию магнитного поля в катушке.

Когда конденсатор полностью разрядится, то ток в цепи поддерживается за счет энергии магнитного поля (рис.123), что приводит к перезарядке конденсатора и, соответственно, к переходу энергии магнитного поля в энергию электрического поля.

В реальном колебательном контуре необходимо учитывать сопротивление входящих в него проводников, а, следовательно, при протекании тока часть энергии электрического и магнитного поля выделяется в виде количества теплоты. Поэтому в реальном колебательном контуре электромагнитные колебания очень быстро прекращаются, а сопротивление, на котором энергия электрического тока переходит в тепловую, называется активным.

Рассмотрим колебательный контур, содержащий последовательно включенные емкость, индуктивность, активное

сопротивление и источник внешней переменной ЭДС (рис.124).

За счет

работы сторонних

сил

внешней

ЭДС совершается работа на

всех участках цепи, а следовательно:

ε(t) = −εci + IR +Uc

I = dq

εci = −L

dI

Uc

=

q

ε(t) = L dI

+ RI +

q

,

dt ,

C

или

dt

C ,

dt

53

	L	d 2q		+ R	dq	+	1	q = ε(t)
		dt	2		dt		C
								- уравнение колебаний величины заряда на пластинах конденсатора (уравнение

колебательного контура).

Его решение позволяет найти зависимость величины заряда на пластинах конденсатора от времени q=f(t), а затем I=f(t) и Uc=f(t).

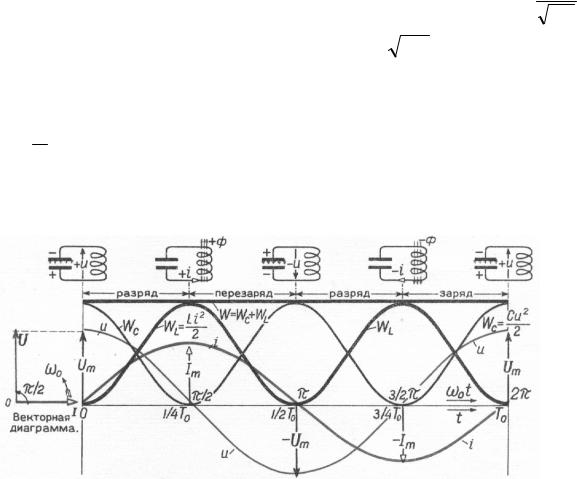
Электромагнитные колебания называются свободными, если источник внешней ЭДС отсутствует ε = 0 . Рассмотрим идеальный колебательный контур, т.е. активное сопротивление которого R=0. Пусть в начальный момент времени конденсатор полностью заряжен (рис.122).

	&&		1
			LC q = 0
В этом случае уравнение свободных колебаний:	q +				,
решением которого является q = qm cos(ω0t +ϕ0 )= qm cosω0t , т.к. при t=0 заряд конденсатора максимален.
					ω	0	=	1
Следовательно, свободные электромагнитные колебания в контуре являются гармоническими.								LC - собственная
циклическая частота электромагнитных колебаний в контуре,			T = 2π		LC - формула Томсона для периода.

Тогда

u = Cq

&		ω0t +	π
i = q = −ω0qm sinω0t = Im cos			2
				,	напряжение	на	конденсаторе

= qm cosω t =U		m	cosω t
C	0		0
			. Из этих уравнений следует, что ток опережает по фазе колебания заряда и

π

напряжения на 2 , т.е. когда ток достигает максимальной величины заряд и напряжение на конденсаторе равны нулю и наоборот (рис.125).

РИС.125

Так

как

при

R=0

потерь

энергии

на тепло

нет, то

выполняется

закон сохранения энергии:

q2

q2

Li

2

LI 2

= const

m

=

+

=

m

2C

2C

2

2

.

Следовательно,

колебания

заряда, тока

и напряжения происходят с

постоянной амплитудой, т.е. свободные колебания в идеальном контуре являются незатухающими.

Энергия электрического поля в конденсаторе и магнитного поля в катушке индуктивности, оставаясь все время положительными, также меняются по величине, но с периодом в 2 раза меньшим, чем период колебаний величины заряда и тока (рис.125).

§ 50 СВОБОДНЫЕ КОЛЕБАНИЯ В КОНТУРЕ С АКТИВНЫМ СОПРОТИВЛЕНИЕМ.

Реальный контур обладает активным сопротивлением и энергия колебаний переходит в тепловую.

54

&&

&

2

ω2

=

1

0

Уравнение свободных колебаний контура с активным сопротивлением:

q + 2βq +ω0 q = 0 , где

LC ,

2β =

R

L .

cos(ωt +ϕ)

Можно показать, что при

β 2

< ω2

q = q

e−βt

, где

qm и

0 решением этого уравнения является:

m

ϕ - произвольные постоянные, определяемые начальными условиями.

ω =

ω

2

− β

2

=

1

−

R2

0

LC

4L2

. В этом

T =

2π

=

2π

=

T0

ω

ω02 − β2

1−

β2

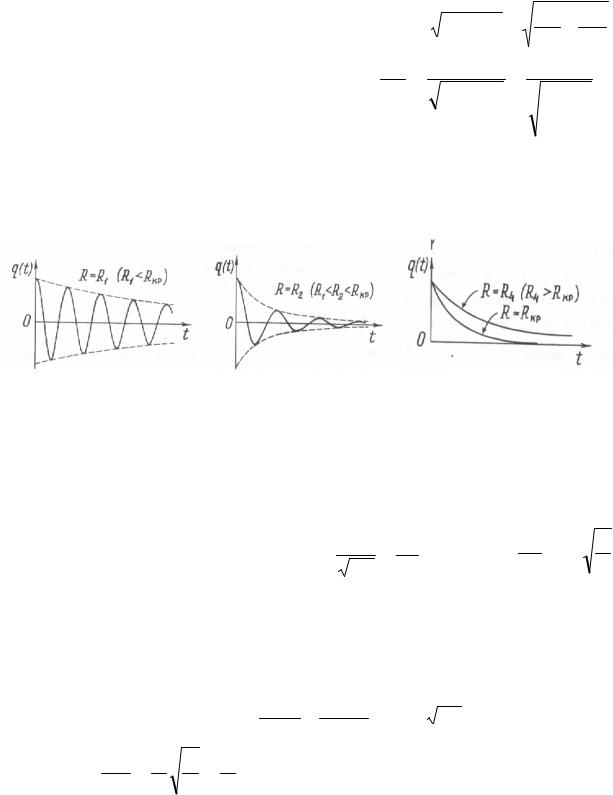
случае колебания не периодические (рис.126), но величину

ω2

0 называют

периодом затухающих колебаний, где Т0 – период свободных незатухающих колебаний.

1

Множитель qm e−βt называют амплитудой затухающих колебаний,

β =

а

β - коэффициентом затухания.

τ , где

τ - время релаксации, т.е. время, за которое амплитуда колебаний уменьшается в е раз.

РИС.126 РИС.127 РИС.128

Чем больше активное сопротивление контура, тем быстрее затухают электромагнитные колебания (рис.127).

Для характеристики скорости уменьшения амплитуды вводят логарифмический декремент затухания, равный

натуральному

логарифму

отношения

двух

значений

амплитуд,

взятых

через

период

колебания:

λ = ln

A(t)

= βT =

1

A(t +T )

Ne , где

Ne – число колебаний за время релаксации, т.е. за время, в течение которого,

амплитуда колебаний уменьшается в е раз.

A(t) – амплитудное значение соответствующей величины - qm, Um, Im.

Если затухание мало, т.е. β 2 << ω02	ω ≈ ω		=	1	=	2π	λ ≈ β	2π = πR	C
	, то	0		LC		T . Тогда		ω0	L . Для

	D = 2π	W
		δW , где W – энергия
	характеристики потери энергии в контуре за период вводится добротность контура:
	запасенная в контуре, δW - потери энергии в контуре за период.

Пусть в начальный момент заряд конденсатора равен нулю, а сила тока в контуре максимальна, следовательно, энергия контура

	W =	LIm2		δW =	Im2 RT	=	Im2 R2π	= Im2 Rπ LC
		2 . Убыль энергии за период
					2		2ω	.

D = 2π	W	=	1 L	=	π	=πNe
Тогда	δW		R C		λ	.

55

При	β 2	≥ ω2	(рис.128). Активное
		0 вместо колебаний будет происходить апериодический разряд конденсатора
		Rkp	= 2	L
сопротивление контура, при котором наступает апериодический процесс, называется критическим :				C .

§51. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С РАЗЛИЧНОЙ НАГРУЗКОЙ.

Вреальных цепях могут протекать нестационарные токи различного характера, но наиболее широко используется ток, зависящий от времени по гармоническому закону.

Реальные приборы, устройства и элементы электрических цепей, объединяемые общим термином «нагрузка», могут обладать как свойствами активного сопротивления, так и емкостными и индуктивными свойствами.

Рассмотрим, как связаны между собой ток и напряжение при различном характере нагрузки, включенной на некотором участке электрической цепи.

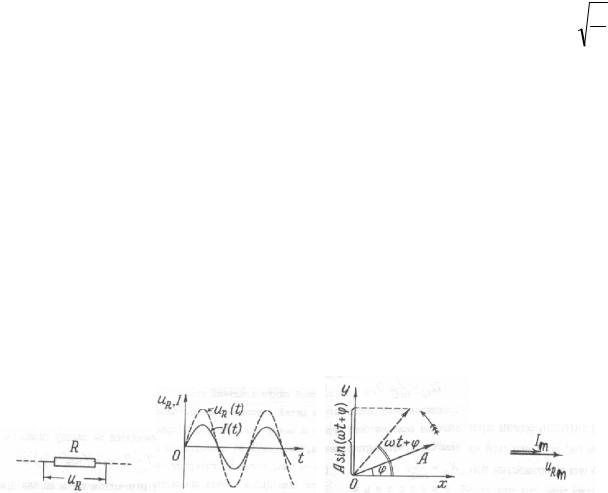
АКТИВНАЯ НАГРУЗКА (резистор).

Пусть на участке цепи с активным сопротивлением R и пренебрежимо малыми емкостью и индуктивностью (рис.129) течет

квазистационарный переменный ток i = Im sin ωt . В этом случае можем применить закон Ома для мгновенных

значений тока и напряжения: uR = iR = Im Rsinωt =URm sinωt .

Следовательно, напряжение на резисторе также совершает гармонические колебания с теми же фазой и частотой, что и

Im	=	Um
		R .
сила тока, а амплитудные значения силы тока и напряжения связаны законом Ома:				Графики зависимости
силы тока и напряжения от времени представлены на рис.130.

РИС.129 РИС.130 РИС.131 РИС.132

Для более наглядного представления используем метод векторных диаграмм. Согласно этому методу, каждой гармонически изменяющейся со временем величине: y = Asin(ωt +ϕ) можно сопоставить вектор длиной А,

который равномерно вращается в плоскости XOY с угловой скоростью ω и начальной фазой ϕ . Мгновенное значение гармонической величины, в этом случае, представляет собой проекцию вектора А на ось OY (рис.131).

Для резистора в рассмотренном случае соответствующие вектора для представления силы тока и напряжения на векторной диаграмме совпадают (рис.132).

ЕМКОСТНАЯ НАГРУЗКА

Рассмотрим участок цепи с конденсатором емкостью С, активное сопротивление которого и индуктивность

пренебрежимо малы (рис.133). Пусть на участке течет ток i = Im sin ωt .

Чтобы рассчитать напряжение на конденсаторе, найдем функциональную зависимость заряда на пластинах конденсатора

	i = dq	q =	∫	idt =	∫	Im sinωt dt = −	Im	cosωt =	Im	sin(ωt −	π )
от времени:
	dt ,						ω		ω		2

Постоянную интегрирования примем равной нулю, так как нас интересует лишь заряд конденсатора, обусловленный переменным током.

		Тогда напряжение на конденсаторе изменяется по закону:
	uc	=	q	=	Im	sin(ωt −π ) =Ucm sin(ωt −π )
			C		ωC
						2	2	, т.е. напряжение совершает колебания с той же частотой, что и
						π
	сила тока,			но отстает по фазе от силы тока на 2			(по времени – на четверть периода).

56

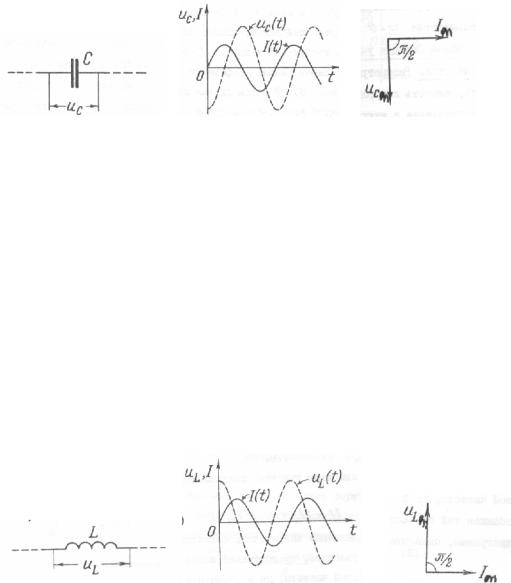
Амплитудные значения силы тока и напряжения связаны постоянным, при данных условиях, коэффициентом

	X	c	=	1
				ωC , который, при сравнении с законом Ома для резистора,		играет роль сопротивления и поэтому называется
	емкостным сопротивлением.
			Следовательно, при чисто емкостной нагрузке закон Ома для			мгновенных значений тока			и напряжения НЕ
						Im	=	Ucm		=UcmωC
								X c
	ВЫПОЛНЯЕТСЯ, но амплитудные значения тока и напряжения подчиняются закону Ома:								.

РИС.133

РИС.134

РИС.135

Полученные соотношения отчетливо проявляются на графиках зависимости силы тока и напряжения от времени (рис.134), а также на векторной диаграмме (рис.135).

ИНДУКТИВНАЯ НАГРУЗКА.

Рассмотрим участок цепи с катушкой индуктивности L и пренебрежимо малыми активным сопротивлением и емкостью

(рис.136). Пусть по участку протекает ток i = Im sin ωt .
Так как ЭДС самоиндукции, согласно правилу Ленца,	препятствует	изменению протекающего тока, то
uL = −εci = L di = LωIm cosωt = LωIm sin(ωt +	π ) =ULm sin(ωt +		π )
dt	2		2 .

Следовательно, напряжение на индуктивности совершает гармонические колебания с той же частотой, что и сила тока, но

π

опережает по фазе силу тока на	2 (по времени – на четверть периода). Амплитудные значения силы тока и напряжения
	Im	=	ULm	=	ULm
			X L		ωL , где X L = ωL - называется
также связаны соотношением,	аналогичным закону Ома:

индуктивным сопротивлением.

Графики зависимости силы тока и напряжения, а также векторная диаграмма, представлены на рис.137 и рис.138.

РИС.136 РИС.137 РИС.138

§ 52 ПОСЛЕДОВАТЕЛЬНАЯ ЦЕПЬ ПЕРЕМЕННОГО ТОКА СО СМЕШАННОЙ НАГРУЗКОЙ.

Рассмотрим участок цепи, состоящий из последовательно соединенных активного сопротивления, конденсатора емкостью

С и катушки с индуктивностью L (рис.139), по которому течет ток i = Im sin ωt .

В случае квазистационарного тока, согласно закону сохранения энергии, общее мгновенное напряжение на этом участке будет складываться из мгновенных напряжений на каждом из последовательно включенных элементов:

u = uR + uC + uL = U Rm sin ωt + U Cm sin( ωt − π2 ) + U Lm sin( ωt + π2 ) .

Так как складываемые напряжения представляют собой гармонические колебания одной частоты, то и мгновенное напряжение также будет изменяться с такой же частотой.

57

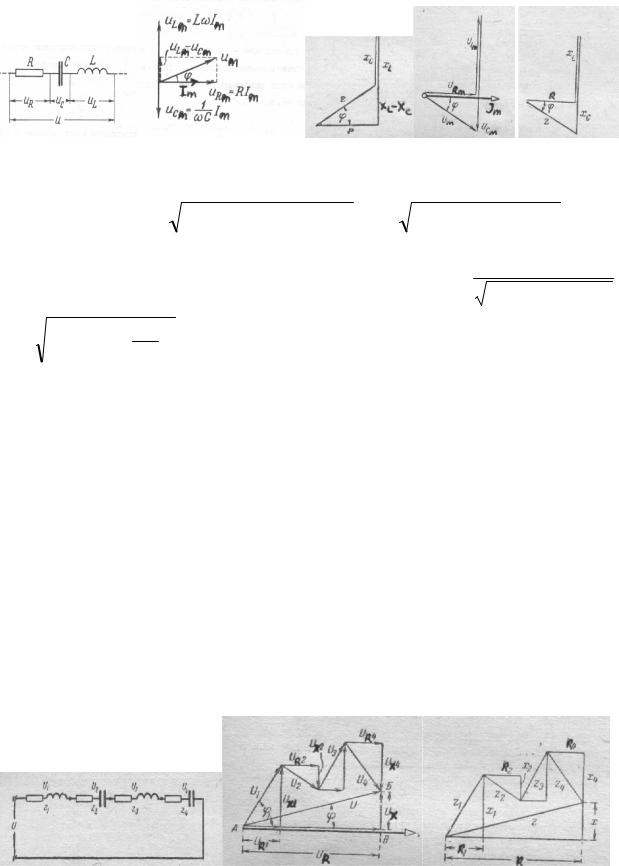
Рассчитать амплитудное значение этого напряжения и сдвиг фаз по отношению к силе тока можно двумя способами: используя тригонометрические формулы для суммы и разности или методом векторных диаграмм (рис.140). Воспользуемся методом векторных диаграмм.

РИС.139	РИС.140	РИС.141 РИС.142 РИС.143
Построив вектор-амплитуду		результирующего напряжения	как векторную сумму амплитуд напряжений на всех
	Um = URm2 + (ULm −UCm )2		= Im R2 + ( X L − X C )2
элементах, получим:

Следовательно, и в случае смешанного последовательного соединения различных нагрузок, амплитудные значения силы тока

Im	=	Um
		+ ( X		− X		)2
и общего напряжения связывает соотношение аналогичное закону Ома:	R2		L		C
						, где

Z = R2 + (ωL −

1

)2

ωC

представляет собой полное сопротивление (импеданс) данного участка цепи.

Как видно из рис.140, суммарное мгновенное напряжение сдвинуто по фазе относительно силы тока и изменяется

соответственно по закону

u =Um sin(ωt +ϕ) . Сдвиг фаз можно определить с помощью векторной диаграммы:

ULm −UCm

X L

− X C

ωL −

1

tgϕ

=

=

=

ωC

URm

R

R

. Из этой формулы следует, что в зависимости от соотношения

индуктивного и емкостного сопротивлений участка цепи общее мгновенное напряжение может как опережать, так и отставать по фазе от мгновенной силы тока.

Важно отметить, что, хотя мгновенные значения напряжений складываются, полное сопротивление цепи не является арифметической суммой активного, емкостного и индуктивного сопротивлений.

Разность индуктивного и емкостного сопротивлений называется реактивным сопротивлением цепи: X = X L − X C . Эта величина может быть положительной или отрицательной, что по физическому смыслу будет определять опережение или отставание по фазе напряжение от силы тока в цепи. Следствием последовательного соединения элементов

цепи и векторной диаграммы напряжений является «треугольник» сопротивлений.

Полное сопротивление в этом прямоугольном треугольнике представляет собой гипотенузу, а катеты – это активное и реактивное сопротивления.

На рис. 141 треугольник сопротивлений в цепи с положительным реактивным сопротивлением. На рис.142 и рис.143 показаны векторная диаграмма и треугольник сопротивления для цепи «емкостного» характера, т.е. реактивное сопротивление в этом случае отрицательно.

На рис.144 представлен один из многочисленных вариантов общего случая последовательного соединения различных элементов.

РИС.144

РИС.145

РИС.146

58