2.2. Важливі границі

 

1) Перша важлива границя

Розглянемо функцію . Значення цієї функції при  не існує, але .

Теорема 2.1. Справедлива рівність

 

.                                         (2.4)

 

Границю (2.4) називають першою важливою (першою чудовою) границею.

Доведення. Нехай  (x вимірюється в радіанах).

 

Рис. 2.3

Розглянемо рис. 2.3, на якому позначено , , , . Виходячи з геометричних міркувань матимемо:   ; ;   .

Оскільки , то, поділивши останню нерівність на , матимемо:

 або .

 

Знайдемо ,

.

Отже,

 

.

 

У випадку  доведення проводиться аналогічно. Тут маємо:

.

 

Об’єднаємо отримані результати:

 

.

 

Графік функції  має вигляд (рис. 2.4).

Рис. 2.4

2) Друга важлива границя

Теорема 2.2. Функція 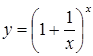 при  має границею число , тобто

.                                          (2.5)

 

Границю (2.5) називають другою важливою (другою чудовою) границею.

(Зауважимо, що числом  прийнято позначати границю такої збіжної послідовності: , це число є ірраціональним (irrational) .)

Доведення. Розглянемо випадок, коли . Нехай

 

.

 

Піднесемо члени отриманої нерівності до степенів, показники яких є частинами нерівності . Дістанемо

 

.

 

Перейдемо до границі при . Оскільки

 

,

,

 

то

.

 

Аналогічно доводиться справедливість рівності .

Зауваження. Якщо , то . Поклавши  , матимемо іншу форму запису другої важливої границі

 

.                                        (2.6)

 

Натуральний логарифм. Логарифм числа x за основою e називається натуральним логарифмом і позначається .

 

2.3. Нескінченно малі (н. М.) і нескінченно великі (н. В.) функції та зв’язок між ними

 

Означення 2.6. 1) Послідовність  називається нескінченно малою, якщо

.

 

2) Функція  називається нескінченно малою функцією (infinitesimal function) (або просто н. м.) в точці  (або при ), якщо

.

Аналогічні означення н. м. при , , , , , .

Для спрощення процесу доведення сформулюємо та доведемо властивості нескінченно малих для випадку послідовностей.

Теорема 2.3. Якщо , то  є нескінченно малою.

Доведення. За означенням границі послідовності маємо:

 

.

 

Оскільки , то

.

Це означає, що  і  – нескінченно мала.

Теорема 2.4. Якщо  – нескінченно мала, то .

Доведення. Оскільки  – нескінченно мала, то за означенням 2.6 маємо:

 

,

або

 

.

 

Згідно з означенням границі числової послідовності одержуємо, що .

Теорема 2.5. Алгебраїчна сума (добуток) скінченного числа нескінченно малих послідовностей є нескінченно малою.

Доведення. Доведемо теорему, наприклад, для випадку суми двох нескінченно малих послідовностей  та . Маємо:

 

;

 

.

 

За  оберемо  та оцінимо модуль :

 

.

 

         Таким чином,

 

.

 

 

Теорема 2.6. Добуток нескінченно малої послідовності на послідовність обмежену є нескінченно малою послідовністю.

Доведення. Нехай  – обмежена послідовність, тоді існує таке число , що для всіх номерів  виконується нерівність .

Якщо , то .

Оцінимо модуль , маємо:

 

.

 

Таким чином,

 

.

Зауваження. Частка від ділення нескінченно малої послідовності на послідовність, яка має відмінну від нуля границю, є величина нескінченно мала.

 

Запам’ятай добре! Усі перераховані вище властивості мають місце і для нескінченно малих функцій.

 

Означення 2.7. 1) Послідовність  називається нескінченно великою, якщо

 

,

тобто, , де  – як завгодно велике додатне число.

2) Функція  називається нескінченно великою функцією (infinite function) (або просто н. в.) в точці  (або при ), якщо:

 

.

 

Символічно це записують так:

 

.

 

Якщо ж виконується нерівність  , то пишуть

 

      ().

 

Аналогічно визначаються границі:

 

,    .

 

Мають місце теореми.

Теорема 2.7

1)    Алгебраїчна сума нескінченно великих послідовностей (функцій) одного знака є нескінченно великою;

2)    добуток нескінченно великих послідовностей (функцій) є нескінченно великим.

 

Зв’язок між н. в. та н. м. розкриває наведена нижче теорема, сформульована для послідовностей.

Теорема 2.8

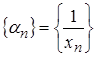1)    Якщо  – нескінченно велика послідовність, то послідовність  є нескінченно малою;

2)    Якщо  – нескінченно мала послідовність, то послідовність  є нескінченно великою.

Доведення. 1) Якщо  – нескінченно велика послідовність, то

 

.

Тоді . Оскільки  – як завгодно велике додатне число, то число  є як завгодно малим, тому

.

 

2) Якщо  – нескінченно мала послідовність, то

 

.

Тоді 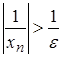. Оскільки  – як завгодно мале додатне число, то число  є як завгодно великим, тому

.