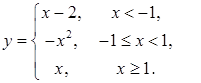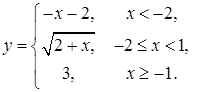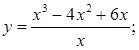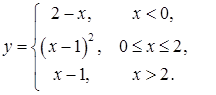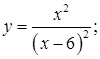Завдання для самостійної роботи

 

Завдання 2.1. Знайти границі функцій.

1. , , , , , , , , , .

2. , , , , , , , , , .

3. , , , , , , , , , .

4. , , , , , , , , , .

5. , , , , , , , , , .

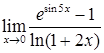6. , , , , , , , , , .

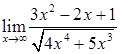7. , , , , , , , , , .

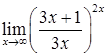8. , , , , , , , , , .

9. , , , , , , , , , .

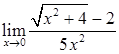10. , , , , , , , , , .

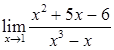11. , , , , , , , , , .

12. , , , , , , , , , .

13. , , , , , , , , , .

14. , , , , , , , , , .

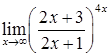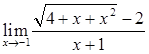15. , , , , , , , , , .

16. , , , , , , , , , .

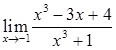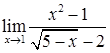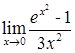17. , , , , , , , , , .

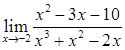18. , , , , , , , , , .

19. , , , , , , , , , .

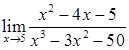20. , , , , , , ,, , .

21. , , , , , , , , , .

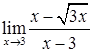22. , , , , , , , , , .

23. , , , , , , , , , .

24. , , , , , , , , , .

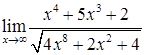25. , , , , , , , , ,.

26. , , , , , , , , , .

27. , , , , , , , , , .

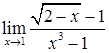28. , , , , , , , , , .

29. , , , , , , ,, , .

30. , , , , , , , , , .

31. , , , , , , , , , .

32. , , , , , , ,, , .

33. , , , , , , , , , .

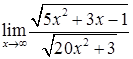34. , , , , , , , , , .

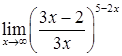35. , , , , , , , , , .

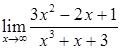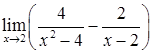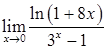36. , , , , , , , , , .

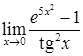37. , , , , , , , , , .

38. , , , , , , ,, , .

39. , , , , , , , , , .

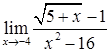40. , , , , , , , , , .

41. , , , , , , , , , .

42. , , , , , , , , ,.

43. , , , , , , , , , .

44. , , , , , , , , , .

45. , , , , , , , , , .

46. , , , , , , , , , .

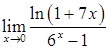47. , , , , , , , , , .

48. , , , , , , , , , .

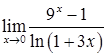49. , , , , , , , , , .

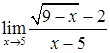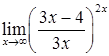50. , , , , , , , , , .

 

Завдання 2.2. Дослідити функцію на неперервність, визначити характер її точок розриву.

 

1.
2.
3.
4.
5.
6.
7.
8.
9.			;
10.		;
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.	;
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.

Тема 3. Диференціальне числення функції однієї змінної

 

3.1. Похідна функції

 

Нехай функція  визначена на деякому проміжку Х і точка . Надамо аргументу функції приросту  (або ) такого, щоб точка . Функція дістане при цьому приріст

 

.

 

Складемо відношення

 

.

 

Означення 3.1. Відношення приросту функції до приросту аргументу називається середньою швидкістю зміни функції (rate of change of function).

Це відношення показує, скільки одиниць приросту функції припадає на одиницю приросту аргументу.

 

Означення 3.2. Границя відношення приросту функції до приросту аргументу за умови, що приріст аргументу прямує до нуля, називається швидкістю зміни функції в даній точці або її похідною(derivative) і позначається одним із символів:

 

.

Отже, за означенням

 

.                (3.1)

 

Якщо похідна функції  в точці  існує, то функція називається диференційовною(differentiable function) в точці .

Якщо функція диференційовна в кожній точці деякого проміжку Х, то вона називаєтьсядиференційовною на проміжку Х.

Операція відшукання похідної називається диференціюванням.

 

Приклад 3.1. Користуючись означенням похідної, знайти похідну функції .

Розв’язання. Знайдемо приріст даної функції в точці .

 

,

 

звідки

,

 

оскільки ;  при , то

.

 

Остання формула справедлива для будь-якого , тому запишемо її так:

.                                         (3.2)

 

Відмітимо, що цілком аналогічно можна вивести формулу

 

.                                      (3.3)

 

 

Геометричний зміст похідної (geometric sense of derivative)

Похідна функції  в точці  дорівнює кутовому коефіцієнту дотичної (tangent line) до графіка даної функції у точці , тобто

 

,                                      (3.4)

 

де  -кут, який утворює дотична  з додатним напрямком осі 

(рис. 3.1).

 

Рис. 3.1

 

Приклад 3.2. Користуючись означенням похідної, знайти похідну функції  у точці  і з’ясувати зміст одержаного результату.

Розв’язання. Знайдемо приріст даної функції в точці .

 

.

Звідки .

 

Отже .

 

Якщо , то . Це означає, що в даній точці функція спадає з такою ж самою швидкістю, з якою зростає аргумент.

З геометричного погляду , звідки  - кут, який утворює дотична , проведена до параболи у точці  (рис. 3.2).

 

Рис. 3.2

Зв’язок між диференційовністю функції та її неперервністю

Для існування границі (3.1) необхідно, щоб  (). Тому функція повинна бути неперервною. Але не завжди існує границя (3.1) для неперервної функції. Ця умова не є достатньою а лише необхідною умовою диференційовності.

 

Приклад 3.3 . Чи існує ?

Розв’язання. Функція  неперервна на всьому проміжку , проте в точці  вона не має похідної. Дійсно:

якщо , то ;

якщо , то .

Отже, в цій точці  функція  не має похідної.

 

Теорема 3.1. Якщо функція  диференційовна в точці , то вона неперервна в цій точці.

Доведення. Нехай існує . За означенням похідної . Також ми маємо , де   - нескінченно мала при . Тоді , якщо . Отже, ми довели, що  неперервна в точці  (за означенням).

 

3.2 Правила диференціювання (Table of Derivative Rule)

 

Теорема 3.2. Якщо функції  і  мають похідні в точці x, то справедливі формули для похідних суми, добутку та частки цих функцій:

 

1)  - (Sum Rule);

 

2)  - (Product Rule);

 

3) , при  - (Quotient Rule).

Доведення. 1) Дійсно, розглянемо похідну суми даних функцій:

 

 

, що і потрібно було довести.

 

2) Розглянемо похідну добутку даних функцій:

 

 

 

,

що і потрібно було довести (тут використано, що , оскільки диференційовна функція  - неперервна).

 

3) Розглянемо похідну частки даних функцій за умови, що :

 

,

що і потрібно було довести.

 

Зауваження. Сталий множник при диференціюванні виноситься за знак похідної (ConstantMultiple Rule), тобто:

 

, де .

Приклад 3.4. Знайти похідну функції .

Розв’язання. За означенням функція  визначена при . Знайдемо похідну частки за теоремою 3.2, використовуючи формули (3.2), (3.3):

.

Отже, при  маємо:

.                                       (3.5)

 

Похідна складеної функції (Chain Rule)

Нехай функція  визначена в деякому околі точки  і функція  визначена в деякому околі точки , таким чином визначена складена функція .

Теорема 3.3. Якщо функція  має похідну в точці  і функція  має похідну в точці , то складена функція  також має похідну в точці , причому

 

,                              (3.6)

або скорочено

                                         (3.6*)

 

Доведення. За означенням маємо:

 

.

 

Приклад 3.5. Знайти похідну функції .

Розв’язання. Приймаючи , маємо:

 

 

Тут враховано, що  також складена функція і тому за формулою (3.6) вона має похідну .

 

Похідна оберненої функції (derivative of inverse function)

Теорема 3.4. Якщо функція , ,  має обернену  і для всіх  існує похідна , то для всіх  існує похідна , причому справедлива рівність:

 

 або , .                    (3.7)

 

Доведення. З означення похідної маємо:

, тобто , .

 

Приклад 3.6. Знайти похідну функції, оберненої до функції .

Розв’язання. Функція  неперервна і монотонна на проміжку . Отже, на цьому проміжку існує обернена функція, яку позначають , , 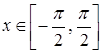. Нагадаємо, що графіки обернених функцій симетричні відносно прямої  (рис. 3.3).

 

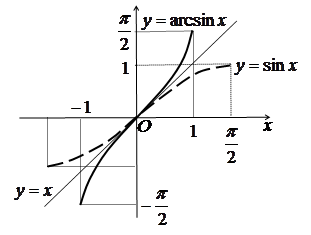
Рис. 3.3

Знаходимо похідну . Оскільки аргументом оберненої функції є y, то виконаємо такі перетворення:

,

 

знак «+» взято, оскільки при  . Отже  або

 

.

 

Якщо аргументом є змінна х, то маємо формулу

 

.                           (3.8)

 

Продовжуючи знаходити похідні базисних елементарних функцій з урахуванням означення похідної, її властивостей та правил диференціювання можна скласти наведену нижче таблицю.
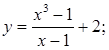
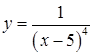