
- •Тема 1. Вступ до математичного аналізу
- •1.1. Поняття функції
- •1.2. Побудова графіків функцій шляхом елементарних перетворень
- •Тема 2. Елементи теорії границь
- •2.1. Границя послідовності та границя функції
- •2.2. Важливі границі
- •2.3. Нескінченно малі (н. М.) і нескінченно великі (н. В.) функції та зв’язок між ними
- •2.4. Порівняння н. М. Функцій
- •2.5. Основні теореми про границю
- •2.6. Техніка обчислення границь
- •2.8. Неперервність функції
- •Завдання для самостійної роботи
- •Тема 3. Диференціальне числення функції однієї змінної
- •3.1. Похідна функції
- •Таблиця похідних основних елементарних функцій
- •3.3. Диференціал функції
- •3.4 Похідні та диференціали вищих порядків
2.8. Неперервність функції
Означення
2.8. Функція ![]() називається неперервною в
точці
називається неперервною в
точці ![]() (continuous function at point),
якщо:
(continuous function at point),
якщо:
1) вона визначена в цій точці і в деякому її околі;
2) нескінченно малому приростові аргументу відповідає нескінченно малий приріст функції:
![]() ,
або
,
або ![]() .
(2.7)
.
(2.7)
Приклад
2.30. Дослідити
на неперервність функцію ![]() в
точці
в
точці ![]() .
.
Розв’язання.
![]()
![]()

Якщо ![]() ,
то
,
то ![]() ;
;  - величина
обмежена, тому, за теоремою 2.4,
- величина
обмежена, тому, за теоремою 2.4, ![]() .
Отже,
.
Отже, ![]() ,
і тому, за означенням 2.8, функція
,
і тому, за означенням 2.8, функція ![]() - неперервна
в точці
- неперервна
в точці ![]() .
.
Неперервність функції в точці можна означити і по-іншому.
Означення
2.9. Функція ![]() називається неперервною
в точці
називається неперервною
в точці ![]() ,
якщо вона має в цій точці границю, яка
дорівнює значенню функції в точці
,
якщо вона має в цій точці границю, яка
дорівнює значенню функції в точці ![]() ,
тобто
,
тобто
![]() .
(2.8)
.
(2.8)
Рівність
(2.8) можна деталізувати: границя зліва
в точці ![]() має
дорівнювати границі справа і дорівнювати
значенню функції в цій точці:
має
дорівнювати границі справа і дорівнювати
значенню функції в цій точці:
![]() .
(2.8*)
.
(2.8*)
Означення
2.10. Функція ![]() називається неперервною
на проміжку (continuous function oninterval),
якщо вона неперервна в кожній точці
цього проміжку.
називається неперервною
на проміжку (continuous function oninterval),
якщо вона неперервна в кожній точці
цього проміжку.
Арифметичні операції над неперервними функціями приводять знову до неперервних функцій.
Теорема
2.19. Якщо
функції ![]() і
і ![]() є
неперервними в точці
є
неперервними в точці ![]() ,
тоді неперервними в цій точці будуть
також функції:
,
тоді неперервними в цій точці будуть
також функції:
1) ![]() ,
, ![]() ;
;
2) ![]() ;
;
3)  за
додаткової умови
за
додаткової умови ![]() .
.
Доведення. Нехай
функції ![]() ,
, ![]() -неперервні
в точці
-неперервні
в точці ![]() .
Тоді, за означенням 2.9,
.
Тоді, за означенням 2.9, ![]() ,
, ![]() .
Використаємо теореми про арифметичні
операції над функціями, що мають границю:
.
Використаємо теореми про арифметичні
операції над функціями, що мають границю:
1) ![]() ;
;
2) ![]() ;
;
3)  .
.
Бачимо, що означення 2.9 виконується в кожному з цих випадків. Тобто ми показали, що при виконанні арифметичних дій над неперервними функціями ми знову отримаємо неперервні функції.
Неперервність складеної функції
Теорема
2.20. Якщо
функція ![]() неперервна
в точці
неперервна
в точці ![]() ,
а функція
,
а функція ![]() неперервна
в точці
неперервна
в точці ![]() ,
то складена функція
,
то складена функція ![]() неперервна
в точці
неперервна
в точці ![]() .
.
Доведення. Справді,
оскільки функція ![]() неперервна
в точці
неперервна
в точці ![]() ,
то
,
то ![]() ;
; ![]() -неперервна
в точці
-неперервна
в точці ![]() ,
тому
,
тому ![]() .
А це означає, що функція
.
А це означає, що функція ![]() неперервна
в точці
неперервна
в точці ![]() .
.
Властивості функцій, неперервних на відрізку
Теорема
2.21. (Вейєрштрасса).
Якщо функція ![]() неперервна
на відрізку
неперервна
на відрізку ![]() ,
то вона:
,
то вона:
1) обмежена (bounded function) на цьому відрізку;
|
| |
|
|
|
2)
досягає на цьому відрізку свого
найбільшого ![]() та
найменшого
та
найменшого ![]() значень
(рис. 2.6).
значень
(рис. 2.6).
![]() ,
, ![]() ;
; ![]() .
.
Рис. 2.6
Теорема
2.22. (Больцано - Коші).
Якщо функція ![]() неперервна
на відрізку
неперервна
на відрізку ![]() і
і ![]() ,
то всередині відрізка існує принаймні
одна точка с,
в якій функція набуває рівного С значення
(рис. 2.7).
,
то всередині відрізка існує принаймні
одна точка с,
в якій функція набуває рівного С значення
(рис. 2.7).
![]() .
.

Рис. 2.7
Наслідок з
теореми Больцано - Коші.
Якщо функція ![]() неперервна
на відрізку
неперервна
на відрізку ![]() і
в його кінцевих точках набуває різних
за знаком значень, то всередині відрізка
існує принаймні одна точка, в якій
значення функції дорівнює нулю (рис.
2.8).
і
в його кінцевих точках набуває різних
за знаком значень, то всередині відрізка
існує принаймні одна точка, в якій
значення функції дорівнює нулю (рис.
2.8).

![]()
Рис. 2.8
Точки розриву функції та їх класифікація
Означення
2.11. Якщо
функція ![]() в
точці
в
точці ![]() не
є неперервною, то точка
не
є неперервною, то точка ![]() називаєтьсяточкою
розриву функції
(discontinuity point).
називаєтьсяточкою
розриву функції
(discontinuity point).
Зауваження. Елементарна функція не може мати розривів у внутрішніх точках своєї області визначення.
Точки розриву функції можна поділити на види:
· Точки розриву першого роду (ordinary discontinuity).
Означення
2.12. Точка ![]() називається точкою
розриву функції
називається точкою
розриву функції ![]() першого
роду,
якщо існують скінченні односторонні
границі при
першого
роду,
якщо існують скінченні односторонні
границі при ![]() ,
але вони не рівні між собою.
,
але вони не рівні між собою.
![]() - точка
розриву першого роду
- точка
розриву першого роду 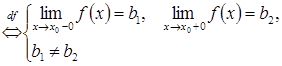 .
.
Приклад
2.31. Дослідити
на розрив функцію  .
.
Розв’язання. Оскільки ![]() не
існує, то
не
існує, то ![]() - точка
розриву функції.
- точка
розриву функції.
Обчислимо
односторонні границі функції в точці ![]() :
:
![]() ,
, ![]() .
.
Оскільки ![]() ,
то точка
,
то точка ![]() є
точкою розриву першого роду.
є
точкою розриву першого роду.
Графік даної функції подано на рисунку 2.9.

Рис. 2.9
· Точки розриву другого роду (no ordinary discontinuity).
Означення
2.13. Точка ![]() називається точкою
розриву функції
називається точкою
розриву функції ![]() другого
роду,
якщо хоч би одна з односторонніх границь
(зліва чи справа) при
другого
роду,
якщо хоч би одна з односторонніх границь
(зліва чи справа) при ![]() не
існує (зокрема, дорівнює нескінченності
(infinite discontinuity)).
не
існує (зокрема, дорівнює нескінченності
(infinite discontinuity)).
Приклад
2.32. Дослідити
на розрив функцію ![]() .
.
Розв’язання. Оскільки ![]() не
існує, то
не
існує, то ![]() - точка
розриву функції.
- точка
розриву функції.
Обчислимо
односторонні границі функції в точці ![]() :
:
 ,
(оскільки
,
(оскільки  );
);
 ,
(оскільки
,
(оскільки  ).
).
Оскільки ![]() не
існує, то точка
не
існує, то точка ![]() є
точкою розриву другого роду.
є
точкою розриву другого роду.
Для
схематичної побудови графіка функції,
окрім односторонніх границь в точці ![]() ,
знайдемо границю при
,
знайдемо границю при ![]() :
:
|
Рис. 2.10 |
(оскільки
А
це означає, що пряма Графік даної функції подано на рисунку 2.10.
|
· Точки усувного розриву (removable discontinuity, removable jump).
Означення
2.14. Точка ![]() називається точкою
усувного розриву функції
називається точкою
усувного розриву функції ![]() ,
якщо в цій точці виконується умова
,
якщо в цій точці виконується умова ![]() ,
але або
,
але або ![]() ,
або
,
або ![]() не
існує.
не
існує.
Приклад
2.33. Дослідити
на розрив функцію  .
.
Розв’язання. Оскільки ![]() не
існує, то
не
існує, то ![]() - точка
розриву функції.
- точка
розриву функції.
Обчислимо
границі зліва і справа в точці ![]() :
:
 ,
,
 .
.
Оскільки ![]() ,
то точка
,
то точка ![]() є
точкою усувного розриву.
є
точкою усувного розриву.
Отже
маємо: 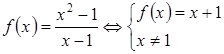 .
.
Схематичний графік зображено на рисунку 2.11.

Рис. 2.11
Приклад
2.34. Дослідити
функцію  і
визначити вид точок розриву, якщо вони
є. Зробити схематичний рисунок.
і
визначити вид точок розриву, якщо вони
є. Зробити схематичний рисунок.
Розв’язання. Дана
функція визначена для всіх ![]() .
Оскільки
.
Оскільки ![]() не
існує, то
не
існує, то ![]() -точка
розриву функції.
-точка
розриву функції.
Обчислимо
односторонні границі в точці ![]() :
:
 ,
(т. як
,
(т. як  );
);
 ,
(т. як
,
(т. як ![]() ).
).
Оскільки
границі ![]() ,
, ![]() існують,
проте
існують,
проте ![]() ,
то точка
,
то точка ![]() є
точкою розриву першого роду.
є
точкою розриву першого роду.
В
точці ![]() функція
має стрибок, що дорівнює різниці
функція
має стрибок, що дорівнює різниці
![]() .
.
Для
схематичної побудови графіка функції
знайдемо її границю при ![]() :
:
 ,
(т. як
,
(т. як  ).
).
А
це означає, що пряма ![]() є
горизонтальною асимптотою.
є
горизонтальною асимптотою.
Схематичний графік даної функції зображено на рис. 2.12.

Рис. 2.12
Приклад 2.35. Дослідити задану функцію на неперервність і визначити рід точок розриву, якщо вони є. Зробити схематичний рисунок.

Розв’язання. Маємо
неелементарну функцію, що неперервна
на кожному з інтервалів: ![]() .
Очевидно, що вона може бути розривною
лише в точках
.
Очевидно, що вона може бути розривною
лише в точках ![]() ,
, ![]() ,
в яких змінюється аналітичний вираз,
що задає функцію. Перевіримо умови
неперервності в цих точках.
,
в яких змінюється аналітичний вираз,
що задає функцію. Перевіримо умови
неперервності в цих точках.
1)
Розглянемо точку ![]() .
.
Функція
визначена в цій точці і ![]() .
.
![]() ,
, ![]() .
.
Отже,
існують односторонні границі функції
в точці ![]() ,
але вони не рівні між собою. А це означає,
що дана точка є точкою розриву першого
роду.
,
але вони не рівні між собою. А це означає,
що дана точка є точкою розриву першого
роду.
2)
Розглянемо точку ![]() .
.
Функція
визначена в цій точці і ![]() .
.
![]() ,
, ![]() .
.
Отже,
існують односторонні границі функції
в точці ![]() ,
вони рівні між собою і дорівнюють
значенню функції в цій точці:
,
вони рівні між собою і дорівнюють
значенню функції в цій точці: ![]() .
Це означає, що в даній точці функція
неперервна.
.
Це означає, що в даній точці функція
неперервна.
Зробимо схематичний рисунок (рис. 2.13).

Рис. 2.13



 ,
,