2.4. Порівняння н. М. Функцій

 

Нехай функції  - н. м. при , тобто  і . Складемо відношення .

1. Якщо , то  називається н. м. вищого порядку (high order infinitesimal) (н. м. вищого порядку малості), ніж  при . Це записують так:  („o” маленьке від ).

2. Якщо , то  і  називаються н. м. одного порядку (equal orderinfinitesimals) при . Це записують так:  („O” велике від ).

3. Якщо 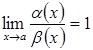, то  і  називаються еквівалентними н. м. (equivalent infinitesimal) при . Це записують так: .

 

Таблиця еквівалентних н. м. функцій ().

 

,	,
,	,
,	,
,	,
,	.

 

Теорема 2.9. Н. м. функції  і  будуть еквівалентними () при  тоді і тільки тоді, коли їх різниця  є

н. м. вищого порядку, ніж н. м.  і  при.

Доведення. Необхідність. Нехай н. м.  (або ) при . Доведемо, що їх різниця  є н. м. вищого порядку, ніж н. м.  і  при. Для цього розглянемо границю:

 

.

А отже  є н. м. вищого порядку, ніж н. м.  при.

 

Достатність. Доведемо, що якщо різниця  є н. м. вищого порядку, ніж н. м.  при, то . Дійсно

,

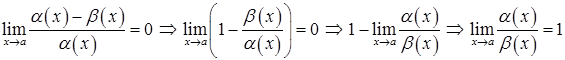тому при . Цілком аналогічно доводиться, що якщо різниця  є н. м. вищого порядку, ніж н. м.  при , то .

 

Теорема 2.10. Якщо н. м. ,  при , то справедлива рівність

.

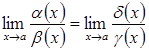Доведення. Дійсно

 

.

 

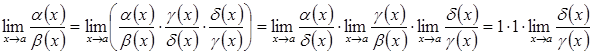Зауваження. Теорема 2.10 дає можливість замінювати під знаком границі н. м. множники та дільники на еквівалентні (н. м. доданки замінювати на еквівалентні в загальному випадку не можна).

При порівнянні нескінченно великих (н. в.) функцій мають місце аналогічні правила порівняння. Наприклад, дві н. в. функції  і  називаються еквівалентними (equivalent) при , якщо

.

 

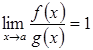Так, при  має місце еквівалентність:

 

,

тому при обчисленні границі відношення двох многочленів на нескінченності ми можемо замінити вираз під знаком границі на еквівалентне відношення старших степенів многочленів, взятих зі своїми коефіцієнтами.

2.5. Основні теореми про границю

 

Теорема 2.11. Границя сталого дорівнює сталому, тобто

, де .

Доведення. Нехай , де . Розглянемо різницю , маємо:  – нескінченно мала величина. За теоремою 2.4 маємо, що .

 

Теорема 2.12. Границя суми дорівнює сумі границь.

 

Доведення. Нехай, наприклад, , . Покажемо, що . Дійсно

;

 

.

 

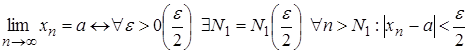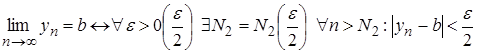За  оберемо  та оцінимо модуль , маємо:

.

Таким чином,

 

.

Зауваження. Випадок суми довільного скінченного числа числових послідовностей доводиться аналогічно.

 

Теорема 2.13. Границя добутку дорівнює добутку границь.

 

Доведення. Нехай, наприклад, , . Покажемо, що . Дійсно, якщо , то за теоремою 2.3 , де  – нескінченно мала величина. Аналогічно, , де  – нескінченно мала. Тоді

 

.

 

Оскільки константа є величиною обмеженою, то за теоремою 2.6 величини  є нескінченно малими; за теоремою 2.5 величина  також є нескінченно малою. Оскільки сума трьох нескінченно малих величин є нескінченно малою, то  є нескінченно мала і за теоремою 2.4.

 

Зауваження

1)    Сталий множник можна виносити за знак границі.

 

Дійсно,

.

 

 

2) .

Дійсно,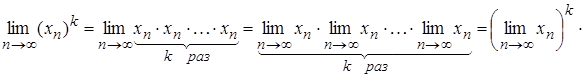

 

 

3) .

 

 

Теорема 2.14. Границя частки двох послідовностей дорівнює частці границь цих послідовностей, якщо границя знаменника не дорівнює нулю, тобто

, де .

 

 

Зауваження. Доведення даної теореми проводиться аналогічно доведенню теореми 2.13.

 

Теорема 2.15.

1) , де ;

2) , де .

Теорема 2.16. Якщо для послідовності  відомо, що для всіх  і , то .

Доведення. Проведемо доведення методом від супротивного. Нехай , але тоді  і . Остання рівність суперечить умові теореми. Це означає, що наше припущення хибне і .

 

Теорема 2.17. Якщо для послідовностей  та  відомо, що , то .

Доведення. За умовою теореми , тоді за теоремою 2.16

 

.

 

Теорема 2.18. .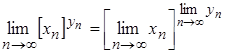

 

Запам’ятай добре! Аналогічні теореми мають місце для границь функцій в точці.