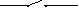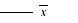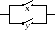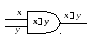§ 8. Некоторые применения алгебры высказываний
Анализ логических рассуждений. Рассмотрим несколько примеров, которые используют понятие логического следования.
Примеры: 1. Правильно ли следующее логическое рассуждение: “Когда выпадает снег, птицы улетают на юг. Если птицы улетели на юг, то скоро наступит зима. Зима наступила. Следовательно, либо выпал снег, либо птицы улетели на юг”.
|
a |
b |
c |
a b |
b c |
b a |
|
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
b
a.
Проверим, так ли это, по таблице
истинности. Как видно из таблицы, формула
b
a
не является логическим
следствием формул a
b,
b
c,
с: именно, она ложна при
a
= 0 = b,
c
= 1, когда все посылки
рассматриваемого логического следования
истинны. Другими словами, в ситуации,
когда зима наступила, но снег не выпал
и птицы не улетели на юг, приведённый
вывод не корректен.2. Оцените правильность логического вывода: “Если a < b, то b – a > 0. Если a b, то a – b 0. Либо a < b, либо a – b 0. Следовательно, либо неверно, что a – b < 0, либо неверно, что b – a 0”.
Обозначая
элементарные высказывания буквами,
получим: x
:= “a
< b”,
y
:= “b
– a
> 0”, z
:= “a
b”,
t
:= “a
– b
0”. Тогда
=
“a
– b
< 0”,
=
“b
– a
0”, и нужно
схема рассуждения x
y,
z
t,
x
t
,т.е.
x
y,
z
t,
x
t
t
y.
Формула t
y
ложна только
при t
= 0 = y,
но при этих значениях все три формулы
x
y,
z
t,
x
t
не могут
быть одновременно истинны: для формулы
x
t
условие
истинности при t
= 0 означает
x
= 1, что влечёт
ложность значения формулы x
y.
Итак, заключение не может быть ложным
при истинности всех посылок, т.е.
рассуждение правильное.
Замечание: С точки зрения математики в целом все посылки и заключение в исследованном рассуждении истинны.
3. Оцените правильность логического вывода: “Если число, составленное из двух младших цифр числа чётно, то само число делится на 2. Если сумма всех цифр числа делится на 3, то само число делится на 3. Сумма цифр трёхзначного числа равна 27. Число 27 делится на 3. Значит, это трёхзначное число не делится на 2”.
Аналогично предыдущему, a := “число, составленное из двух младших цифр числа n чётно”, b := “число n делится на 2”, c := “сумма всех цифр числа n делится на 3”, d := “число n делится на 3”, e := “число n трёхзначно”, f := “сумма цифр числа n равна 27”, g := “27 делится на 3”.
Исследуем логическое
следование a
b,
c
d,
e
f,
g
e
.
Очевидно, что в таком общем виде оно не
имеет места (?!), хотя рассматриваемое
рассуждение верно с общематематической
точки зрения: если при сформулированных
условиях
2, то цифра
z
чётна, и x
+ y
+ z
= 27 влечёт
x
= y
= z
= 9 – противоречие.
Однако, с точки зрения логики, в этом верном математическом рассуждении есть пробелы: заключение невозможно вывести из сформулированных посылок, используя только правила логического вывода – мы привлекли для обоснования заключения арифметическое свойство трёхзначных чисел. Этот пример показывает, что математика не сводится к логике, хотя и не может без неё обойтись. Придумайте более простые примеры, иллюстрирующие этот вывод.
Оптимизация логики условных переходов в программах. В сложных программах может использоваться много логических переменных, которые, причудливо сплетаясь и нагромождаясь друг на друга в условных операторах, способны запутать даже опытного программиста.
Примеры. 1. Следующий фрагмент программы чудовищен:
if (not(a and b) or (a or b)) then
P
else
if (not(a or b) and not(b)) then
Q
else
R;
Действительно, стоит только упростить логическое выражение
(a
b)
a
b
a
b
1,
как выяснится, что никаких условных операторов вообще не нужно: приведённый фрагмент программы равносилен просто выполнению группы операторов P.
2. Не лучше и такой фрагмент:
if (not(a and b) or (not(a or с) and not(b) and c)) then
P
else
if (not(a or b) and not(b or c)) then
Q
else
R;
Первое условие – для группы операторов P – оптимизируется так:
(
c)
(
c)
(
c)
.
Условие для группы операторов Q таково:
a
b
a
b
0,
так что операторы группы Q не выполняются никогда, а условие для группы операторов R принимает вид a b. Поэтому весь рассматриваемый фрагмент программы равносилен такому:
if not(a and b) then
P
else
R;
Однако его лучше (?!) переписать следующим образом:
if (a and b) then
R
else
P;
Упражнения: 1. Почему в программах лучше писать not(a and b), нежели not(a) or not(b), хотя по закону де Моргана эти операторы равносильны ?
2. Оптимизируйте фрагмент программы:
if (not(a or b and c) or not(b or c)) then
P
else
if (b and not(a and c)) then
Q
else
R;
3. Приведите ещё пару-тройку логических несуразностей из собственных программ.
Автоматизированный логический вывод формул. Пусть заданы формулы A1 , … , An , A от некоторого набора пропозициональных переменных и нужно понять, верно ли, что A1 , … , An
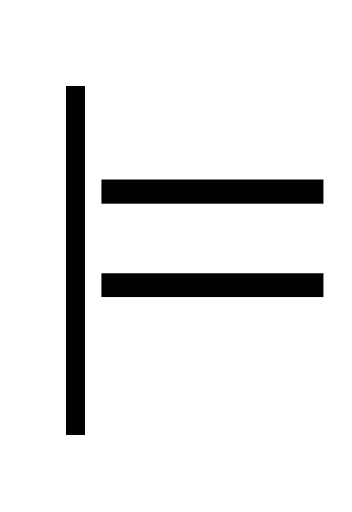A.
Оказывается, что для машинной проверки
удобно использовать правило
резолюций в
виде
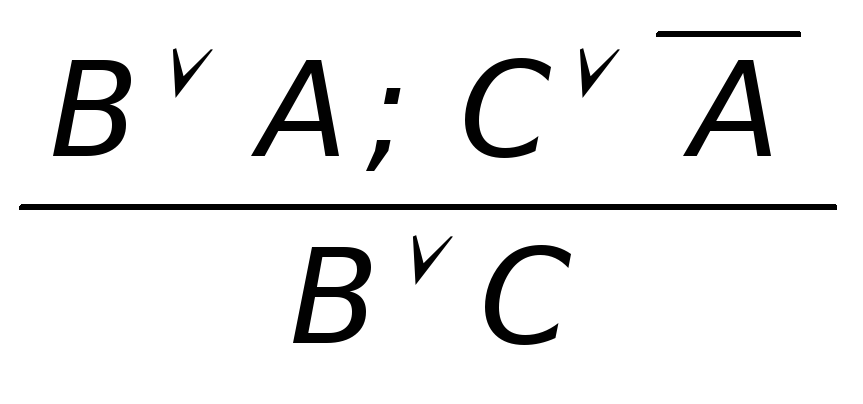или в терминах логического следованияA
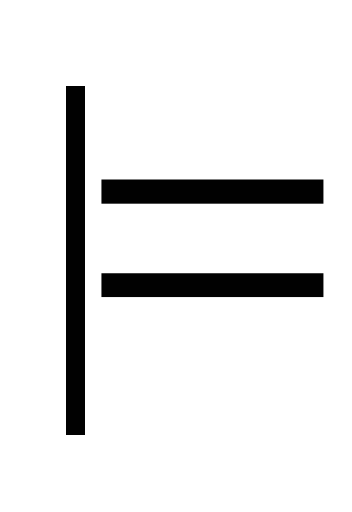B
,
C
B
C
.
Привычное человеку
правило modus
ponens
является
частным случаем этого правила резолюций
при B
0
: ввиду A
B
A
,
C
A
C
, B
C
C
правило
резолюций принимает знакомый вид
–modus
ponens.
Как было доказано,
логическое следование A1
, … , An
A
имеет место
тогда и только тогда, когда (A1
…
An
A)
1.
Удобнее перейти к отрицаниям:
0
.
Значит нужно
понять, что A1
…
An
0,
т.е. A1
…
An
Ф 
для некоторой
формулы Ф,
т.е. A1
, … , An
,
(этого
достаточно ?!).
Запишем посылки
A1
, … , An
,
в КНФ
и обозначим множество всех элементарных
дизъюнкций, участвующих в этих КНФ
через
= {D1
, … , Dm}.
Тогда каждая посылка, будучи конъюнкцией
некоторых элементов множества ,
является логическим следствием множества
формул
(по правилу
введения конъюнкции), т.е.
A1
, … ,
An
,
.
Поэтому
A1
…
An
и
Ф
.
Обратно, если
Ф
,
то D1
…
Dm
Ф
–закон
логики, причём D1
…
Dm
A1
…
An
,
т.к. каждая формула в правой части
является конъюнкцией некоторых
элементарных дизъюнкций из левой части,
а каждая дизъюнкция из левой части
встречается в одной из формул правой
части. Итак, задача о проверке следования
A1
, … , An
,
Ф
сводится к
проверке следования
Ф
для заданного
конечного множества
элементарных дизъюнкций.
Возникшую редуцированную задачу будем решать методом резолюций, который можно описать так:
перебираем
дизъюнкции из множества
, пока не
найдём пару вида
,
где
,
{0, 1, }
(1
s),
а запись
означает,
что переменная x
не участвует
в соответствующей дизъюнкции. Таким
образом, в Di
и Dj
переменная
xk
(для некоторого
k)
встречается
в одной дизъюнкции с отрицанием, а в
другой – без отрицания.
к этой паре применяем правило резолюций: если обозначить
,
то
, причём
, т.е.
дизъюнкция di
dj
будет логическим следствием формул
Di
, Dj
, а значит
и следствием множества
.
Возможен случай,
когда
, т.е.
дизъюнкции di
и dj
пустые.
Тогда очевидно, что
xk
,
т.е. можно взять Ф
= xk
.
Если же di
dj
1,
то рассматриваемое следствие тривиально
и такую резолюцию можно не делать. Так
будет, например, когда
=
{0, 1}. Таким
образом, можно ограничиться рассмотрением
дизъюнкций Di
и Dj
, в которых xk
– единственная переменная, встречающаяся
в одной из них с отрицанием, а в другой
– без отрицания.
Это ограничение
существенно сокращает перебор возможных
резолюций.
расширяем
множество
до
, присоединяя
к
все дизъюнкции
д1
, … , дm
из
КНФ
для di
dj
:
=
{д1
, … , дm},
di
dj
д1
…
дm
. Теперь
Ф
тогда и
только тогда, когда
Ф
.
Действительно, если противоречие Ф
следует из множества ,
то оно следует и из большего множества
.
Если же это противоречие следует из
множества ,
то оно следует и из
, т.к. каждый
элемент
является
логическим следствием множества
.
процесс построения резолюций можно ещё более сократить, если учесть, что
при появлении во
множестве
двух
дизъюнкций вида Д
и Д
D
можно оставить только одну из них –
более короткую Д,
т.к. Д
Д
D.
Описанный алгоритм
последовательного расширения множества
называется
замыканием
этого множества относительно резолюций.
На некотором
шаге ввиду конечности числа всех
дизъюнкций (от фиксированного конечного
числа переменных) либо получится вывод
искомого противоречия
xk
,
либо множество дизъюнкций, замкнутое
относительно резолюций,
т.е. такое
множество, которое описанный выше
процесс не расширяет: дизъюнкций Di
, Dj
описанного
выше вида в нём нет. В первом случае
получим A1
, … , An
A
для исходных
формул, а во втором формула A
не является
логическим следствием формул A1
, … , An
.
Примеры: 1. Проверить, следует ли формула A = y из
A1
= (x
y
)
(
y
z), A2
= (x
)
(
z)
.
Имеем
=
,
= {x
y
,
y
z, x
,
z,
}.
Из этого множества
сразу можно удалить все дизъюнкции,
строго содержащие
(они следуют из
).
Таким образом,
= { x
y
,
y
z,
}.
Процесс замыкания относительно резолюций таков:
x
y
,
x
,
и
= { x
y
,
y
z,
,
x
}.
Из этого множества
можно удалить все дизъюнкции, строго
содержащие x
,
т.е. оставить
= {
y
z,
,
x
}.
y
z,
z,
так что
= {
y
z,
,
x
,
z
} и после
удаления дизъюнкций, строго содержащих
z,
= {
,
x
,
z
}.
Других нетривиальных резолюций нет, замкнуто относительно резолюций, поэтому формула А не является логическим следствием формул A1 и A2 .
Этот результат можно, конечно, получить, построив таблицы истинности:
|
x |
y |
z |
x
y
|
|
|
x
|
A1 |
A2 |
A |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
y
z
z
2.
Верно ли, что (x
y
)
(
y
z),
x
y
z
y
?
Здесь
A
= y
,
A1
= (x
y
)
(
y
z), A2
= x
y
z
(y
z)
(
y)
(
z) .
При
этом
(x
z).
Поэтому
= { x
y
,
y
z
,
y,
z,
,
x
z
},
и после удаления
всех дизъюнкций, строго содержащих
z,
получим
= { x
y
,
y,
z,
,
x
z
}.
Теперь считаем нетривиальные резолюции:
x
y
,
y
(y
)
y
y
,
поэтому
= { x
y
,
y,
z,
,
x
z,
y
},
= {
y,
z,
,
x
z,
y
}.
y
,
,
и
= {
,
x
z,
y
,
}
.
,
y
,
т.е.
= {
,
x
z,
,
}.
x
z
,
z,
поэтому (4)
= {
,
,
,
z
}, и (4)
z
.
Итак, А1
, A2
A
. Проверьте
этот результат с помощью таблиц
истинности.
Изложенный алгоритм допускает программную реализацию, эффективность которой зависит от удобства организации представления данных в ЭВМ и порядка вычисления резолюций.
Проектирование, анализ и оптимизация релейно-контактных и больших интегральных схем. Рассмотрим лишь некоторые модельные задачи, иллюстрирующие методы этой важной и необъятной области современных технологий.
Задача 1. Разработать схему для предварительного отбора участников соревнований в следующий тур. Перед каждым из четырёх членов жюри находится выключатель, который включается, если этот член жюри считает участника достойным прохождения в следующий тур. На табло должна загораться лампочка, если большинством голосов, обязательно включая председателя, имеющего два голоса, жюри высказалось за прохождение участника в следующий тур.
Решение. Процесс проектирования проведём в несколько шагов:
1. Анализ логики задачи. Составим таблицу всех случаев, в которых должна загораться лампочка:
|
x1 |
x2 |
x3 |
x4 |
Л |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
2. Получение функции проводимости схемы. По таблице истинности напишем логическую функцию – функцию проводимости схемы:
Л(x1
, x2
, x3
, x4
) = (x1
x4
)
(x1
x3
)
(x1
x3
x4
)
(x1
x2
)
(x1
x2
x4
)
(x1
x2
x3
)
(x1
x2
x3
x4
).
3. Упрощение функции проводимости. Для того, чтобы схема получилась более компактной, эту функцию нужно упростить с помощью равносильных преобразований:
Л(x1
, x2
, x3
, x4
) = (x1
x4
)
(x1
x3
)
(x1
x3
x4
)
(x1
x2
)
(x1
x2
x4
)
(x1
x2
x3
)
(x1
x2
x3
x4
)
x1
[(
x4)
(
x3
)
(
x3
x4)
(x2
)
(x2
x4)
(x2
x3
)
(x2
x3
x4
)]
x1
[(
x4)
(
x3)
(x2
)
(x2
x3)]
x1
[(
x4)
x3
(x2
)]
x1
[(
x4)
(x2
x3)]
x1
[(
x4)
(x2
x3)]
x1 (x2 x3 x4 ).
Конечно, о таком результате в этой простейшей задаче можно было бы догадаться, внимательно прочитав условие. В случае сложных схем этапы генерации и упрощения логической функции можно автоматизировать.
4. Изображение схемы. Теперь можно нарисовать искомую релейно-контактную схему, используя следующие условные обозначения, позволяющие строить электрическую схему по логической функции:
|
Обозначения | |
|
логические |
релейно-контактные |
|
0 |
цепь разомкнута |
|
1 |
цепь замкнута |
|
|
инверсия |
|
x y |
последовательное соединение |
|
x y |
параллельное соединение |
Т
аким
образом, проектируемая схема выглядит
так:
З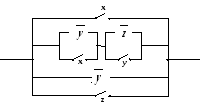
адача
2. Упростить
релейно-контактную схему, приведённую
ниже.
Учитывая реализацию последовательных и параллельных соединений в электрической схеме логическими связками конъюнкции и дизъюнкции соответственно, получаем функцию проводимости
f(x,
y,
z)
= x
[(
x)
(
y)]
z
.
После упрощения
f(x,
y,
z)
= x
[(
x)
(
y)]
z
x
[
x 
y
x
y]
z
x
(
)
(x 
)
(x
y)
z
(x
x 
x
y)
(
)
z
x
(1
y)
(
1)
z
x
z
р
исуем
новую схему:
Отличие электронных интегральных схем от обычных электрических состоит, во-первых, в том, что они позволяют использовать транзисторы, с помощью которых более просто и компактно проектируются стандартные электронные устройства (вентили), реализующие те или иные логические функции. Во-вторых, технология изготовления интегральных схем позволяет размещать на малой площади изготавливаемого кристалла большое количество элементов, обеспечивающих его многофункциональность.
С логической точки зрения процесс разработки интегральной схемы ничем не отличается от этапов построения электрической схемы: вначале выписывается булева функция проводимости, которая минимизируется и реализуется в схеме с использованием доступной элементной базы. Конечно, при этом необходимо ещё учесть технологические ограничения, которые, грубо говоря, не позволяют “лепить” слишком много элементов и “проводов” на ограниченном участке печатной платы. Эти ограничения здесь рассматриваться не будут, хотя и очень важны при реальном проектировании интегральных схем.
|
Обозначения | |
|
логические |
интегральных схем |
|
0 |
сигнал низкого уровня |
|
1 |
сигнал высокого уровня |
|
|
вентиль “НЕ” |
|
x y |
вентиль “И” |
|
x y |
вентиль “ИЛИ” |
Р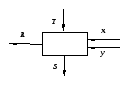
ассмотрим
пример проектированиясумматора
– реального
электронного устройства, складывающего
два n-разрядных
двоичных числа. При сложении чисел “в
столбик” цифры результата получаются
последовательно: справа налево. Для
получения очередной цифры нужно сложить
две текущие цифры слагаемых и учесть
полученный на предыдущем шаге перенос.
Таким образом, сумматор можно проектировать
на основе
конвейерной технологии,
часто используемой при создании
разнообразных сложных интегральных
схем. Именно, достаточно создать более
простое устройство –
одноразрядный сумматор:
п
олучающий
на входах очередные суммируемые цифрыx,
y
а также бит
переноса T,
и дающий на выходах очередную цифру
результата R
и новый бит
переноса S.
Если такое устройство создано, то
n-разрядный
сумматор можно построить в соответствии
со следующей схемой. Здесь начальный
бит переноса S–1
равен 0,
и вырабатываемые в дальнейшем биты
переноса передаются “по конвейеру”.
Последний бит переноса Sn–1
даёт
информацию о переполнении:
он равен единице в том и только том
случае, если результат сложения не
помещается в n
разрядов.
|
x |
y |
T |
S |
R |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
S(x, y,
T) = (x
y 
)
(x 
T)
(
y
T)
(x
y
T),
R(x, y,
T) = (x 
)
(
y 
)
(
T)
(x
y
T).
Теперь эти функции нужно упростить. Оказывается,
S(x, y, T) (x y) (x T) (y T),
R(x, y,
T)
(x
y
T)
(x
y
T),
что следует из таблицы истинности правых частей r и s этих равенств.
|
x |
y |
T |
R |
S |
|
x y T |
x y T |
r |
x y |
x T |
y T |
s |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Т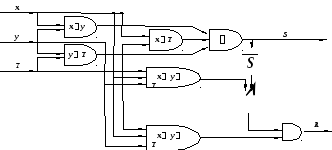
аким
образом, можно построить следующую
схему одноразрядного сумматора, где
вентили конъюнкции и дизъюнкции трёх
величин можно получить, два раза выполнив
соответствующие операции с двумя
аргументами.