§ 3. Истинностные значения формул

Истинность или ложность элементарных высказываний оставляется на совести той области знания, к которой они относятся. Логика позволяет по заданным истинностным значениям элементарных высказываний вычислять истинностные значения построенных из них сложных высказываний.

Прежде, чем переходить к формальным рассуждениям, введём следующие соглашения: вместо значения истина будем писать 1, а вместо значения ложь – 0. Интерпретацией формулы A(x₁ , … , x_n) назовём любой набор  = (₁ ; … ; _n) значений переменных x₁ = ₁ , … , x_n = _n (_i  {0, 1}, 1  i  n).

Теперь любой формуле исчисления высказываний A(x₁ , … , x_n) от пропозициональных переменных x₁ , … , x_n можно присвоить истинностное значение A() = A(₁ , … , _n )  {0, 1} при данной интерпретации  = (₁ ; … ; _n) по следующим правилам:

(И1): если A(x₁ , … , x_n) – одна из пропозициональных переменных x₁ , … , x_n , то её истинностное значение уже определено: в случае A(x₁ , … , x_n) = x_i полагаем A() = _i ;

(И2): если A(x₁ , … , x_n) = (B(x₁ , … , x_n)  C(x₁ , … , x_n)) или A(x₁ , … , x_n) = = , где – одна из логических связок  ,  ,  ,  (т.е. формула A(x₁ , … , x_n) получена из более простых формул B(x₁ , … , x_n) и C(x₁ , … , x_n) с помощью одной из конструкций правила образования формул (Ф2)), а значения B() = B(₁ , … , _n ) и C() = С(₁ , … , _n ) уже вычислены, то истинностное значение A() = A(₁ , … , _n ) приписывается с помощью следующих аксиом логических связок:

B()	C()	()	(B()  C())	(B()  C())	(B()  C())	(B()  C())
0	0	1	0	0	1	1
0	1	1	0	1	1	0
1	0	0	0	1	0	0
1	1	0	1	1	1	1

Следует подчеркнуть, что законы вычисления этих логических связок являются именно аксиомами – они принимаются на веру. Часть из них согласуется со здравым смыслом и интуитивными описаниями значения логических связок. Некоторые значения менее очевидны, и осознание необходимости их использования нуждается в дополнительных аргументах, которые рождаются только в результате работы мысли.

Наиболее трудна для понимания аксиома вычисления импликации, в частности, нуждается в дополнительных аргументах тот факт, что при ложной посылке B() значение импликации всегда истинно. По смыслу логическая связка импликация  означает следование, выводимость. Таким образом, нужно понять, почему из ложного утверждения выводится любое другое. В связи с этим невозможно не упомянуть случай, произошедший с Бертраном Расселом – известным специалистом по математической логике XX в. Он читал лекцию для философов, когда один из них попросил объяснить, почему из ложного утверждения можно вывести всё, что угодно ? Тогда Рассел для примера доказал, что из утверждения 22 = 5 следует, что он – Папа Римский. Вот это остроумное доказательство:

22 = 5, 2+2 = 2+3, 2 = 3, 1+1 = 2+1, 1 = 2,

Рассел и Папа Римский – их двое, но 2 = 1, так что они – одно лицо, ч.т.д.

Отметим ещё, что значение импликации огромно: любое научное утверждение формулируется в импликативном виде, т.е. в виде импликации A  B. Например, теорема Пифагора “сумма квадратов катетов равна квадрату гипотенузы” на самом деле означает следующее: если ABC – треугольник с прямым углом C, то AB² = AC² + BC². Точно так же формулируются и утверждения других наук: в них всегда должна присутствовать посылка А и заключение В, а само утверждение означает истинность импликации A  B. Если посылка А истинна, то истинность импликации означает истинность заключения В. Если же посылка ложна, то импликация всё равно истинна. Поэтому, если вдруг выяснилось, что В ложно, это ещё не значит, что нарушен закон той или иной науки, просто, возможно, посылка А стала ложной, а импликация всё равно истинна.

Как с помощью сформулированных аксиом вычислить значение любой формулы при заданных значениях её пропозициональных переменных ? Значение формулы вычисляется последовательно, начиная со значений пропозициональных переменных в соответствии с построением самой формулы по правилу (Ф2) с применением на каждом шаге описанных выше аксиом.

Примеры: 1. Вычислить значение формулы ( b) при a = 1, b = 0.

Формула ( b) построена из формул и b путём применением конструкции (A  B) правила (Ф2). Поэтому вначале нужно вычислить значения формул и b, а затем применить аксиому вычисления дизъюнкции. Значение b = 0 дано, а значение формулы вычисляется из заданного значения формулы a по аксиоме значения отрицания: = 0. Таким образом, по аксиоме значения дизъюнкции получаем в итоге ( b) = (0  0) = 0.

Следует отметить, что при других наборах значений переменных значение этой же формулы может быть другим. Например, если a = 0 = b, то = 1и ( b) = (1  0) = 1.

2. Вычислить значение формулы ( c) при a = 1, b = 1, c = 0 .

Опишем процесс построения формулы по правилу (Ф2), одновременно вычисляя на каждом шаге истинностные значения получаемых формул при заданных значениях пропозициональных переменных: a = 1, b = 1, c = 0, (a  b) = 1, = 0, (  c) = (0  0) = 1. Таким образом, искомое значение равно 1.

Для a = 0, b = 0, с = 0 получим (a  b) = (0  0) = 0, = 1, ( c) = (1 0) = 0.

Предыдущие примеры показывают, что значение формулы зависит от конкретного набора её пропозициональных переменных, т.е. от конкретной интерпретации формулы: при разных интерпретациях значения формулы могут быть различными. Поэтому говорить об истинности или ложности формулы, не указывая интерпретации, бессмысленно.

x1	…	xn	…	A(x1 , … , xn )
…	…	…	…	…
1	…	n	…	A(1 , … , n )
…	…	…	…	…

На практике обычно заранее неизвестно, какие именно значения принимают пропозициональные переменные. Поэтому для нахождения всех истинностных значений формулы A(x₁ , … , x_n ) строят её таблицу истинности, т.е. таблицу указанного слева вида, которая имеет (как будет показано ниже) 2ⁿ строк, каждая из которых в первых n столбцах содержит конкретные значения ₁ , … , _n пропозициональных переменных x₁ , … , x_n , в последующих столбцах – вычисленные промежуточные значения более простых формул, из которых строится рассматриваемая формула, а в последнем столбце – значение формулы A(x₁ , … , x_n ) при интерпретации  = (₁ ; … ; _n) . При этом в первых n столбцах таблицы истинности должны быть ровно по одному разу перечислены все возможные наборы значений пропозицииональных переменных x₁ , … , x_n .

Примеры: 1. Строим таблицы истинности формул  b и .

a	b					b						a			b		a  b						b  a				
0	0		1			1						0			0		1				0		1		0		0
0	1		1			1						0			1		1				0		0		1		0
1	0		0			0						1			0		0				1		1		0		0
1	1		0			1						1			1		1				0		1		0		0

a	b	c	1	2	3	4	5	6
0	0	0	0	0	0	0	0	1
0	0	1	0	1	1	1	1	1
0	1	0	0	0	0	1	0	1
0	1	1	0	1	1	1	1	1
1	0	0	0	0	1	0	0	1
1	0	1	0	1	1	1	1	1
1	1	0	1	1	1	1	1	1
1	1	1	1	1	1	1	1	1

2. Построим таблицу истинности для формулы ((a  b)  c)  ((a  c)  (b  c)).

В ней цифрами обозначены формулы: 1 = (a  b), 2 = (1  c), 3 = (a  c), 4 = (b  c), 5 = (3  4), 6 = 2  5. Такие сокращения удобны для построения таблиц истинности громоздких формул. Использованные в обозначениях числа определяют и порядок вычислений.

Для того чтобы успешно строить таблицы истинности формул, нужно иметь алгоритм перечисления всех возможных наборов значений n её пропозициональных переменных x₁ , … , x_n . Можно воспользоваться, например, двоичной системой счисления: каждая интерпретация  = (₁ ; … ; _n ) отождествляется с двоичным числом изn двоичных цифр ₁ , … , _n  {0, 1}, которое в десятичном виде выглядит как ₁2^n–1 + … + _n2⁰. Наименьшее число 0 = 0 … 0₂ = = 02^n–1+…+02⁰ соответствует интерпретации  = (0 ; … ; 0 ), а наибольшее 1 … 1₂ = 12^n–1+…+12⁰ = 2^n–1+2^n–2+…+2+1 = = 2ⁿ – 1 (по формуле суммирования геометрической прогрессии) – интерпретации  = (1 ; … ; 1). Поэтому для перечисления всех интер­претаций достаточно исполь­зовать двоичные

0	2	10	2	10	2	10	2
0	00000	8	01000	16	10000	24	11000
1	00001	9	01001	17	10001	25	11001
2	00010	10	01010	18	10010	26	11010
3	00011	11	01011	19	10011	27	11011
4	00100	12	01100	20	10100	28	11100
5	00101	13	01101	21	10101	29	11101
6	00110	14	01110	22	10110	30	11110
7	00111	15	01111	23	10111	31	11111

коды чисел от 0 до 2ⁿ – 1, которые приве­дены в таблице (n = 5).

Здесь использована пя­тиразрядная двоичная запись чисел, но незначащие нули по мере необходимости можно отбросить так же, как это сделано в приводимых ниже примерах перечисления интерпретаций для n = 1, 2, 3, 4.

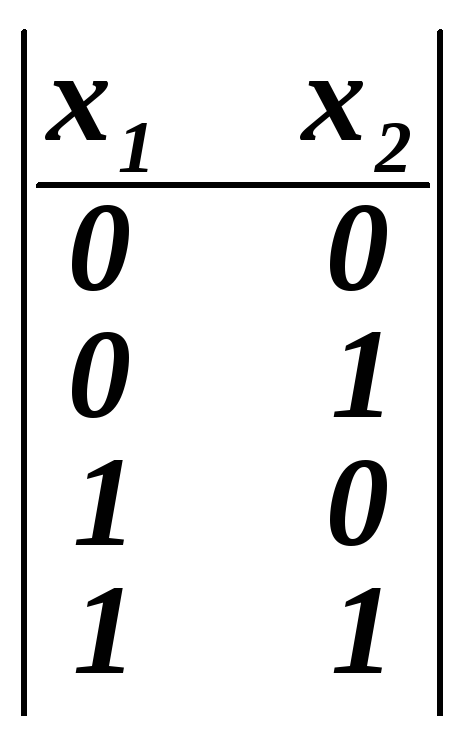Примеры: n = 1: ,n =2: ,n = 3: ,n = 4:

Теорема (о правиле перечисления интерпретаций). В таблице, построенной путём выписывания n-значных двоичных кодов всех чисел от 0 до 2ⁿ – 1, перечисляются ровно по одному разу всевозможные наборы значений n пропозициональных переменных.

Доказательство. Как было отмечено, каждой интерпретации  = (₁ ; … ; _n ) соответствует двоичное число изn двоичных цифр ₁ , … , _n , которое находится в диапазоне от 0 до 2ⁿ – 1. При этом разным интерпретациям будут отвечать и разные числа: если  = (₁ ; … ; _n )  (₁ ; … ; _n) = , то . Кроме того, в результате такого сопоставления будут перечислены без пропусковвсе двоичные числа от 0 до 2ⁿ – 1 : число появится при рассмотрении интерпретации = (₁ ; … ; _n ).

Теорема доказана.

Следствие (о количестве наборов из нулей и единиц длины n). Количество всевозможных наборов длины n из нулей и единиц равно 2ⁿ . Столько же и строк в любой таблице истинности формулы от n переменных.

Доказательство очевидно, т.к. количество всевозможных наборов длины n из нулей и единиц равно количеству всевозможных интерпретаций для n пропозициональных переменных, которое (ввиду доказанной теоремы) равно количеству чисел от 0 до 2ⁿ – 1, т.е. 2ⁿ. Следствие доказано.

Следствие (о количестве подмножеств n-элементного множества). Любое n-эле­ментное множество содержит 2ⁿ подмножеств.

Доказательство. Пусть дано множество A = {a₁ , … , a_n }. Каждому его подмножеству X  A сопоставим набор (₁ ; … ; _n ) из нулей и единиц длины n, полностью определяющий это подмножество. Для этого положим _i = 1, если a_i  X, и _i = 0, если a_i  X (1  i  n). Кстати, именно такой способ интерпретации множеств реализуется в некоторых языках программирования.

Примеры: Для множества A = {a₁ , a₂ , a₃ } подмножеству Х = {a₁ , a₃} будет соответствовать набор (1; 0; 1), а подмножеству Х = {a₂ } – набор (0; 1; 0). Пустому подмножеству (не содержащему элементов) будет сопоставлен набор (0; 0; 0), а всему множеству А – набор (1; 1; 1).

Легко понять, что по любому набору (₁ ; … ; _n ) из нулей и единиц длины n однозначно восстанавливается соответствующее ему подмножество: именно в множестве X нужно собрать все те элементы a_i , для которых _i = 1 (1  i  n). Поэтому подмножеств в n-элементном множестве будет столько, сколько существует наборов из нулей и единиц длины n, т.е. 2ⁿ. Следствие доказано.

Пример. Перечислим все подмножества 4-элементного множества.

Будем перечислять подмножества, выписывая соответствующие им наборы нулей и единиц, построенные по двоичным числам из диапазона от 0 до 2⁴ = 16:

№	набор	подмножество	№	набор	подмножество
0	(0; 0; 0; 0)		8	(1; 0; 0; 0)	{a1 }
1	(0; 0; 0; 1)	{a4 }	9	(1; 0; 0; 1)	{a1 , a4 }
2	(0; 0; 1; 0)	{a3 }	10	(1; 0; 1; 0)	{a1 , a3 }
3	(0; 0; 1; 1)	{a3 , a4 }	11	(1; 0; 1; 1)	{a1 , a3 , a4 }
4	(0; 1; 0; 0)	{a2 }	12	(1; 1; 0; 0)	{a1 , a2 }
5	(0; 1; 0; 1)	{a2 , a4 }	13	(1; 1; 0; 1)	{a1 , a2 , a4 }
6	(0; 1; 1; 0)	{a2 , a3 }	14	(1; 1; 1; 0)	{a1 , a2 , a3 }
7	(0; 1; 1; 1)	{a2 , a3 , a4 }	15	(1; 1; 1; 1)	{a1 , a2 , a3 , a4 }