История возникновения и развития комбинаторики

Ориентация на общее развитие личности в процессе образования включает элементы истории математики. Использование историко-математического материала на занятиях содействует повышению их общей эффективности. Математика предстает перед студентами не сформировавшейся наукой, а в процессе создания, в динамике. История науки позволяет учащимся увидеть ее движущие силы, наблюдать в действии взаимосвязь и взаимообусловленность научного познания и практической деятельности человека. «Лучший метод для предвидения будущего развития математических наук заключается в изучении истории и нынешнего состояния этих наук» отмечал А.Пуанкаре³.

С этой точки зрения, целесообразно начинать изучение комбинаторики с истории возникновения и развития данной науки.

Прежде, чем та или иная область знания сформируется в особую науку, она проходит длительный период накопления эмпирического материала, период развития в недрах другой, более общей науки, и затем выделяется в самостоятельную науку. Не является исключением и наука про общие законы комбинирования и образования различных конфигураций объектов, получившая название «комбинаторика». Еще в доисторическую эпоху люди столкнулись с проблемой выбора тех или иных объектов, расположения их в определенном порядке, нахождения среди различных расположений подходящих. Например, во время охоты необходимо было выбрать наилучшее расположение охотников, во время битвы – расположение воинов. Они находили свое применение и в часы досуга. «Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие умения рассчитывать, составлять планы и опровергать планы противника. О таких играх английский поэт У. Вордсворт писал:

«Не нужно нам владеть клинком.

Не ищем славы громкой.

Тот побеждает, кто знаком

С искусством мыслить тонким»⁴

Среди вещей египетского фараона Тутанхамона, который был захоронен 35 веков назад, в пирамиде, были найдены разграфленные доски, с 3 горизонталями и 10 вертикалями, и фигурки для древней игры «сенет». Ее правила не дошли до наших дней.

В дальнейшем в таких играх, как нарды, шахматы и различных их вариантах (китайские и японские шахматы, японские шашки «го» и т.д.), необходимо было рассматривать различные сочетания передвигаемых фигур. И, как правило, выигрывал тот, кто лучше решал задачи по наиболее удачному расположению фигур.

Вопросы, связанные с комбинаторикой, встречаются в китайских рукописях, относящихся к XIII XII вв. до н.э.⁵ Китайцы считали, что «все в мире является сочетанием двух начал – мужского и женского, которые обозначались символами ― и −−.». В рукописи «Же Ким» («Книга перестановок») показаны различные соединения этих знаков по два и по три.

— — —	−− — —	— −− —	−− −− —	— — −−	−− — −−	— −− −−	−− −− −−
k’ien небо	tui пар	li огонь	chon гром	sűn dtnth	k’an djlf	kön гора	k’un земля
7	6	5	4	3	2	1	0
Юг	Юго-Восток	Восток	Северо-Восток	Юго-Запад	Запад	Северо-Запад	Север

«Восемь рисунков из трех рядов символов изображали землю, горы, воду, ветер, грозу, огонь, облака и небо (некоторые рисунки имели и иные значения)». Неудивительно поэтому, что сумма первых 8 натуральных чисел воплощала в представлениях древних китайцев весь мир. Позже были составлены 64 фигуры, содержавшие пять рядов черточек. Видимо, автор рукописи «Же Ким» заметил удвоение числа рисунков при добавлении одного ряда символов. Это можно рассматривать как первый общий результат комбинаторики⁶.

Из рукописи «Же Ким» мы можем также узнать, что император Ию, который жил примерно 4000 лет назад, «нашел на берегу реки священную черепаху, на ее панцире был изображен рисунок из черных и белых кружков».

Рис. 1

Если заменить каждую фигурку соответствующим числом, возникнет такая таблица:

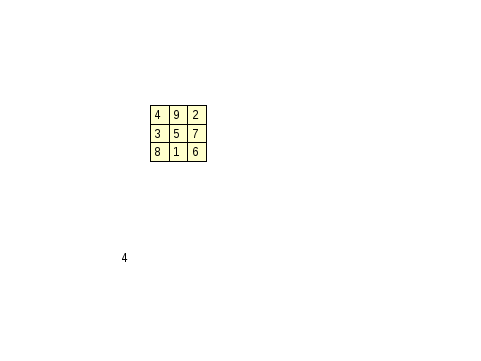Рис.2

Если сложить числа в каждой строке, столбце и диагонали, то получится одна и та же сумма 15. В древности китайцы давали мистическое толкование числам. Когда китайцы открыли таблицу с такими чудесными свойствами, то она произвела на них неизгладимое впечатление. Данный рисунок назвали «ло-шу», стали употреблять его при заклинаниях и считать магическим символом. «Магическим квадратом» теперь называют любую квадратную таблицу с одинаковыми суммами по каждой строке, столбце и диагонали.

Комбинаторные задачи, касавшиеся перечисления небольших групп предметов, решали греки. Аристотель описал без пропусков все виды правильных трехчленных силлогизмов, а его ученик Арисксен из Тарента перечислил различные комбинации длинных и коротких слогов в стихотворных размерах. Живший в IV в. н.э. математик Папп рассматривал число пар и троек, которые можно получить из трех элементов, допуская их повторения.

В XVIII веке происходит расцвет арабской науки. Арабами были переведены многие работы греческих и римских ученых. Арабские алгебраисты, при извлечении корней, вывели формулу для степени суммы двух чисел, которая в истории математики известна нам под названием «бином Ньютона». Историки считают, что эту формулу знал поэт и математик Омар Хайам (XI–XII вв.) Ее в XIII веке приводит в своих трудах Насир ад-Динат-Туси, а в XV веке она была исследована Джемшид ибн Масуд аль-Каши.

Как сообщают нам некоторые европейские источники, восходящие к арабским оригиналам, «коэффициенты этой формулы высчитывали следующим образом: брали число 10001 и возводили его во вторую, третью, четвертую, …, девятую степени»⁷. Составлялась таблица, имеющая следующий вид:

1000900360084012601260084003600090001 100080028005600700056002800080001 10007002100350035002100070001 1000600150020001500060001 100050010001000050001 10004000600040001 1000300030001 100020001 10001

При опускании в таблице лишних нулей получается треугольная таблица из биномиальных коэффициентов. Арабские ученые знали и основное свойство элементов этой таблицы, выражающееся формулой .

В вычислении биномиальных коэффициентов не отставали от арабов и китайские математики. Уже к XIII веку в книге алгебраиста Чжу Ши-дза «Яшмовое зеркало» приводится таблица таких чисел, вплоть до n=8. Известно также, что «в VIII веке астроном И.Синь вычислил количество различных расположений фигур в игре, которая напоминала шахматы».

Интерес к сочетаниям проявлялся и в Индии. В VII веке индийский математик Бхаскара в книге «Лилавати», изучая проблемы комбинаторики, писал о применении перестановок к подсчету вариаций размера в стихосложении, различных расположений в архитектуре и т. п. В его работе мы можем найти правила для отыскания числа перестановок и сочетаний нескольких предметов. При этом им также рассматривается и случай, когда в перестановках есть повторяющиеся элементы.

В результате развития торговли с Востоком в начале XII века арабская наука проникает в Западную Европу. В то время арабское учебное заведение окончил Леонардо – сын пизанского купца, торговавшего в Алжире. «Он написал книгу «Liber Abaci», которая вышла 1202 году. Леонардо получил прозвище Фибоначчи, он привел в систему всю арифметику арабов», некоторые сведения по геометрии Евклида и добавил к ним результаты своих изысканий. В работе Фибоначчи излагаются новые комбинаторные задачи, например, «об отыскании наименьшего количества гирь, с помощью которых можно получить любой целый вес от 1 до 40 фунтов»⁸. Леонардо уделял внимание и отысканию целых решений уравнений. Рассмотрение аналогичных задач в последствии привело к появлению количества натуральных решений систем уравнений и неравенств, имеющих право на рассмотрение как на одну из глав комбинаторики. Леонардо выявил новую последовательность, наряду с известными еще со времен греческих математиков, арифметической и геометрической прогрессий, каждый член которых получался по определенным правилам из предыдущих, члены новой последовательности были связаны друг с другом соотношением . Это было первой формулой, где каждый следующий член последовательности выражался через два предыдущих. Подобные формулы получили название рекуррентных (от лат.recurrere – возвращаться). Метод рекуррентных формул оказался впоследствии полезен для решения комбинаторных задач.

Существовавшие еще в глубокой древности азартные игры, получившие особенное распространение после крестовых походов, способствовали развитию комбинаторики.

Наибольшее распространение получила игра в кости – два или три кубика с нанесенными на них очками бросали на стол, и ставку брал тот, у кого выпала большая сумма очков. Несмотря на грозные запреты церкви, азартные игры все же развивались. В любом городе можно было наблюдать картину, которая описана в «Божественной комедии» Данте:

Когда кончается игра в три кости, То проигравший снова их берет, И мечет их один в унылой злости; Другого провожает весь народ…

В кости играли еще этруски жители Мохенджо-Даро, это известно из археологических раскопок. Однако, эти древние игры не подвергались математическому исследованию довольно долго.

Позже некоторые игроки, которые наиболее часто играли в кости, подметили, что одни суммы очков выпадают часто, а другие – редко. Были составлены таблицы, показывавшие, сколькими способами можно получить то или иное число очков. Сначала допускалась ошибка – подсчитывали только число различных сочетаний, дававших данную сумму.

Например, при бросании двух костей сумма 6 получается из сочетаний (1, 5), (2, 4), (3, 3), а сумма 7 – из сочетаний (1, 0), (2, 5), (3, 4). Так как три сочетания были различны в обоих случаях, то напрашивался ошибочный вывод о том, что суммы очков 6, 7 и 8 (также получаемая из трех сочетаний костей) должны выпадать одинаково часто. Но согласно опыту 7 очков выпадает чаще. Сочетание (3, 3) при бросании двух костей может быть получено единственным способом, а сочетание (3, 4) – двумя способами. Именно благодаря этому, сумма 7 выпадает наиболее часто. Таким образом, оказалось, что надо учитывать не только сочетание очков, но и их порядок.

Этими вопросами занимались такие известные итальянские математики XVI века, как Д. Кардано, Н. Тарталья и др. Наиболее полно исследовал данный вопрос в XVII веке Галилео Галилей, но его рукопись оставалась неопубликованной до 1718 г.

В 1713 г. была опубликована книга «Искусство предположений» Якоба Бернулли, в которой указывались формулы для числа размещений из элементов по, выводились выражения для степенных сумм и т. д.

Работы Б.Паскаля⁹ и П.Ферма¹⁰ ознаменовали рождение двух новых ветвей математической науки – комбинаторики и теории вероятностей. Ранее комбинаторные проблемы лишь затрагивались в общих трудах по астрологии, логике и математике или большей частью относились к области математических развлечений. В 1666 году В. Лейбниц¹¹ публикует «Диссертацию о комбинаторном искусстве», в которой впервые появляется термин «комбинаторный». Этот математический труд Лейбница должен был стать лишь началом большой работы, о которой он часто упоминал в своих письмах и печатных трудах. В. Лейбниц планировал для комбинаторики многочисленные приложения: к играм, статистике, к кодированию и декодированию, к теории наблюдений. Он считал, что комбинаторика должна заниматься «одинаковым и различным, похожим и непохожим, абсолютным и относительным расположением, в то время как обычная математика занимается большим и малым, единицей и многим, целым и частью». Иными словами, под комбинаторикой В. Лейбниц понимал примерно то, что мы теперь называем дискретной математикой. К области комбинаторики В. Лейбниц относил и «универсальную характеристику» – математику суждений, то есть прообраз нынешней математической логики. Проекты В. Лейбница казались несбыточными математикам его времени, но сейчас, после создания быстродействующих вычислительных устройств, многие его планы стали претворяться в жизнь, а дискретная математика выросла в своем значении и начала соперничать с математическим анализом.

Замечательные достижения в области комбинаторики принадлежат одному из величайших математиков XVIII века Леонарду Эйлеру¹², швейцарцу, прожившему почти всю жизнь в России, где он был членом Петербургской академии наук.

Основная часть научной работы Л. Эйлера посвящена математическому анализу, в котором он проложил новые пути, создал целый ряд новых областей и подвел итоги исследованиям в других областях. Но у Л. Эйлера хватало времени размышлять и над задачами, которые, казалось бы, не заслуживали его внимания,– о том, можно ли обойти мосты в Кенигсберге (ныне Калининграде) так, чтобы не побывать дважды на одном и том же мосту? – можно ли поставить 36 офицеров из 6 разных полков так, чтобы в каждой шеренге и каждой колонне было по одному офицеру каждого воинского звания из каждого полка? – сколькими способами можно разбить данное число на слагаемые и т.д. Работа о мостах явилась зерном, из которого впоследствии выросли топология и теория графов, задача об офицерах оказалась сейчас связанной с планированием экспериментов, а методы, использованные при решении задачи о разбиении чисел, после длительного и сложного пути развития превратились в науку об интегральных преобразованиях, применяемую для решения уравнений математической физики.

После работ Б.Паскаля и П.Ферма, Г.Лейбница и Л.Эйлера можно было уже говорить о комбинаторике как о самостоятельном разделе математики, тесно связанном с другими областями науки, такими, как теория вероятностей, учение о рядах и т.д. Таким образом, комбинаторика как самостоятельная ветвь математики возникла в XVII веке.

На протяжении долгого времени основную роль в изучении мироздания играл математический анализ – дифференциальное и интегральное исчисления, дифференциальные уравнения, уравнения математической физики, вариационное исчисление и т.д. Все процессы рассматривались как непрерывные, чтобы можно было применять к ним развитый аппарат математики непрерывного. С появлением быстродействующих вычислительных машин такие абстрактные области математики, как математическая логика, общая алгебра, стали прикладными. Тогда для составления алгоритмических языков, на которых стали писать программы для машин, понадобились специалисты именно в этих областях математики. Произошло изменение соотношения между дискретной и классической математикой.

Изменилась и роль древнейшей области дискретной математики – комбинаторики. Если раньше комбинаторика применялась для составления занимательных задач, для кодирования и расшифровки древних письменностей, то со временем она превращается в важнейшую область математического знания.