Глава II Графы и сети

Многие задачи дискретной оптимизации могут быть интерпретированы как задачи на сетях и графах. В этой главе мы введем основные понятия теории графов и рассмотрим способы представления сетей и графов в ЭВМ.

§1. Графы, сети

Под неориентированным графом (или короче графим) будем понимать произвольную пару G = (V,E) конечных множеств V и Е таких, что Е {{v,w} : v,w V, v ≠ w}. Здесь и далее запись {v,w} обозначает неупорядоченную пару элементов v и w.

Элементы множества V будем называть вершинами графа G. а элементы Е — ребрами графа G. Если е = {v,w} — ребро графа, то вершины v и w будем называть концами ребра е, а ребро е — инцидентным вершинам v и w. Две вершины графа v и w назы­ваются смежными, если есть ребро в графе, их соединяющее, т.е. {v,w}Е.

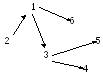Ориентированным графом (или короче орграфом) будем называть произвольную пару G = (V, E) конечных множеств V и E такую, что Е {(v,w) : v,w V,v≠w}VV. Здесь и далее запись (v,w) обозначает упорядоченную пару элементов v и w. Говоря об орграфе, элементы множества V будем называть узлами орграфа, а элементы Е дугами Если е = (v,w) — дуга орграфа, то будем говорить, что v начало дуги е, w — конец дуги е, и. что дуга е исходит из узла v и входит в узел w.

6

а)

б)

Рис. 2.1. Изображение графов и орграфов, а) Неориентированный граф, б) Ориентированный гриф

Графы и орграфы обычно изображаются на плоскости и им и множества точек, соответствующих вершинам или узлам, и множества линий, соединяющих эти точки, которые соответствуют ребрам или дугам. Линия, изображающая ребро {v,w} или дугу (v,w), соединяет точки, изображающие вершины v и w, причем в случае ориентированного графа эта линия снабжается стрелкой, обозначающей направление от v к w. Удобно вершины графа считать пронумерованными натуральными числами, и на рисунках сразу вместо точки ставить соответствующий номер

Число ребер, инцидентных данной вершине, называется степенью вершины. Вершины степени 1 называют висячими вершинами, а степени 0 — изолированными. Например, в графе, изображенном на рис. 2.1.а, вершины 2, 5, 6 являются висячими и вершина 7 — изолированной.

Степенью захода узла в некотором орграфе называется число дуг, в нее входящих, степенью исхода — из нее исходящих. Под степенью узла будем понимать сумму степеней исхода и захода данного узла. Например, в орграфе, изображенном на рис. 2.1.б, степень исхода узла 1 равна 2, а степень захода — 1.

Цепью (соответственно путем) в графе (орграфе) G = (V,E) назовем чередующуюся последовательность вершин и ребер (узлов и дуг) v₀,e₀,V₁, ... ,e_k-1, v_k такую, что каждое ребро e_k соединяет вершины v_k и v_k+1 (соответственно исходит из v_k и входит в v_k+1). Вершины (узлы) v₀ и v_k будем называть соответственно началом и концом цепи (пути). Если все вершины (узлы) цепи (пути) различны, то такую цепь (путь) будем называть простои цепью (простым путем).

Цепь в графе (соответственно путь), начальная и конечная вершины (узлы) которого совпадают, будем называть циклом {контуром). Если в цикле (соответственно в контуре) все проме­жуточные вершины различны, то такой цикл (контур) будем на­зывать простым.

Иногда нам будет удобно цепь (путь) v₀,e₀,v₁, ... , e_k-1,v_k отожде­ствлять с множеством ребер (дуг) е₀, ... , e_k-1 или вершин (узлов) v₀,v₁, ... ,v_k, ее (его) образующих. Длиной цепи (пути) будем назы­вать число входящих в нее ребер (дуг).

Подграфом графа (орграфа) G = (V,E) будем называть произ­вольный граф (орграф) G' = (V',E') такой, что V' Vи Е'Е.

Пусть G=(V,E) — произвольный неориентированный граф и пусть vV. Пусть V' — множество тех вершин wV, к которым существует цепь из вершины v. Множество V' вместе с ребрами графа G, инцидентными вершинам из V', определяет некоторый подграф графа G, называемый связной компонентой графа G, содержащей данную вершину v.

Легко доказать, что множества вершин различных компонент связности произвольного графа попарно не пересекаются. На­пример, для графа, изображенного на рис. 2.1.а, это множества V₁, = {1,2,3,4}, V₂ = {5,6}, V₃,= {7}.

Граф, имеющий ровно одну компоненту связности, будем на­зывать связным. Непосредственно из определения вытекает

Предложение 2.1. Неориентированный граф G=(V,E) связен тогда и только тогда, когда для любых вершин v,wV существу­ет цепь в графе G, их соединяющая.

Для орграфа G (V.E) через G*=(V*,E*) обозначим неориенти­рованный граф, для которого V*=V и {v,w} Е* тогда и только тогда, когда либо (v,w) E, либо (w,v) Е. Иначе говоря, граф G* получается из орграфа G уничтожением ориентации дуг. Орг­раф G будем называть связным, если соответствующий граф G* связен.

Всюду в дальнейшем через |А| будем обозначать количество элементов конечного множества А. Говоря о некотором графе или орграфе G=(V,E), через n будем обозначать количество вер­шин (или узлов), а через m — количество ребер (или дуг), то есть будем полагать n=|V|, m=|E|.

Поскольку мы условились считать, что в графах и орграфах нет ребер вида {v,v} и дуг вида (v,v) (так называемых петель), и, что для любых v,wV существует не более одного ребра или не более двух дуг им инцидентных, то справедливы неравенства:

1. m ≤ n∙(n-1 )/2 — для неориентированных графов,

2. m ≤ n∙(n-l) — для орграфов.

Одним из важнейших понятий в теории графов является поня­тие дерева. Деревом называется связный неориентированный граф без циклов. Следующая теорема будет часто использовать­ся

Теорема 2.1. Пусть G = (V,E) — граф, n=|V|, m=|E|. Тогда сле­дующие условия эквивалентны:

1. G — дерево.

2. Для любых двух вершин u,v е V существует и притом единственная цепь, их соединяющая.

3. Граф G связен, и m=n-l.

4. Граф G не содержит циклов, и m=n-l.

5. Граф G не содержит циклов, и при соединении любых двух несмежных вершин ребром образуется ровно один цикл.

□ 1.2. Ясно, что если между некоторыми вершинами u иv имеется две цепи, то граф содержит цикл.

2. 3. Пусть v₀,v₁, ... ,v_k — максимальная по включению цепь в графе G. Отсюда следует, что вершины v₀ и v_k — висячие вер­шины в графе G. Тем самым доказано, что всякий граф, удовле­творяющий условию 2. содержит хотя бы две висячие вершины.

Докажем теперь пункт 3 индукцией по n. Равенство m = n-1 для n=2 очевидно верно. Пусть равенство m = n-1 верно для графов, у которых n = r. Докажем это равенство в случае n = r+1. Пусть v — висячая вершина графа G, и e={v ,w} — единственное ребро, инцидентное v. Удалим вершину v и ребро e из графа, т.е. рассмотрим граф G' = (V\{v), Е\{е}). Граф G', очевидно, также удовлетворяет условию 2, и количество вершин в нем равно r. По предположению индукции в графе G' имеется ровно r-1 ребро. Следовательно, исходный граф содержит r+1 вершину и r ребер, т.е. справедливо равенство m = n-1.

3. 4. Заметим, что связность графа не нарушится, если уда­лить любое ребро, входящее в какой-нибудь цикл графа. Предпо­ложим теперь, что граф содержит циклы. Удалим тогда любое ребро, входящее в какой-нибудь цикл. Граф останется связным, и если он вновь содержит циклы, то повторим процедуру удаления ребра, входящего в какой-нибудь цикл. Так будем действовать до тех пор, пока в графе не будут уничтожены все циклы. Поскольку связность при таком удалении ребер не нарушается, то получим дерево. Для деревьев справедливо равенствоm = n-1, так как це­почка утверждений 1. 2.3. уже доказана. Поскольку, по условию, равенствоm = n-1 выполняется с самого начала, значит ни одного ребра мы не удаляли, т.е. граф не содержит циклов.

4. 5. ПустьG имеет k компонент связности G_i = (V_i, ,Е_i), i = l,2,...,k. Тогда все графы G; являются деревьями, и, следова­тельно, для всех i = 1,…,k справедливы равенства m_i = n_i-i. Скла­дывая все эти равенства, получим

m₁ + m₂ +…+ m_k ⁼ n₁ + n₂ +…+n_k – k,

или m = n-k. Однако, по условию, m = n-1. Значит, k=l т.e. G — дерево. Поскольку в дереве между любыми вершинами сущест­вует ровно одна цепь, их соединяющая, то, как легко видеть, до­бавление любого ребра образует ровно один цикл.

5. 1. Ясно, что из условия 5 сразу следует связность графа, т.е.G — дерево. □

Ориентированный граф без контуров называется корневым деревом, если

1. имеется в точности один узел, называемый корнем, в кото­рый не входит ни одна дуга (т.е. степень захода равна нулю);

2. в каждый узел, кроме корня, входит ровно одна дуга;

3. для каждого узла существует путь, начинающийся в корне и заканчивающийся в этом узле.

К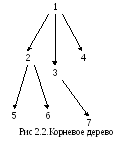орневое дерево обычно изобра­жают корнем вверх, располагая узлы одной глубины на одном уровне. У корневого дерева на рис. 2.2 узел с номером 1 является корнем, узлы 4, 5, 6, 7 —- листья. Высота этого дерева равна 2.

Следующее утверждение является непосредственным следст­вием определения корневого дерева.

Лемма 2.1. Для каждого узла корневого дерева существует в точности один путь, начинающийся в корне и кончающийся в этом узле.

Пусть G - (V,E) — корневое дерево, v,w V. Будем говорить, что узел v является отцом узла w, a w — сыном узла v, если (v,w) Е. Если в G существует путь из v до w, то будем гово­рить, что w — потомок v, a v — предок w. Вершина, не имею­щая сыновей, называется листом. Глубина узла v в корневом дереве — это длина пути из корня в v. При этом глубину корня будем считать равной нулю. Высота узла v — это длина самого длинного пути из v в какой-нибудь лист. Высотой дерева будем называть высоту его корня.

Корневое дерево, каждый узел которого имеет не более двух сыновей, будем называть двоичным деревом. Методом математи­ческой индукции легко доказать следующее утверждение.

Лемма 2.2. Двоичное дерево высоты k содержит не более 2^k листьев.

Специфика дискретных оптимизационных задач практически всегда предполагает, что, как ребра графов, так и дуги орграфов, снабжены некоторой числовой характеристикой. Практический смысл этих характеристик может быть самым разнообразным. Например, в задачах, сформулированных ранее в главе I, это были: длина дороги между соседними городами (задача о кратчай­шем пути), время обработки конкретной детали на конкретном станке (задача оптимального назначения), стоимость проезда из одного города в другой (задача коммивояжера).

Граф (орграф) будем называть взвешенным, если задана функ­ция с: Е→R, иначе говоря, каждому ребру (дуге) из Е поставле­но в соответствие вещественное число с(е). Число с(е) назовем весом ребра (дуги) е. Впрочем, в зависимости от специфики той или иной задачи дискретной оптимизации, число с(е) будем так­же называть стоимостью ребра (дуги) е, или пропускной способ­ностью ребра (дуги) е.

Ориентированный взвешенный граф будем называть сетью. Таким образом, взвешенный граф или сеть задаются тройкой G = (V,E,c).