Глава IV Поиск в графе

Многие алгоритмы на графах основаны на систематическом переборе всех вершин графа, при котором каждая вершина про­сматривается в точности один раз, при этом переход от уже рас­смотренной вершины к еще не рассмотренной вершине осущест­вляется по ребрам графа. В этой главе мы рассмотрим два стан­дартных, широко используемых на практике метода такого пере­бора: поиск в глубину и поиск в ширину. Опишем оба этих мето­да поиска только для неориентированных графов. Модификация этих методов для случая орграфов тривиальна.

§1. Поиск в глубину.

Идея этого метода поиска состоит в следующем. Поиск начи­нается с некоторой фиксированной вершины v, называемой кор­невой вершиной поиска или корнем. При этом считаем v про­смотренной вершиной. Затем выбираем какое-нибудь ребро {v,w}, инцидентное v, проходим его и попадаем в вершину w.

Тот факт, что в процессе поиска использовано именно ребро {v,w} отмечается обычно следующим образом. Ребро {v,w} ори­ентируется из v в w. полученную дугу (v,w) считают дугой кор­невого дерева с корнем v. Такое дерево называется ПВГ-деревом с корнем v, или короче ПВГ(v)—деревом. При переходе от v к w, вершина v объявляется отцом вершины w и обозначается OTEЦ[w], вершина w объявляется просмотренной, и поиск про­должается из вершины w.

В общем случае, когда мы находимся в некоторой вершине v, возникают две возможности:

1. Все вершины, смежные с v, уже просмотрены. В этом слу­чае возвращаемся к вершине ОТЕЦ[v] и продолжаем поиск из нее, а вершину v с этого момента считаем использованной.

2. Существует еще не просмотренная вершина w, смежная с вершиной v. Тогда ребро {v,w} превращаем в дугу (v,w), добав­ляя ее к ПВГ(v)-дереву; полагаем ОТЕЦ[w]=v; проходим по дуге из v в w и продолжаем поиск из w.

Поиск в глубину завершается тогда, когда все вершины графа будут просмотрены. Здесь возможны две ситуации:

1. Корневая вершина использована (т.е. все смежные с ней вершины просмотрены), однако в графе еще есть непросмотрен­ные вершины. В этом случае выбираем произвольную непро­смотренную вершину, объявляем ее корнем и вновь начинаем поиск уже из этой вершины. Такая ситуация возникает только в случае несвязного графа.

2. Корневая вершина и все другие использованы. Поиск на этом заканчивается.

Представим формальное описание изложенного алгоритма. Массив МЕТКА, используемый в алгоритме имеет по одному элементу для каждой вершины графа и служит указателем на то, что просмотрена или нет данная вершина. Считаем, что METKA[v]=0, если v не просмотрена, и METKA[v]=l в против­ном случае. Массив ОТЕЦ описан ранее. Понятно, что он имеет длину n, где n — число вершин в графе. В множестве Т будем хранить дуги ПВГ-деревьев.

Вначале изложим версию алгоритма поиска в глубину, осно­ванную на рекурсивной процедуре ПВГ(v) — поиск в глубину из вершины v. В рассматриваемом алгоритме связность графа не предполагается.

АЛГОРИТМ 4.1. ПОИСК В ГЛУБИНУ

Данные: неориентированный граф G=(V,E), заданный списками смежностей ЗАПИСЬ[v].

Результаты: массив ОТЕЦ, множество Т.

1. procedure ПВГ (v); (*поиск в глубину с корнем v)

2. begin METKA[v]:=1;

3. for w ЗАПИСЬ[v] do

4. if METKA[w]=0 then

5. begin OTEЦ[w]:=v; T:=T{(v,w)};ПВГ(w);

6. end;

7. end;

8. begin (*Главная программа)

T := Ø;

9. for v V do METKA[v]:=0; (*инициализация)

10. for v V do

11. if METKA[v]=0 then

12. begin OTEЦ[v]:=nil; ПВГ(v);

13. end;

14. end.

Н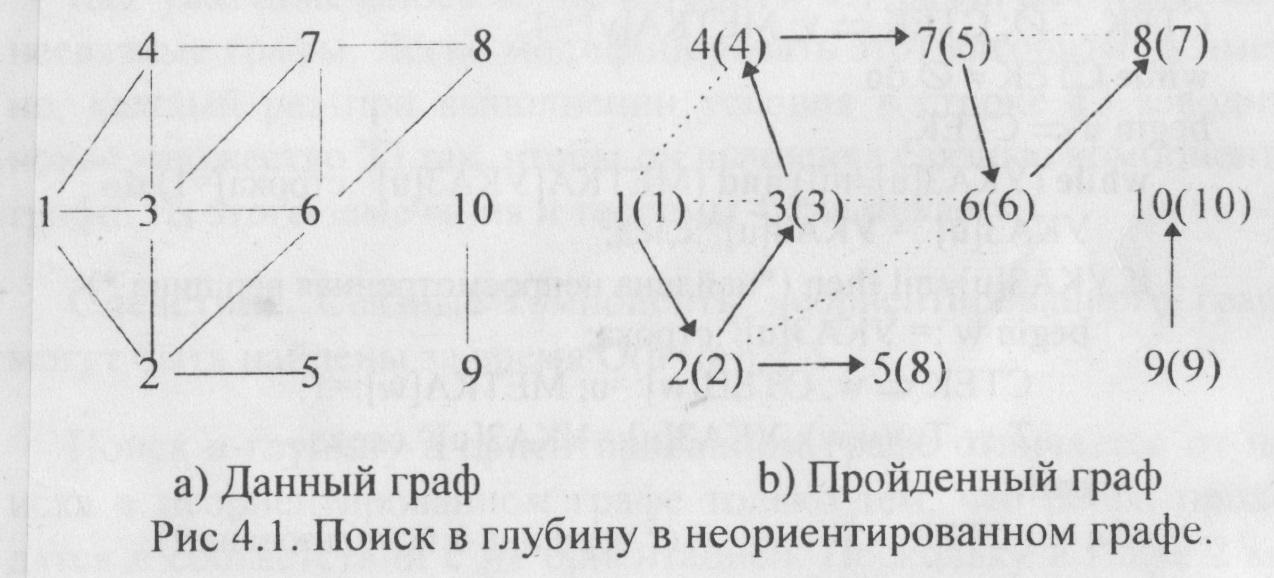а рис.4.1 показано, как поиск в глубину исследует неориен­тированный графG. Предполагается, что в списках смежности этого графа вершины встречаются в порядке возрастания номе­ров, и, что цикл в строках 11-14 алгоритма 4.1 выполнялся в по­рядке возрастания номеров вершин.

В просмотренном графе G дуги ПВГ-деревьев обозначены стрелками в соответствии с ориентацией, полученной в ходе по­иска. Такие дуги часто называют прямыми дугами поиска. Про­чие ребра графа, называемые иногда обратными дугами поиска, обозначены на рисунке пунктирами. Числа в скобках, стоящие у вершин просмотренного графа, соответствуют очередности, в которой они просматривались в ходе поиска. Отметим, что вер­шины с номерами 1, 9 и 11 являются корнями ПВГ-деревьев.

Разберем теперь нерекурсивную версию процедуры ПВГ(v). Рекурсия устраняется стандартным способом с помощью стека. Каждая вершина помещается в стек сразу, как только будет дос­тигнута, то есть просмотрена, и удаляется из стека после того, как будет использована. Поиск новой непросмотренной вершины ведется из той вершины, которая последней попала в стек.

Для организации такого процесса понадобится дополнительно массив указателей УКАЗ длины n, где n=|V|. Предполагается, что в начале работы процедуры поиска выполняются равенства УKA3[v]=HAЧAЛO[v], для всех v из V, иначе говоря, УКАЗ[v] дает адрес первой записи в списке ЗАПИСЬ[v]. В процессе рабо­ты процедуры поиска УКАЗ[v] меняется таким образом, что ука­зывает на следующую запись в списке ЗАПИСЬ[v] после той, ко­торая содержит последнюю просмотренную из нее вершину. Смысл переменных МЕТКА, ОТЕЦ и Т тот же, что и ранее.

1. procedure ПВГ1(v); (* нерекурсивная версия *)

2. begin

3. СТЕК :=Ø; СТЕК v; METKA[v]:=l;

4. while СТЕК ≠ Ø do

5. begin u СТЕК;

6. while (УКАЗ[u] ≠ nil) and (МЕТКА[УКАЗ[u]^.строка]=1) do

7. УКАЗ[u] := УКАЗ[u]^.след;

8. if УКАЗ[u] ≠ nil then (*найдена непросмотренная вершина *)

9. begin w := УКАЗ[u]^.строка:

10. СТЕК w; OTEЦ[w]:=u; METKA[w]:=l;

11. T := T(u,w); УКАЗ[u]:= УКАЗ[u]^.след;

12. end;

13. else СТЕК (* вершина u использована *)

14. end;

15. end.

Теорема 4.1. Сложность алгоритма 4.1 ПОИСК В ГЛУБИНУ есть O(n+m).

Понятно, что цикл в строке 10 (инициализация) требует n операций. Далее, проверка условия, стоящего в строке 13, осуще­ствляется ровно n раз. Вызов процедуры ПВГ(v) влечет за собой просмотр всех вершин связной компоненты графа, содержащей v При этом каждая вершина из связной компоненты просматрива­ется ровно один раз, поскольку просматриваются (т.е, выполня­ется строка 5) только те вершины w, для которых справедливо равенство METKA[w]=0, а сразу после просмотра, в результате вызова ПВГ(w), имеем равенство METKA[w]=l.

В тот момент, когда мы находимся в какой-либо вершине v, для поиска новой, еще не просмотренной вершины w, смежной с v, требуется анализировать ребра, инцидентные v. В процедуре ПВГ1(v) подробно описано, что это можно сделать, используя массив УКАЗ так, что каждое ребро графа анализируется ровно два раза: от v к w и от w к v. Следовательно, при работе алгорит­ма 4.1 анализируются все ребра и все вершины графа, каждое не более двух раз. При каждом анализе количество операций ог­раничено константой. Отсюда сложность алгоритма 4.1 есть O(n+m).

Как уже отмечалось выше алгоритм 4.1 различает связные и несвязные графы. Легко модифицировать этот алгоритм (а имен­но, каждый раз при выполнении условия в строке 13 заводить новое множество Т) так, чтобы он вычислял связные компоненты графа. Из этого замечания и теоремы 4.1 вытекает

Следствие. Связные компоненты неориентированного графа могут быть найдены за время O(n+m).

Поиск в глубину в ориентированном графе отличается от по­иска в неориентированном графе только тем, что ребра прохо­дятся в соответствии с их ориентацией. Поскольку в главе 2 мы условились считать, что в списке ЗАПИСЬ[у] встречаются только те вершины w, для которых (v,w)E, то алгоритм 4.1 корректно работает и в ориентированных графах.