
- •§ 1. Понятие функции двух переменных.
- •§ 2. Частные производные и дифференциалы функции двухпеременных.
- •§ 4. Дифференцирование сложных функций.
- •§ 5. Дифференцирование неявной функции.
- •§ 6. Производная по направлению, градиент.
- •§ 7. Касательная плоскость и нормаль к поверхности.
- •§ 8. Локальный экстремум функции нескольких переменных.
- •§ 9. Условный экстремум функции.
- •§ 10. Найти наибольшее и наименьшее значение функции в замкнутой области.
§ 4. Дифференцирование сложных функций.
Пусть
![]() - функция двух переменных
- функция двух переменных![]() и
и![]() ,
каждая из которых, в свою очередь,
является функцией независимой переменной
,
каждая из которых, в свою очередь,
является функцией независимой переменной![]() ,
то есть
,
то есть![]() .
Тогда
.
Тогда![]() есть сложная функция независимой
переменной
есть сложная функция независимой
переменной![]() .
Если
.
Если![]() дифференцируемы в точке
дифференцируемы в точке![]() ,
а функция
,
а функция![]() дифференцируема в точке
дифференцируема в точке![]() ,
то сложная функция
,
то сложная функция![]() также дифференцируема в точке
также дифференцируема в точке![]() ,
причём
,
причём
![]() (8)
(8)
Аналогично
для функции
![]() ,
,
![]() (9)
(9)
Пример 4.
![]() ,
,
![]()
![]()
![]()
Решение. Используя (8), получаем
![]()
Таким образом,
![]()
Заметим,
что
![]() можно
получить другим способом: сначала
выразить
можно
получить другим способом: сначала
выразить
![]() явно через
явно через![]() ,
затем дифференцировать по
,
затем дифференцировать по![]() .
.
Пусть
теперь
![]() функция двух переменных
функция двух переменных![]() и
и![]() ,
причем
,
причем![]() .
В этом случае имеют место формулы
.
В этом случае имеют место формулы
![]() и
и
![]() (10)
(10)
![]() (11)
(11)
Пример 5. Пусть
![]()
![]()
![]()
Найти
![]()
Решение. Применительно к условию примера соотношения (10) примут вид
![]()


В
общем случае, при дифференцируемости
функции
![]()
![]() переменных, каждая из которых является
дифференцируемой функцией от переменных
переменных, каждая из которых является
дифференцируемой функцией от переменных![]() .
Имеют место формулы
.
Имеют место формулы
![]()
![]() (12)
(12)
Примеры для самостоятельной работы:
Найти:


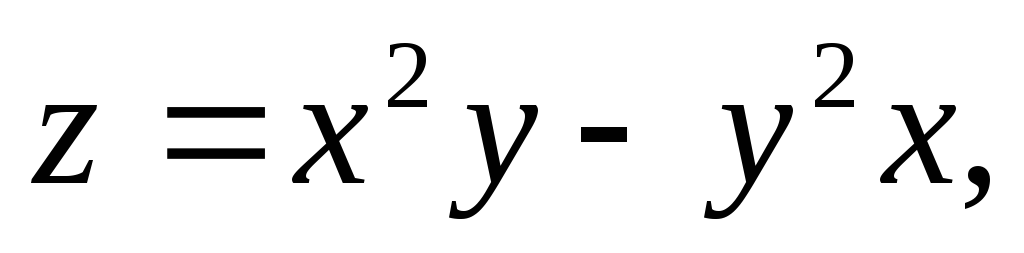
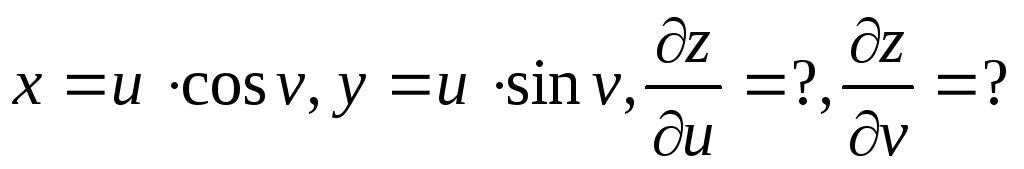



 если
если




 если
если






 если
если














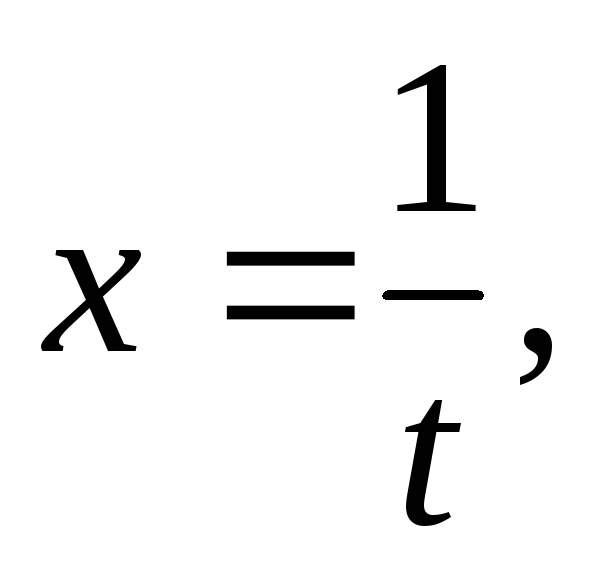


§ 5. Дифференцирование неявной функции.
Пусть
переменные
![]() и
и![]() связаны уравнением:
связаны уравнением:![]() (13)
(13)
Если
каждому значению
![]() из некоторого промежутка отвечает
значение
из некоторого промежутка отвечает
значение![]() ,
при котором выполняется (13), то говорят,
что уравнение (13) определяет функцию
,
при котором выполняется (13), то говорят,
что уравнение (13) определяет функцию![]() ,
заданную неявно.
,
заданную неявно.
Для
нахождения
![]() найдём сначала, по правилу дифференцирования
сложной функции
найдём сначала, по правилу дифференцирования
сложной функции![]() и
и![]() ,
то есть
,
то есть
![]() .
(14)
.
(14)
Откуда,
предполагая, что
![]()
![]() имеем
имеем
![]() .
(15)
.
(15)
Аналогично,
если функция
![]() задана неявно уравнением
задана неявно уравнением![]()
![]()
![]() ,
,
![]() (16)
(16)
Пример 6. Функция
![]() задана уравнением
задана уравнением![]()
Найти![]()
Решение.
Имеем
![]()
Тогда
![]()
![]() Таким образом,
Таким образом,
![]()
Пример 7.
Найти
![]() и
и![]() функции
функции![]() ,
заданной неявно уравнением
,
заданной неявно уравнением![]()
Решение.
Пусть
![]() .
Тогда
.
Тогда
![]()
![]()
Примеры для самостоятельной работы:
Дана
функция
![]() ,
заданная неявно. Найти частные производные
и дифференциалы первого и второго
порядков.
,
заданная неявно. Найти частные производные
и дифференциалы первого и второго
порядков.
§ 6. Производная по направлению, градиент.
Дана
функция
![]() и точка
и точка![]() .
Найти
.
Найти![]() ,
производную
,
производную![]() в
направление вектора
в
направление вектора![]() в
точке
в
точке![]()
Пусть
![]() =
=![]() -единичный
вектор данного направления
-единичный
вектор данного направления
![]() ,
,
![]() -
радиус-вектор точки
-
радиус-вектор точки
![]()
Производная
функции
![]() в точке
в точке![]() по направлению
по направлению![]() определяется соотношением
определяется соотношением
![]()
![]()
![]()
![]() (17)
(17)
Отметим,
что
![]() характеризует
скорость изменения функции
характеризует
скорость изменения функции
![]() в направлении
в направлении![]() .
.
Градиентом
функции
![]() называют вектор
называют вектор![]() ,
координаты которого являются частными
производными функции
,
координаты которого являются частными
производными функции![]() в точке
в точке![]() ,
то есть
,
то есть
![]()
![]()
![]()
![]()
![]() (18)
(18)
Ясно, что
![]()
![]()
![]() (19)
(19)
Пример 8.
Дана функция
![]() .Найти
.Найти
![]()
![]() и
и
![]() в
направление вектора
в
направление вектора
![]() в точке
в точке![]()
Решение.
Найдём направляющие косинусы вектора
![]() .
.
![]()
![]()
![]()
Где
![]() ,
,![]() ,
,![]() -
координаты
-
координаты![]() .
Тогда единичный вектор
.
Тогда единичный вектор![]()
Далее, согласно (18)
![]()
![]() а значит
а значит
![]()
![]()
Таким
образом,
![]()
![]()
![]() =
=![]()
Примеры для самостоятельной работы:
Дана
функция
![]() и точка
и точка![]() .
Найти
.
Найти![]()
![]() ,
,
Производную
![]() в
направление вектора
в
направление вектора
![]() в точке
в точке![]() .
.









 -
выбрать так, чтобы
-
выбрать так, чтобы
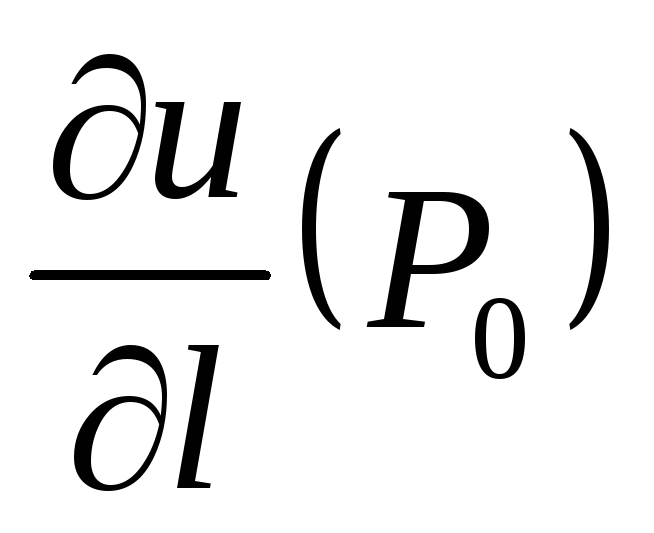 была наименьшей.
была наименьшей.
 -
выбрать так, чтобы
-
выбрать так, чтобы
 была наибольшей.
была наибольшей.









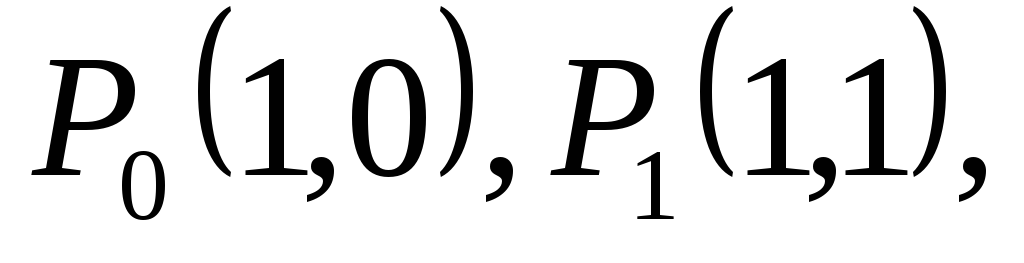

Ответы: 6.1
![]()
![]() ,
,![]() .6.2
.6.2
![]()
![]() ,
,![]() .
6.3
.
6.3![]()
![]() ,
,![]() .
6.4
.
6.4![]()
![]() ,
,![]() .6.5
.6.5
![]()
![]() ,
,![]() .6.6
.6.6
![]()
![]() ,
,![]() .6.7
.6.7
![]()
![]() ,
,![]() .6.8
.6.8
![]()
![]() ,
,![]() .6.9
.6.9
![]()
![]() ,
,![]() .6.10
.6.10
![]()
![]() ,
,![]() .6.11
.6.11
![]()
![]() ,
,![]() .
.
