
- •§ 1. Понятие функции двух переменных.
- •§ 2. Частные производные и дифференциалы функции двухпеременных.
- •§ 4. Дифференцирование сложных функций.
- •§ 5. Дифференцирование неявной функции.
- •§ 6. Производная по направлению, градиент.
- •§ 7. Касательная плоскость и нормаль к поверхности.
- •§ 8. Локальный экстремум функции нескольких переменных.
- •§ 9. Условный экстремум функции.
- •§ 10. Найти наибольшее и наименьшее значение функции в замкнутой области.
§ 9. Условный экстремум функции.
Функция
![]() имеет
условный максимум (минимум) в точке,
имеет
условный максимум (минимум) в точке,![]() если существует такая окрестность
точки
если существует такая окрестность
точки![]() для всех точек которой, удовлетворяющих
уравнениям связи
для всех точек которой, удовлетворяющих
уравнениям связи![]()
![]() выполняется неравенство
выполняется неравенство![]()
![]() .
.
Исследование функции на условный экстремум сводят к исследованию на обычный экстремум функции Лагранжа
![]()
![]()
Константы
![]() называют множителями Лагранжа.
называют множителями Лагранжа.
Необходимые условия условного экстремума выражаются системой
 (25)
(25)
Решение
системы (25)
![]() даёт координаты точки
даёт координаты точки![]() (или системы точек), в которой возможен
условный экстремум.
(или системы точек), в которой возможен
условный экстремум.
Достаточные
условия условного экстремума вытекают
из исследования на знак
![]()
![]() при условии, что дифференциалы
при условии, что дифференциалы![]() удовлетворяют уравнениям
удовлетворяют уравнениям

![]()
![]() (26)
(26)
Точнее
говоря, функция
![]() имеет условный максимум (минимум) в
точке
имеет условный максимум (минимум) в
точке![]() ,
если для всевозможных наборов
,
если для всевозможных наборов![]() ,
удовлетворяющих (26), выполняется
неравенство
,
удовлетворяющих (26), выполняется
неравенство
![]()
![]() (
(![]()
![]() )
)
Пример 13.
Найти условный экстремум функции
![]() при условии
при условии![]()
Решение: Составим функцию Лагранжа
![]()
Имеем

Система имеет два решения
![]()


Далее
![]()
![]()
![]()
![]()
При
![]()
![]() поэтому функция
поэтому функция![]() в точке
в точке![]() имеет условный минимум, а при,
имеет условный минимум, а при,![]()
![]() следовательно,
функция
следовательно,
функция![]() имеет в точке
имеет в точке![]() условный максимум.
условный максимум.
Пример 14.
Найти условные экстремумы функции
![]() при наличии ограничения
при наличии ограничения![]()
Решение: Построим функцию Лагранжа
![]()
Стационарные точки определим из системы
 (27)
(27)
Умножим
первое уравнение на
![]() ,
а второе – на
,
а второе – на![]() .
После вычитания получим
.
После вычитания получим
![]() (28)
(28)
Если
![]() ,
то из первых двух уравнений системы
,
то из первых двух уравнений системы![]() .
Но такие значения переменных
.
Но такие значения переменных![]() и
и![]() не удовлетворяют уравнению связи.
Значит
не удовлетворяют уравнению связи.
Значит![]() и так как
и так как
![]() то из (27) имеем
то из (27) имеем
![]() .
Подставляя это в уравнение связи,
получаем:
.
Подставляя это в уравнение связи,
получаем:![]() откуда
откуда![]() .
Таким образом, из (27)
.
Таким образом, из (27)
![]() .
.
Итак,
единственная стационарная точка функции
Лагранжа.
![]()
Далее,
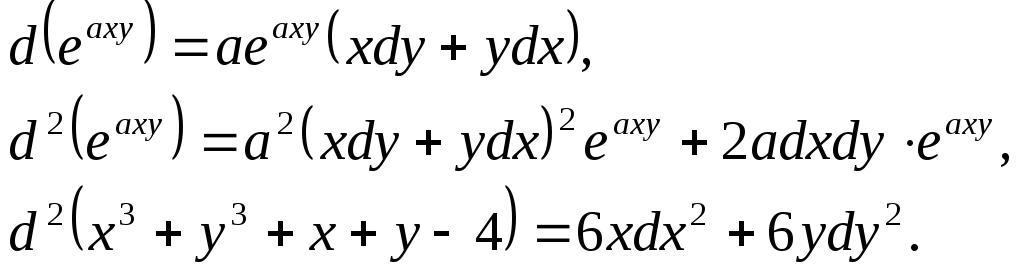
Тогда
для
![]() при
при
![]()
![]()
Получаем
![]()
Из
уравнения связи при
![]() находим соотношение для дифференциалов
находим соотношение для дифференциалов![]() и
и![]() ,
,![]() .
.
Подставляя
![]() в(28),
получаем равенство
в(28),
получаем равенство
![]()
Поэтому,
при
![]() в точке
в точке![]() функция имеет условный максимум, а при
функция имеет условный максимум, а при![]() – условный минимум. Экстремальное
значение равно
– условный минимум. Экстремальное
значение равно
![]() .
.
Примеры для самостоятельной работы:
Найти условный экстремум функции.
Ответы: 9.1![]() .
9.2
.
9.2![]() .
9.3
.
9.3![]()
![]() 9.4
9.4![]()
![]() .
9.5
.
9.5![]() седловая
точка,
седловая
точка,
![]() .
9.6
.
9.6![]()
![]()
![]()
9.7![]()
§ 10. Найти наибольшее и наименьшее значение функции в замкнутой области.
Для того чтобы найти наибольшее и наименьшее значение функции необходимо найти стационарные точки внутри области, вычислить значения функции в этих точках и сравнить с верхней и нижней гранью на границе области.
Пример 15.
![]()
![]()
Решение:
Функция
![]() непрерывна в замкнутом круге
непрерывна в замкнутом круге![]() .
Поэтому, согласно теореме Вейерштрасса,
она на этом множестве достигает своих,
наибольшего и наименьшего, значений
функции.
.
Поэтому, согласно теореме Вейерштрасса,
она на этом множестве достигает своих,
наибольшего и наименьшего, значений
функции.
Система

имеет
решение
![]() .
Так как
.
Так как![]() то в круге
то в круге![]() решений нет. Поэтому экстремум достигается
на границе круга
решений нет. Поэтому экстремум достигается
на границе круга![]()
Составим функцию Лагранжа
![]()
Для определения точек локального экстремума функции Лагранжа решим систему уравнений

Итак, находим две точки возможного экстремума
![]()
![]()
Вычислим значения функции в этих точках
![]()
![]()
Следовательно,
![]()
![]()
![]() Примеры для
самостоятельной работы:
Примеры для
самостоятельной работы:
Найти наибольшее и наименьшее значение функции в области D.
