
- •§ 1. Понятие функции двух переменных.
- •§ 2. Частные производные и дифференциалы функции двухпеременных.
- •§ 4. Дифференцирование сложных функций.
- •§ 5. Дифференцирование неявной функции.
- •§ 6. Производная по направлению, градиент.
- •§ 7. Касательная плоскость и нормаль к поверхности.
- •§ 8. Локальный экстремум функции нескольких переменных.
- •§ 9. Условный экстремум функции.
- •§ 10. Найти наибольшее и наименьшее значение функции в замкнутой области.
§ 7. Касательная плоскость и нормаль к поверхности.
Касательная
плоскость к поверхности
в её точке
![]() (точка касания) есть плоскость, проходящая
через
(точка касания) есть плоскость, проходящая
через![]() ,
которая содержит в себе все касательные,
проведённые в точке
,
которая содержит в себе все касательные,
проведённые в точке![]() к всевозможным кривым, проведённым на
поверхности через точку
к всевозможным кривым, проведённым на
поверхности через точку![]() .
.
Нормалью
к поверхности,
проведенной в точке
![]() ,
называется прямая проходящая через
точку
,
называется прямая проходящая через
точку![]() и перпендикулярная к касательной
плоскости, проведённой в этой точке.
и перпендикулярная к касательной
плоскости, проведённой в этой точке.
Если
уравнение поверхности имеет вид:
![]() то уравнение касательной плоскости в
точке
то уравнение касательной плоскости в
точке![]() имеет вид:
имеет вид:
![]()
![]()
![]() (20)
(20)
Уравнение
нормали к этой поверхности в точке
![]() есть
есть
![]()
![]()
![]() (21)
(21)
В
случае явного задания поверхности
![]() уравнения (20) и (21) примут вид
уравнения (20) и (21) примут вид
![]()
(22)
![]()
![]()
![]()
Пример 9.
Найти
уравнение касательной плоскости и
уравнение нормали к поверхности
![]() в точке
в точке![]()
Решение:
Имеем
![]()
![]()
Тогда,
согласно (22) уравнение касательной
плоскости к данной поверхности в
указанной точке будет иметь вид:
![]() то есть
то есть![]() ,
а уравнение нормали
,
а уравнение нормали
![]()
Пример 10. Найти уравнение касательной плоскости и нормали к поверхности
![]() в точке
в точке![]()
Решение. Имеем
![]()
Тогда
![]()
![]()
![]()
Уравнение касательной плоскости запишем в виде
![]() или,
или,![]() а уравнение нормали
а уравнение нормали

Примеры для самостоятельной работы:
Дано
уравнение поверхность
![]() .
Составить уравнение касательной
плоскости и нормали к данной поверхности
в точке
.
Составить уравнение касательной
плоскости и нормали к данной поверхности
в точке![]() .
.
Ответы: 7.1
§ 8. Локальный экстремум функции нескольких переменных.
Функция
![]() имеет в точке
имеет в точке![]() локальный
максимум (минимум),
если существует такая окрестность
точки
локальный
максимум (минимум),
если существует такая окрестность
точки
![]() ,
для всех точек
,
для всех точек![]() которой, отличных от точки
которой, отличных от точки![]() ,
выполняется неравенство
,
выполняется неравенство![]()
![]() .
.
Необходимое условие экстремума:
Если
дифференцируемая функция
![]() достигает экстремума в точке
достигает экстремума в точке![]() ,
то
,
то
![]() (23)
(23)
или
![]() для всех
для всех![]() (24)
(24)
Точки, в которых выполняется (24), называют стационарными.
Достаточное условие экстремума:
Пусть
![]() - стационарная точка функции. Предположим,
что функция
- стационарная точка функции. Предположим,
что функция![]() дважды непрерывно дифференцируема в
окрестности точки
дважды непрерывно дифференцируема в
окрестности точки![]() и
и![]() значение второго дифференциала в точке
значение второго дифференциала в точке![]() ,
то есть
,
то есть
![]() =
=![]()
Легко
заметить, что
![]() является квадратичной формой относительно
является квадратичной формой относительно![]()
Тогда:
Если
 ,
как функция
,
как функция имеет постоянный знак при всевозможных
наборах
имеет постоянный знак при всевозможных
наборах ,
значений не равных нулю одновременно,
то функция имеет в точке
,
значений не равных нулю одновременно,
то функция имеет в точке экстремум, а именно максимум, при
экстремум, а именно максимум, при и минимум при
и минимум при
Если
 является знакопеременной функцией
является знакопеременной функцией ,
то есть принимает как положительные,
так и отрицательные значения, то точка
,
то есть принимает как положительные,
так и отрицательные значения, то точка не является точкой экстремума.
не является точкой экстремума.Если
 или
или ,
причём существуют такие
,
причём существуют такие ,
при которых
,
при которых ,
то функция
,
то функция в точке
в точке может иметь экстремум, а может и не
иметь. В этом случае необходимо провести
дополнительные исследования.
может иметь экстремум, а может и не
иметь. В этом случае необходимо провести
дополнительные исследования.
Что бы выяснить будет ли квадратичная форма
![]() =
=![]()
знакопостоянной, применяют критерий Сильвестра.
Положим,
![]()
![]()

Для того чтобы
 была знакоположительна, то есть
была знакоположительна, то есть при любых наборах
при любых наборах необходимо и достаточно, чтобы
выполнялись неравенства
необходимо и достаточно, чтобы
выполнялись неравенства
Для того чтобы
 была знакоотрицательна, то есть
была знакоотрицательна, то есть при любых наборах
при любых наборах необходимо и достаточно, чтобы знаки
чисел
необходимо и достаточно, чтобы знаки
чисел чередовались, причём
чередовались, причём
Применим
критерий Сильвестра, для случая функции
двух переменных
![]() .
Положим
.
Положим
![]()
![]()
![]()
![]()
Тогда:
Если
 ,то
функция
,то
функция
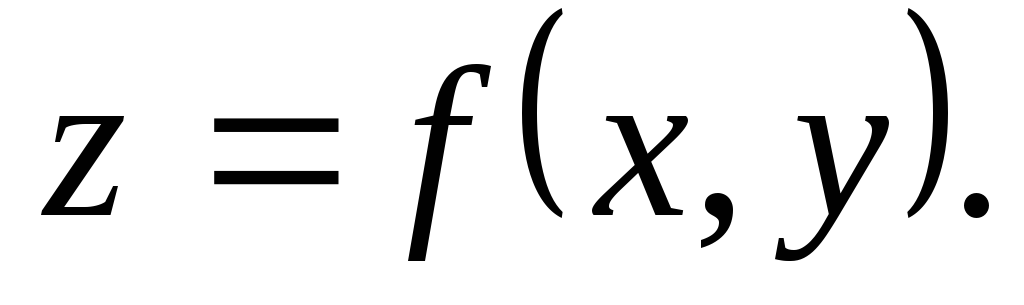 имеет в точке
имеет в точке экстремум, а именно максимум при
экстремум, а именно максимум при
 и минимум при
и минимум при
 .
.Если
 ,
тофункция
,
тофункция
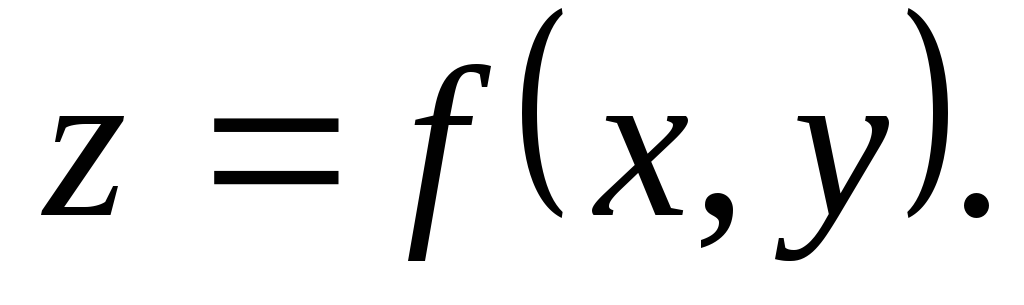 в точке экстремума
в точке экстремума не имеет.
не имеет.Если
 ,то
для решения вопроса об экстремуме в
точке
,то
для решения вопроса об экстремуме в
точке
 требуется дополнительное исследование.
требуется дополнительное исследование.
Пример 11. Исследовать на экстремум функции
![]()
![]()
![]()
![]() .
.
Решение. а) Определим стационарные точки из системы

Откуда
имеем единственную стационарную точку:
![]() Воспользуемся достаточным условием
Воспользуемся достаточным условием
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом,
![]() ,
,
![]() ,
, ,
,
то
есть, согласно критерию Сильвестра,
![]() представляет собой положительно
определённую квадратичную форму.
Следовательно, в точке
представляет собой положительно
определённую квадратичную форму.
Следовательно, в точке![]() функция имеет минимум.
функция имеет минимум.
![]()
![]() Находим,
Находим,
![]()
![]()
Стационарные точки определяются из системы
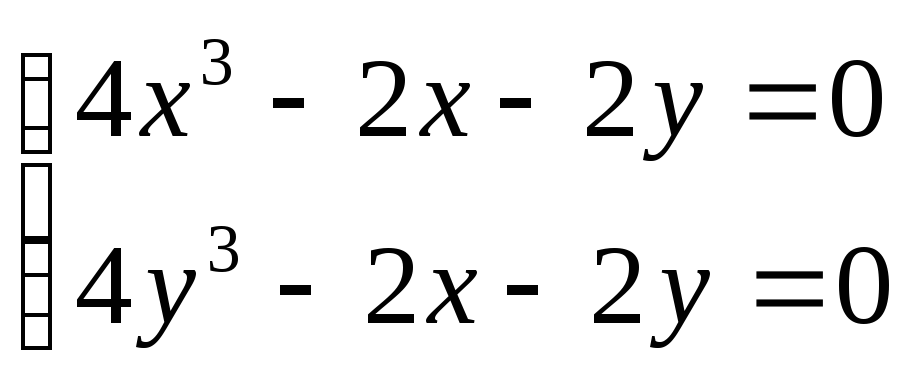
Она
имеет три решения
![]() ,
,![]() ,
,![]() .
Для применения достаточных условий
локального экстремума вычислим вторые
производные
.
Для применения достаточных условий
локального экстремума вычислим вторые
производные
![]()
![]()
![]()
Составим
выражение
![]() .
В точке
.
В точке![]() ,
,![]() следовательно, необходимы дополнительные
исследования.
следовательно, необходимы дополнительные
исследования.
Рассмотрим
![]()
При
![]()
![]() имеем
имеем![]()
При
![]()
![]() имеем
имеем![]() Таким образом, приращение
Таким образом, приращение![]() принимает значения разных знаков, а
поэтому в точке
принимает значения разных знаков, а
поэтому в точке![]() экстремума нет. Далее в точках
экстремума нет. Далее в точках![]() ,
,![]()
![]() и так как
и так как![]() то в этих точках достигается минимум,
причём
то в этих точках достигается минимум,
причём
![]()
Пример 12.
На плоскости даны
![]() точек,
точек,![]()
![]() в которых сосредоточенны массы
в которых сосредоточенны массы![]() .
Требуется найти на этой плоскости точку
.
Требуется найти на этой плоскости точку![]() такую, относительно которой момент
инерции указанной системы материальных
точек минимален.
такую, относительно которой момент
инерции указанной системы материальных
точек минимален.
Решение. Момент инерции относительно точек равен
![]() .
.
Таким
образом, задача сводится к отысканию
точки
![]() ,
в которой функция
,
в которой функция
![]() достигает
своего минимума.
достигает
своего минимума.
Имеем
![]()
![]()
откуда единственной стационарной точкой будет точка с координатами


Далее, так как
![]() B=
B=![]() C=
C=![]() то
то
![]()
и
значит, функция
![]() имеет
в точке
имеет
в точке
![]() локальный минимум.
локальный минимум.
Нетрудно
увидеть, что значение функции
![]() в
этой точке является минимальным.
в
этой точке является минимальным.
Примеры для самостоятельной работы:
Исследовать функцию на экстремум.

 .
.
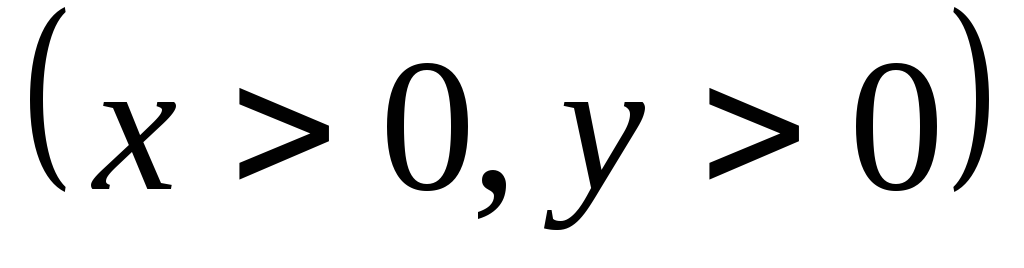










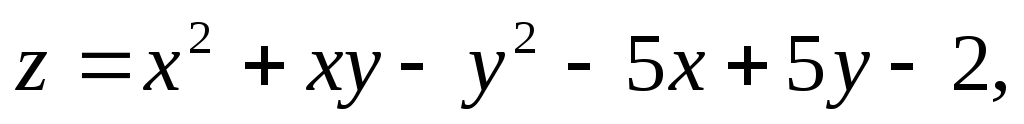


Ответы: 8.1![]() .8.2
.8.2
![]() - седловая точка. 8.3
- седловая точка. 8.3![]() .8.4
.8.4
![]() - седловые точки.8.5
- седловые точки.8.5![]() .
8.6
.
8.6![]() .
8.7
.
8.7![]() .
.
