
- •«Уральский федеральный университет имени первого Президента России б.Н.Ельцина»
- •Методические указания к курсовой работе по теоретической механике
- •Описание курсовой работы
- •Требования к оформлению курсовой работы
- •Этапы выполнения курсовой работы
- •График выполнения курсовой работы
- •Требования к защите курсовой работы
- •Рекомендуемые источники
- •Пример выполнения курсовой работы
- •Вариант 21100000 Динамика кулисного механизма
- •1. Кинематический анализ механизма.
- •1.1. Определение кинематических характеристик
- •1.2. Уравнения геометрических связей
- •3.2. Определение силы, приводящей в движение кулису
- •Курсовая работа
- •«Уральский федеральный университет имени первого Президента России б.Н.Ельцина »
1.2. Уравнения геометрических связей
Как и раньше, начало
координат помещаем в точку
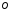 ,
ось
,
ось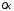 направляем вправо, ось
направляем вправо, ось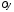 – вверх.
– вверх.
Уравнения связей:
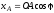 ,
,
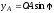 ,
, ,
, ,
,
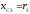 ,
,
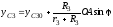 ,
,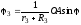 .
.
Последние два соотношения получены интегрированием равенств
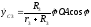 и
и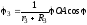 .
.
2. Определение угловой скорости и углового ускорения маховика.
2.1. Кинетическая энергия системы
Кинетическую энергию механизма находим как сумму кинетических энергий его звеньев
 .
.
Кинетическая энергия вращающегося маховика:
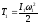 ,
,
 –момент инерции
маховика относительно оси вращения.
–момент инерции
маховика относительно оси вращения.
Кинетическая энергия поступательно движущейся кулисы:
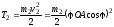 ,
,
Кинетическая энергия катка, совершающего плоское движение:
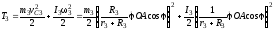 ,
,
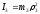 –момент инерции
катка относительно оси, проходящей
через его центр масс.
–момент инерции
катка относительно оси, проходящей
через его центр масс.
Кинетическая энергия системы:
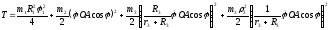 .
.
После тождественных преобразований:
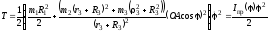
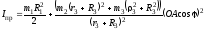
– приведенный к ведущему звену момент инерции.
2.2. Производная кинетической энергии по времени
Производную кинетической энергии по времени находим по правилу вычисления производной произведения и производной сложной функции
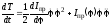 .
.
Здесь
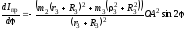
2.3. Элементарная работа и мощность внешних сил и работа внешних сил на конечном перемещении (механизм в горизонтальной плоскости)
В
случае, когда механизм расположен в
горизонтальной плоскости, работу
совершает только вращающий момент
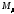 .
Элементарная работа при этом определяется
равенством
.
Элементарная работа при этом определяется
равенством
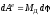 .
.
Мощность
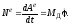
Работа
при повороте маховика на угол
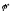
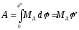 .
.
2.4. Определение угловой скорости маховика при его повороте на угол φ*
Для определения угловой скорости маховика применяем теорему об изменении кинетической энергии в конечной форме, полагая, что механизм в начальный момент находился в покое.
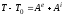 ,
,
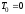 ,
,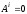 .
.
Подстановка
в это равенство найденных выражений
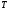 и
и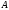 дает
дает
 ,
,
где
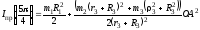 .
.
Тогда
 .
.
2.5. Определение углового ускорения маховика при его повороте на угол φ*
Воспользуемся теоремой об изменении кинетической энергией в дифференциальной форме
 ,
,
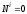 .
.
Подставляя в это уравнение найденные выше значения, находим
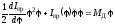 .
.
Откуда
 (1)
(1)
и

Это дифференциальное уравнение второго порядка описывает движение кулисного механизма. Оно может быть проинтегрировано только численно, а также использовано для нахождения углового ускорения маховика в произвольном его положении.
Определим
угловое ускорение маховика при угле
его поворота
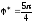 .
.
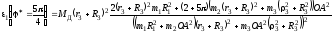 .
.
3. Определение сил
3.1. Определение реакций подшипника и кулисы в положении φ*
Определим реакцию подшипника на оси маховика и силу, приводящую в движение кулису с помощью принципа д`Аламбера, рассматривая движение маховика отдельно от других тел системы.
Маховик
совершает вращательное движении.
Внешними силами, помимо пары сил с
моментом
 ,на него действуют
реакция подшипника
,на него действуют
реакция подшипника
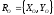 и реакция кулисы
и реакция кулисы (рис.3). Система сил инерции приводится
к паре с моментом
(рис.3). Система сил инерции приводится
к паре с моментом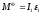 ,
направленным против вращения, т.к. оно
ускоренное (рис.3).
,
направленным против вращения, т.к. оно
ускоренное (рис.3).

Рис.3
Записывая условие уравновешенности плоской системы внешних сил
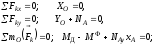
находим
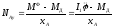 .
.
При
угле
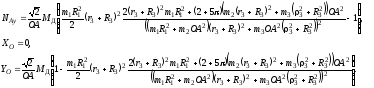
3.2. Определение силы, приводящей в движение кулису
Сила
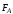 ,
приводящая в движение кулису, по третьему
закону динамики равна реакции кулисы
и направлена в противоположную сторону.
,
приводящая в движение кулису, по третьему
закону динамики равна реакции кулисы
и направлена в противоположную сторону.
Таблица 2.
|
|
|
Н |
|
Н |
|
9,53 |
32,96 |
347,18 |
0 |
347,18 |
ПРИЛОЖЕНИЕ 1
Министерство образования и науки Российской Федерации
ФГАОУ ВПО «Уральский федеральный университет
имени первого Президента России Б.Н.Ельцина»
кафедра теоретической механики

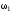 ,
рад/с
,
рад/с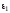 ,
рад/с2
,
рад/с2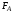 ,
,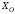 ,
Н
,
Н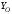 ,
,